Posts published in “Graph”

花花酱 LeetCode 785. Is Graph Bipartite?

By zxi on July 24, 2018

Video is for 花花酱 LeetCode 886. Possible Bipartition, but the algorithm is exact the same.

Problem

https://leetcode.com/problems/is-graph-bipartite/

Given an undirected graph, return true if and only if it is bipartite.

Recall that a graph is bipartite if we can split it’s set of nodes into two independent subsets A and B such that every edge in the graph has one node in A and another node in B.

The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn’t contain any element twice.

Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation: 
The graph looks like this:
0----1
|    |
|    |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.

Example 2:
Input: [[1,2,3], [0,2], [0,1,3], [0,2]]
Output: false
Explanation: 
The graph looks like this:
0----1
| \  |
|  \ |
3----2
We cannot find a way to divide the set of nodes into two independent subsets.

Note:

graph will have length in range [1, 100].
graph[i] will contain integers in range [0, graph.length - 1].
graph[i] will not contain i or duplicate values.
The graph is undirected: if any element j is in graph[i], then i will be in graph[j].

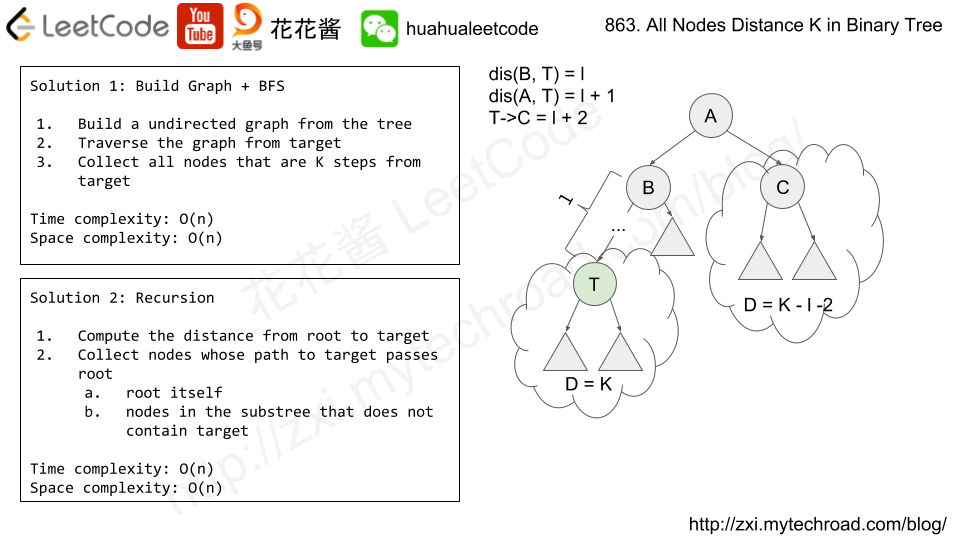
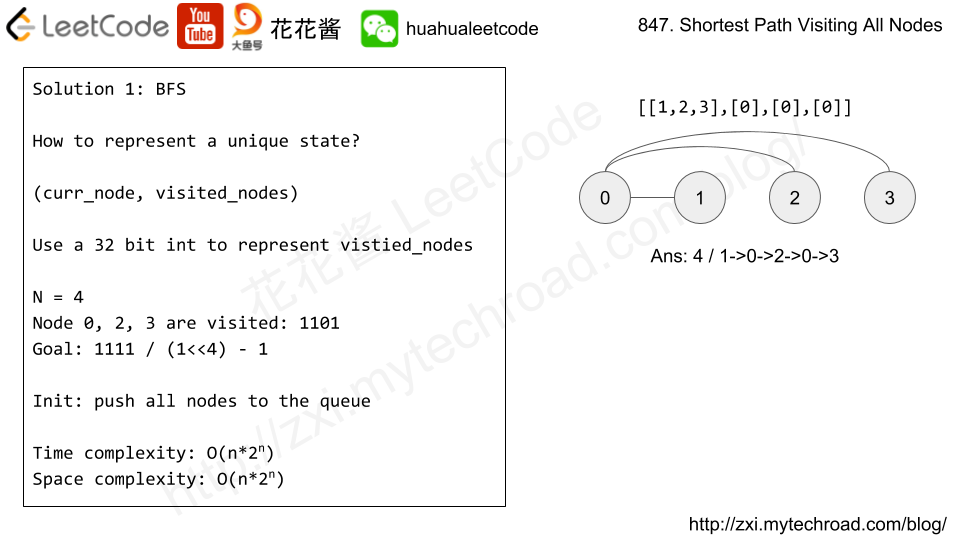
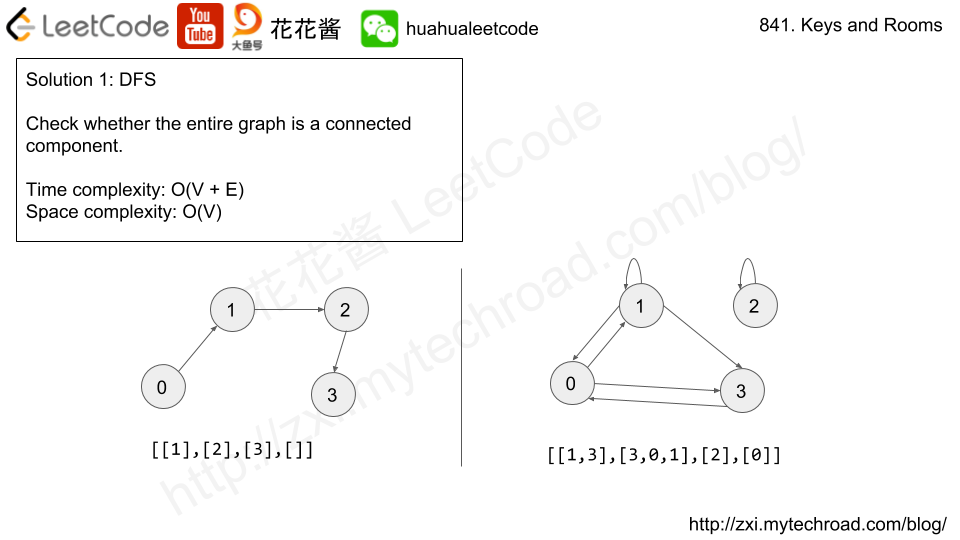
Solution: Graph Coloring

For each node

If has not been colored, color it to RED(1).
Color its neighbors with a different color RED(1) to BLUE(-1) or BLUE(-1) to RED(-1).

If we can finish the coloring then the graph is bipartite. All red nodes on the left no connections between them and all blues nodes on the right, again no connections between them. red and blue nodes are neighbors.

Time complexity: O(V+E)

Space complexity: O(V)

C++ / DFS

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

bool isBipartite(vector<vector<int>>& graph) {

const int n = graph.size();

vector<int> colors(n);

for (int i = 0; i < n; ++i)

if (!colors[i] && !coloring(graph, colors, 1, i))

return false;

return true;

}

private:

bool coloring(const vector<vector<int>>& graph, vector<int>& colors, int color, int node) {

if (colors[node]) return colors[node] == color;

colors[node] = color;

for (int nxt : graph[node])

if (!coloring(graph, colors, -color, nxt)) return false;

return true;

}

};

Problem

题目大意：给你一棵二叉树（根结点root）和一个target节点。返回所有到target的距离为K的节点。

We are given a binary tree (with root node root), a target node, and an integer value K.

Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
Output: [7,4,1]
Explanation: 
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.

Note that the inputs "root" and "target" are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.

Note:

The given tree is non-empty.
Each node in the tree has unique values 0 <= node.val <= 500.
The target node is a node in the tree.
0 <= K <= 1000.

Solution1: DFS + BFS

Use DFS to build the graph, and use BFS to find all the nodes that are exact K steps from target.

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {

buildGraph(nullptr, root);

vector<int> ans;

unordered_set<TreeNode*> seen;

queue<TreeNode*> q;

seen.insert(target);

q.push(target);

int k = 0;

while (!q.empty() && k <= K) {

int s = q.size();

while (s--) {

TreeNode* node = q.front(); q.pop();

if (k == K) ans.push_back(node->val);

for (TreeNode* child : g[node]) {

if (seen.count(child)) continue;

q.push(child);

seen.insert(child);

}

++k;

}

return ans;

}

private:

unordered_map<TreeNode*, vector<TreeNode*>> g;

void buildGraph(TreeNode* parent, TreeNode* child) {

if (parent) {

g[parent].push_back(child);

g[child].push_back(parent);

}

if (child->left) buildGraph(child, child->left);

if (child->right) buildGraph(child, child->right);

}

};

Array version

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {

constexpr int kMaxN = 500 + 1;

g = vector<vector<int>>(kMaxN);

buildGraph(nullptr, root);

vector<int> ans;

vector<int> seen(kMaxN);

queue<int> q;

seen[target->val] = 1;

q.push(target->val);

int k = 0;

while (!q.empty() && k <= K) {

int s = q.size();

while (s--) {

int node = q.front(); q.pop();

if (k == K) ans.push_back(node);

for (int child : g[node]) {

if (seen[child]) continue;

q.push(child);

seen[child] = 1;

}

++k;

}

return ans;

}

private:

vector<vector<int>> g;

void buildGraph(TreeNode* parent, TreeNode* child) {

if (parent) {

g[parent->val].push_back(child->val);

g[child->val].push_back(parent->val);

}

if (child->left) buildGraph(child, child->left);

if (child->right) buildGraph(child, child->right);

}

};

Solution 2: Recursion

Recursively compute the distance from root to target, and collect nodes accordingly.

Time complexity: O(n)

Space complexity: O(n)

// Author: Huahua

// Running time: 5 ms

class Solution {

public:

vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {

ans.clear();

dis(root, target, K);

return ans;

}

private:

vector<int> ans;

// Returns the distance from root to target.

// Returns -1 if target does not in the tree.

int dis(TreeNode* root, TreeNode* target, int K) {

if (root == nullptr) return -1;

if (root == target) {

collect(target, K);

return 0;

}

int l = dis(root->left, target, K);

int r = dis(root->right, target, K);

// Target in the left subtree

if (l >= 0) {

if (l == K - 1) ans.push_back(root->val);

// Collect nodes in right subtree with depth K - l - 2

collect(root->right, K - l - 2);

return l + 1;

}

// Target in the right subtree

if (r >= 0) {

if (r == K - 1) ans.push_back(root->val);

// Collect nodes in left subtree with depth K - r - 2

collect(root->left, K - r - 2);

return r + 1;

}

return -1;

}

// Collect nodes that are d steps from root.

void collect(TreeNode* root, int d) {

if (root == nullptr || d < 0) return;

if (d == 0) ans.push_back(root->val);

collect(root->left, d - 1);

collect(root->right, d - 1);

}

};

花花酱 LeetCode 847. Shortest Path Visiting All Nodes

By zxi on June 3, 2018

Problem

题目大意：求顶点覆盖的最短路径。

https://leetcode.com/problems/shortest-path-visiting-all-nodes/description/

An undirected, connected graph of N nodes (labeled 0, 1, 2, ..., N-1) is given as graph.

graph.length = N, and j != i is in the list graph[i] exactly once, if and only if nodes i and j are connected.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

Input: [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

Input: [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Solution: BFS

Time complexity: O(n*2^n)

Space complexity: O(n*2^n)

C++

// Author: Huahua

// Running time: 34 ms

class Solution {

public:

int shortestPathLength(vector<vector<int>>& graph) {

const int kAns = (1 << (graph.size())) - 1;

queue<pair<int, int>> q;

unordered_set<int> visited; // (cur_node << 16) | state

for (int i = 0; i < graph.size(); ++i)

q.push({i, 1 << i});

int steps = 0;

while (!q.empty()) {

int s = q.size();

while (s--) {

auto p = q.front();

q.pop();

int n = p.first;

int state = p.second;

if (state == kAns) return steps;

int key = (n << 16) | state;

if (visited.count(key)) continue;

visited.insert(key);

for (int next : graph[n])

q.push({next, state | (1 << next)});

}

++steps;

}

return -1;

}

};

C++ / vector

// Author: Huahua

// Running time: 10 ms

class Solution {

public:

int shortestPathLength(vector<vector<int>>& graph) {

const int n = graph.size();

const int kAns = (1 << n) - 1;

queue<pair<int, int>> q;

vector<vector<int>> visited(n, vector<int>(1 << n));

for (int i = 0; i < n; ++i)

q.push({i, 1 << i});

int steps = 0;

while (!q.empty()) {

int s = q.size();

while (s--) {

auto p = q.front();

q.pop();

int node = p.first;

int state = p.second;

if (state == kAns) return steps;

if (visited[node][state]) continue;

visited[node][state] = 1;

for (int next : graph[node])

q.push({next, state | (1 << next)});

}

++steps;

}

return -1;

}

};

Problem

There are N rooms and you start in room 0. Each room has a distinct number in 0, 1, 2, ..., N-1, and each room may have some keys to access the next room.

Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, ..., N-1] where N = rooms.length. A key rooms[i][j] = v opens the room with number v.

Initially, all the rooms start locked (except for room 0).

You can walk back and forth between rooms freely.

Return true if and only if you can enter every room.

Example 1:

Input: [[1],[2],[3],[]]
Output: true
Explanation:  
We start in room 0, and pick up key 1.
We then go to room 1, and pick up key 2.
We then go to room 2, and pick up key 3.
We then go to room 3.  Since we were able to go to every room, we return true.

Example 2:

Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can't enter the room with number 2.

Note:

1 <= rooms.length <= 1000
0 <= rooms[i].length <= 1000
The number of keys in all rooms combined is at most 3000.

Solution: DFS

Time complexity: O(V + E)

Space complexity: O(V)

C++

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

bool canVisitAllRooms(vector<vector<int>>& rooms) {

unordered_set<int> visited;

dfs(rooms, 0, visited);

return visited.size() == rooms.size();

}

private:

void dfs(const vector<vector<int>>& rooms,

int cur, unordered_set<int>& visited) {

if (visited.count(cur)) return;

visited.insert(cur);

for (int nxt : rooms[cur])

dfs(rooms, nxt, visited);

}

};

花花酱 LeetCode 827. Making A Large Island

By zxi on April 30, 2018

Problem

In a 2D grid of 0s and 1s, we change at most one 0 to a 1.

After, what is the size of the largest island? (An island is a 4-directionally connected group of 1s).

Example 1:

Input: [[1, 0], [0, 1]]
Output: 3
Explanation: Change one 0 to 1 and connect two 1s, then we get an island with area = 3.

Example 2:

Input: [[1, 1], [1, 0]]
Output: 4
Explanation: Change the 0 to 1 and make the island bigger, only one island with area = 1.

Example 3:

Input: [[1, 1], [1, 1]]
Output: 4
Explanation: Can't change any 0 to 1, only one island with area = 1.

Notes:

1 <= grid.length = grid[0].length <= 50.
0 <= grid[i][j] <= 1.

Solution

Step 1: give each connected component a unique id and count its ara.

Step 2: for each 0 zero, check its 4 neighbours, sum areas up by unique ids.

Time complexity: O(n*m)

Space complexity: O(n*m)

C++

// Author: Huahua

// Running time: 14 ms

class Solution {

public:

int largestIsland(vector<vector<int>>& grid) {

color_ = 1;

g_ = &grid;

m_ = grid.size();

n_ = grid[0].size();

unordered_map<int, int> areas; // color -> area

int ans = 0;

for (int i = 0; i < m_; ++i)

for (int j = 0; j < n_; ++j)

if (grid[i][j] == 1) {

++color_;

areas[color_] = getArea(j, i);

ans = max(ans, areas[color_]);

}

for (int i = 0; i < m_; ++i)

for (int j = 0; j < n_; ++j)

if (grid[i][j] == 0) {

int area = 1;

for (int color : set<int>{getColor(j, i - 1), getColor(j, i + 1),

getColor(j - 1, i), getColor(j + 1, i)})

area += areas[color];

ans = max(ans, area);

}

return ans;

}

private:

int m_;

int n_;

int color_;

vector<vector<int>>* g_; // does not own the object.

int getColor(int x, int y) {

return (x < 0 || x >= n_ || y < 0 || y >= m_) ? 0 : (*g_)[y][x];

}

// Return the area of a connected component, set all elements to color_.

int getArea(int x, int y) {

if (x < 0 || x >= n_ || y < 0 || y >= m_ || (*g_)[y][x] != 1) return 0;

(*g_)[y][x] = color_;

return 1 + getArea(x - 1, y) + getArea(x + 1, y)

+ getArea(x, y - 1) + getArea(x, y + 1);

}

};

Posts published in “Graph”

花花酱 LeetCode 785. Is Graph Bipartite?

Problem

Solution: Graph Coloring

Related Problem

花花酱 LeetCode 863. All Nodes Distance K in Binary Tree

Problem

Solution1: DFS + BFS

Solution 2: Recursion

花花酱 LeetCode 847. Shortest Path Visiting All Nodes

Problem

Solution: BFS

Related Problems

花花酱 LeetCode 841. Keys and Rooms

Problem

Solution: DFS

花花酱 LeetCode 827. Making A Large Island

Problem

Solution