Posts published in “Tree”

花花酱 LeetCode 701. Insert into a Binary Search Tree

By zxi on July 12, 2018

Problem

Given the root node of a binary search tree (BST) and a value to be inserted into the tree, insert the value into the BST. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.

Note that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.

For example,

Given the tree:

/ \

2 7

/ \

1 3

And the value to insert: 5

You can return this binary search tree:

/ \

2 7

/ \ /

1 3 5

This tree is also valid:

/ \

2 7

/ \

1 3

Solution: Recursion

Time complexity: O(logn ~ n)

Space complexity: O(logn ~ n)

// Author: Huahua

// Running time: 52 ms

class Solution {

public:

TreeNode* insertIntoBST(TreeNode* root, int val) {

if (root == nullptr) return new TreeNode(val);

if (val > root->val)

root->right = insertIntoBST(root->right, val);

else

root->left = insertIntoBST(root->left, val);

return root;

}

};

花花酱 LeetCode 700. Search in a Binary Search Tree

By zxi on July 12, 2018

Problem

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node’s value equals the given value. Return the subtree rooted with that node. If such node doesn’t exist, you should return NULL.

For example,

Given the tree:
        4
       / \
      2   7
     / \
    1   3

And the value to search: 2

You should return this subtree:

      2     
     / \   
    1   3

In the example above, if we want to search the value 5, since there is no node with value 5, we should return NULL.

Solution: Recursion

Time complexity: O(logn ~ n)

Space complexity: O(logn ~ n)

// Author: Huahua

// Running time: 24 ms

class Solution {

public:

TreeNode* searchBST(TreeNode* root, int val) {

if (root == nullptr) return nullptr;

if (val == root->val)

return root;

else if (val > root->val)

return searchBST(root->right, val);

return searchBST(root->left, val);

}

};

花花酱 LeetCode 865. Smallest Subtree with all the Deepest Nodes

By zxi on July 8, 2018

Problem

Given a binary tree rooted at root, the depth of each node is the shortest distance to the root.

A node is deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is that node, plus the set of all descendants of that node.

Return the node with the largest depth such that it contains all the deepest nodes in it’s subtree.

Example 1:

Input: [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation:



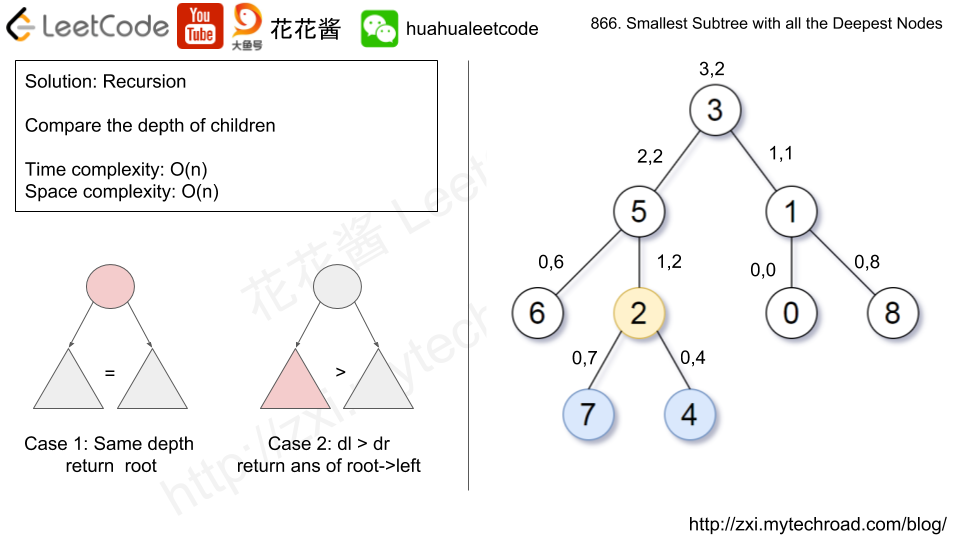
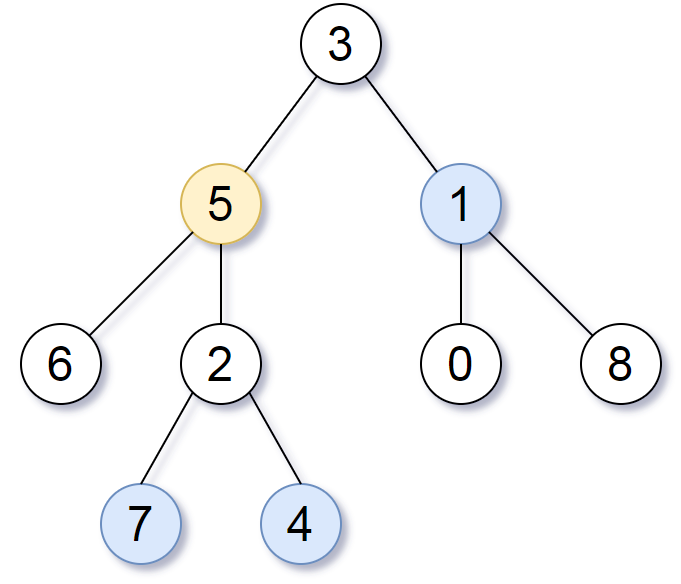
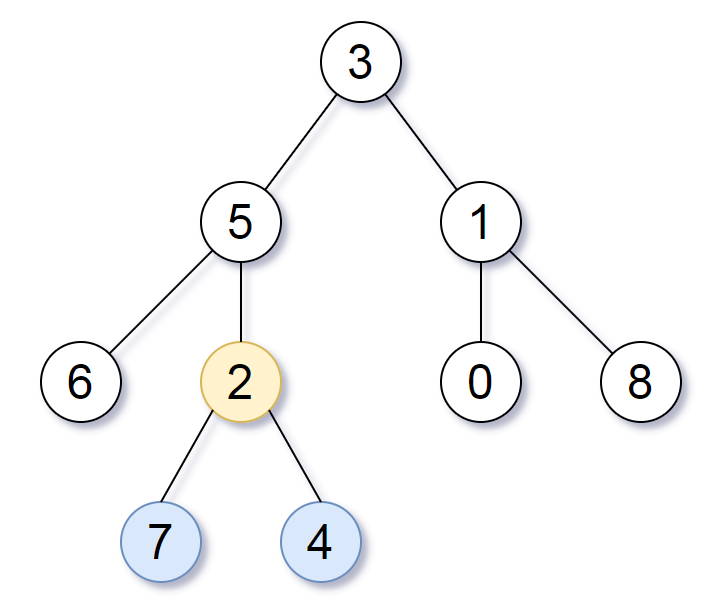We return the node with value 2, colored in yellow in the diagram.
The nodes colored in blue are the deepest nodes of the tree.
The input "[3, 5, 1, 6, 2, 0, 8, null, null, 7, 4]" is a serialization of the given tree.
The output "[2, 7, 4]" is a serialization of the subtree rooted at the node with value 2.
Both the input and output have TreeNode type.

Note:

The number of nodes in the tree will be between 1 and 500.
The values of each node are unique.

Solution: Recursion

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 0 ms

class Solution {

public:

TreeNode* subtreeWithAllDeepest(TreeNode* root) {

return depth(root).second;

}

private:

pair<int, TreeNode*> depth(TreeNode* root) {

if (root == nullptr)

return {-1, nullptr};

auto l = depth(root->left);

auto r = depth(root->right);

int dl = l.first;

int dr = r.first;

return { max(dl, dr) + 1,

dl == dr ? root : (dl > dr) ? l.second : r.second};

}

};

// Author: Huahua

// Running time: 0 ms

class Solution {

public:

TreeNode* subtreeWithAllDeepest(TreeNode* root) {

TreeNode* ans;

depth(root, &ans);

return ans;

}

private:

int depth(TreeNode* root, TreeNode** s) {

if (root == nullptr)

return -1;

TreeNode* sl;

TreeNode* sr;

int l = depth(root->left, &sl);

int r = depth(root->right, &sr);

*s = (l == r) ? root : ((l > r) ? sl : sr);

return max(l, r) + 1;

}

};

Python3

"""

Author: Huahua

Running time: 40 ms

"""

class Solution:

def subtreeWithAllDeepest(self, root):

def solve(root):

if not root: return (-1, None)

dl, sl = solve(root.left)

dr, sr = solve(root.right)

if dl == dr: return (dl + 1, root)

return (dl + 1, sl) if dl > dr else (dr + 1, sr)

return solve(root)[1]

花花酱 LeetCode 863. All Nodes Distance K in Binary Tree

By zxi on June 30, 2018

Problem

题目大意：给你一棵二叉树（根结点root）和一个target节点。返回所有到target的距离为K的节点。

We are given a binary tree (with root node root), a target node, and an integer value K.

Return a list of the values of all nodes that have a distance K from the target node. The answer can be returned in any order.

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
Output: [7,4,1]
Explanation: 
The nodes that are a distance 2 from the target node (with value 5)
have values 7, 4, and 1.

Note that the inputs "root" and "target" are actually TreeNodes.
The descriptions of the inputs above are just serializations of these objects.

Note:

The given tree is non-empty.
Each node in the tree has unique values 0 <= node.val <= 500.
The target node is a node in the tree.
0 <= K <= 1000.

Solution1: DFS + BFS

Use DFS to build the graph, and use BFS to find all the nodes that are exact K steps from target.

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {

buildGraph(nullptr, root);

vector<int> ans;

unordered_set<TreeNode*> seen;

queue<TreeNode*> q;

seen.insert(target);

q.push(target);

int k = 0;

while (!q.empty() && k <= K) {

int s = q.size();

while (s--) {

TreeNode* node = q.front(); q.pop();

if (k == K) ans.push_back(node->val);

for (TreeNode* child : g[node]) {

if (seen.count(child)) continue;

q.push(child);

seen.insert(child);

}

++k;

}

return ans;

}

private:

unordered_map<TreeNode*, vector<TreeNode*>> g;

void buildGraph(TreeNode* parent, TreeNode* child) {

if (parent) {

g[parent].push_back(child);

g[child].push_back(parent);

}

if (child->left) buildGraph(child, child->left);

if (child->right) buildGraph(child, child->right);

}

};

Array version

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {

constexpr int kMaxN = 500 + 1;

g = vector<vector<int>>(kMaxN);

buildGraph(nullptr, root);

vector<int> ans;

vector<int> seen(kMaxN);

queue<int> q;

seen[target->val] = 1;

q.push(target->val);

int k = 0;

while (!q.empty() && k <= K) {

int s = q.size();

while (s--) {

int node = q.front(); q.pop();

if (k == K) ans.push_back(node);

for (int child : g[node]) {

if (seen[child]) continue;

q.push(child);

seen[child] = 1;

}

++k;

}

return ans;

}

private:

vector<vector<int>> g;

void buildGraph(TreeNode* parent, TreeNode* child) {

if (parent) {

g[parent->val].push_back(child->val);

g[child->val].push_back(parent->val);

}

if (child->left) buildGraph(child, child->left);

if (child->right) buildGraph(child, child->right);

}

};

Solution 2: Recursion

Recursively compute the distance from root to target, and collect nodes accordingly.

Time complexity: O(n)

Space complexity: O(n)

// Author: Huahua

// Running time: 5 ms

class Solution {

public:

vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {

ans.clear();

dis(root, target, K);

return ans;

}

private:

vector<int> ans;

// Returns the distance from root to target.

// Returns -1 if target does not in the tree.

int dis(TreeNode* root, TreeNode* target, int K) {

if (root == nullptr) return -1;

if (root == target) {

collect(target, K);

return 0;

}

int l = dis(root->left, target, K);

int r = dis(root->right, target, K);

// Target in the left subtree

if (l >= 0) {

if (l == K - 1) ans.push_back(root->val);

// Collect nodes in right subtree with depth K - l - 2

collect(root->right, K - l - 2);

return l + 1;

}

// Target in the right subtree

if (r >= 0) {

if (r == K - 1) ans.push_back(root->val);

// Collect nodes in left subtree with depth K - r - 2

collect(root->left, K - r - 2);

return r + 1;

}

return -1;

}

// Collect nodes that are d steps from root.

void collect(TreeNode* root, int d) {

if (root == nullptr || d < 0) return;

if (d == 0) ans.push_back(root->val);

collect(root->left, d - 1);

collect(root->right, d - 1);

}

};

花花酱 LeetCode 823. Binary Trees With Factors

By zxi on April 29, 2018

Problem

题目大意：给你一些可以重复使用的数字问能够构成多少种不同的特殊二叉树（根结点的值需为子节点值的乘积）。

https://leetcode.com/problems/binary-trees-with-factors/description/

Given an array of unique integers, each integer is strictly greater than 1.

We make a binary tree using these integers and each number may be used for any number of times.

Each non-leaf node’s value should be equal to the product of the values of it’s children.

How many binary trees can we make? Return the answer modulo 10 ** 9 + 7.

Example 1:

Input: A = [2, 4]
Output: 3 Explanation: We can make these trees: [2], [4], [4, 2, 2]

Example 2:

Input: A = [2, 4, 5, 10]
Output: 7
Explanation: We can make these trees: [2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2].

Note:

1 <= A.length <= 1000.
2 <= A[i] <= 10 ^ 9.

Solution: DP

Use dp[i] to denote the number of valid binary trees using the first i + 1 smallest elements and roots at A[i].

dp[i] = sum(dp[j] * dp[i/j]), 0 <= j < i, A[i] is a factor of A[j] and A[i] / A[j] also in A.

      A[i]
     /    \
 A[j]  (A[i]/A[j])
  / \     / \
 .....   .....

ans = sum(dp[i]), for all possible i.

Time complexity: O(n^2)

Space complexity: O(n^2)

C++

// Author: Huahua

// Running time: 53 ms

class Solution {

public:

int numFactoredBinaryTrees(vector<int>& A) {

constexpr long kMod = 1000000007;

std::sort(A.begin(), A.end());

unordered_map<int, long> dp;

for (int i = 0; i < A.size(); ++i) {

dp[A[i]] = 1;

for (int j = 0; j < i; ++j)

if (A[i] % A[j] == 0 && dp.count(A[i] / A[j]))

dp[A[i]] += (dp[A[j]] * dp[A[i] / A[j]]) % kMod;

}

long ans = 0;

for (const auto& kv : dp)

ans += kv.second;

return ans % kMod;

}

};