Posts published in “Tree”

花花酱 LeetCode 1367. Linked List in Binary Tree

By zxi on March 1, 2020

Given a binary tree root and a linked list with head as the first node.

Return True if all the elements in the linked list starting from the head correspond to some downward path connected in the binary tree otherwise return False.

In this context downward path means a path that starts at some node and goes downwards.

Example 1:

Input: head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
Output: true
Explanation: Nodes in blue form a subpath in the binary Tree.

Example 2:

Input: head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
Output: true

Example 3:

Input: head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
Output: false
Explanation: There is no path in the binary tree that contains all the elements of the linked list from head.

Constraints:

1 <= node.val <= 100 for each node in the linked list and binary tree.
The given linked list will contain between 1 and 100 nodes.
The given binary tree will contain between 1 and 2500 nodes.

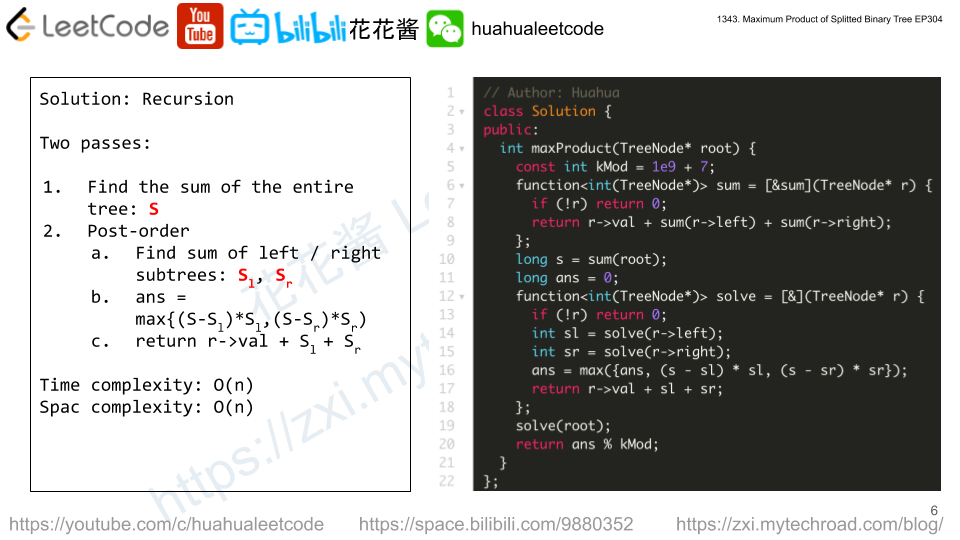
Solution: Recursion

We need two recursion functions: isSubPath / isPath, the later one does a strict match.

Time complexity: O(|L| * |T|)
Space complexity: O(|T|)

C++

class Solution {

public:

bool isSubPath(ListNode* head, TreeNode* root) {

if (!root) return false;

return isPath(head, root) || isSubPath(head, root->left) || isSubPath(head, root->right);

}

private:

bool isPath(ListNode* head, TreeNode* root) {

if (!head) return true;

if (!root) return false;

if (root->val != head->val) return false;

return isPath(head->next, root->left) || isPath(head->next, root->right);

}

};

花花酱 LeetCode 1361. Validate Binary Tree Nodes

By zxi on February 23, 2020

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

Example 1:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Example 4:

Input: n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
Output: false

Constraints:

1 <= n <= 10^4
leftChild.length == rightChild.length == n
-1 <= leftChild[i], rightChild[i] <= n - 1

Solution: Count in-degrees for each node

in degree must <= 1 and there must be exact one node that has 0 in-degree.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {

vector<int> in(n);

for (int l : leftChild) if (l >= 0) ++in[l];

for (int r : rightChild) if (r >= 0) ++in[r];

int zero = 0;

for (int i = 0; i < n; ++i) {

if (in[i] > 1) return false;

if (in[i] == 0) ++zero;

}

// # of nodes without parent must be 1.

return zero == 1;

}

};

花花酱 LeetCode 108. Convert Sorted Array to Binary Search Tree

By zxi on February 2, 2020

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

Solution: Recursion

Recursively build a BST for a given range.

def build(nums, l, r):
if l > r: return None
m = l + (r – l) / 2
root = TreeNode(nums[m])
root.left = build(nums, l, m – 1)
root.right = build(nums, m + 1, r)
return root

return build(nums, 0, len(nums) – 1)

Time complexity: O(n)
Space complexity: O(logn)

C++

// Author: Huahua

class Solution {

public:

TreeNode* sortedArrayToBST(vector<int>& nums) {

function<TreeNode*(int l, int r)> build = [&](int l, int r) {

if (l > r) return static_cast<TreeNode*>(nullptr);

int m = l + (r - l) / 2;

TreeNode* root = new TreeNode(nums[m]);

root->left = build(l, m - 1);

root->right = build(m + 1, r);

return root;

};

return build(0, nums.size() - 1);

}

};

Java

// Author: Huahua

class Solution {

public TreeNode sortedArrayToBST(int[] nums) {

return buildBST(nums, 0, nums.length - 1);

}

private TreeNode buildBST(int[] nums, int l, int r) {

if (l > r) return null;

int m = l + (r - l) / 2;

TreeNode root = new TreeNode(nums[m]);

root.left = buildBST(nums, l, m - 1);

root.right = buildBST(nums, m + 1, r);

return root;

}

Python3

# Author: Huahua

class Solution:

def sortedArrayToBST(self, nums: List[int]) -> TreeNode:

def buildBST(l: int, r: int) -> TreeNode:

if l > r: return None

m = l + (r - l) // 2

root = TreeNode(nums[m])

root.left = buildBST(l, m - 1)

root.right = buildBST(m + 1, r)

return root

return buildBST(0, len(nums) - 1)

JavaScript

// Author: Huahua

var sortedArrayToBST = function(nums) {

var buildBST = function(l, r) {

if (l > r) return null;

let m = l + Math.floor((r - l) / 2);

let root = new TreeNode(nums[m]);

root.left = buildBST(l, m - 1);

root.right = buildBST(m + 1, r);

return root;

}

return buildBST(0, nums.length - 1);

};

花花酱 LeetCode 1339. Maximum Product of Splitted Binary Tree

By zxi on February 1, 2020

Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation:  Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

Constraints:

Each tree has at most 50000 nodes and at least 2 nodes.
Each node’s value is between [1, 10000].

Solution: Recursion

Two passes:
First pass, compute the sum of the entire tree S.
Second pass, for each node, compute the sum of left/right subtree S_l, S_r.
ans = max{(S – S_l) * S_l, (S – S_r) * S_r}

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maxProduct(TreeNode* root) {

const int kMod = 1e9 + 7;

long s = 0;

long ans = 0;

function<int(TreeNode*)> sum = [&](TreeNode* r) {

if (!r) return 0;

int sl = sum(r->left);

int sr = sum(r->right);

if (s) ans = max({ans, (s - sl) * sl, (s - sr) * sr});

return r->val + sl + sr;

};

s = sum(root);

sum(root);

return ans % kMod;

}

};

花花酱 LeetCode 1302. Deepest Leaves Sum

By zxi on January 31, 2020

Given a binary tree, return the sum of values of its deepest leaves.

Example 1:

Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

Constraints:

The number of nodes in the tree is between 1 and 10^4.
The value of nodes is between 1 and 100.

Solution 1: Recursion

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int deepestLeavesSum(TreeNode* root) {

int sum = 0;

int max_depth = 0;

function<void(TreeNode*, int)> dfs = [&](TreeNode* n, int d) {

if (!n) return;

if (d > max_depth) {

max_depth = d;

sum = 0;

}

if (d == max_depth) sum += n->val;

dfs(n->left, d + 1);

dfs(n->right, d + 1);

};

dfs(root, 0);

return sum;

}

};