Problem:
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 4.
Idea:
Dynamic programming
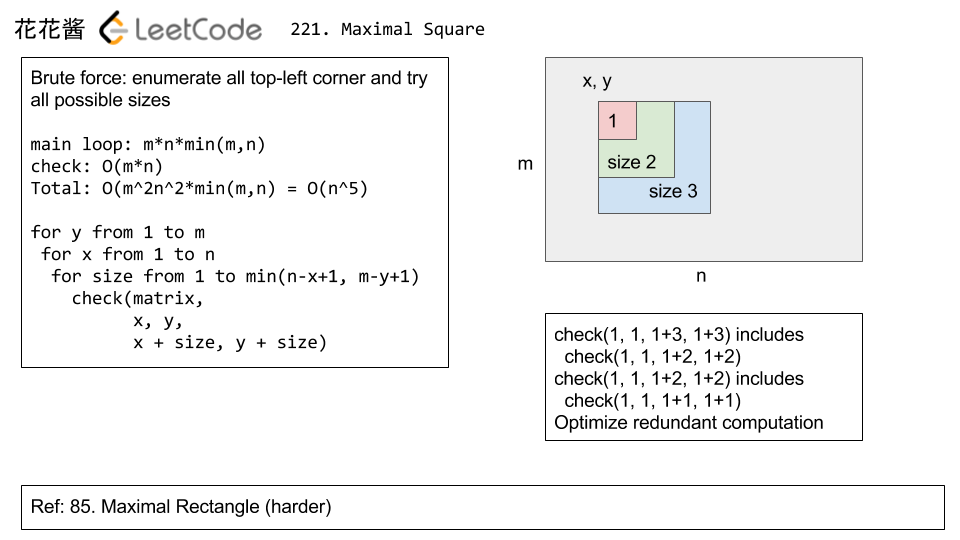
Solution 0: O(n^5)
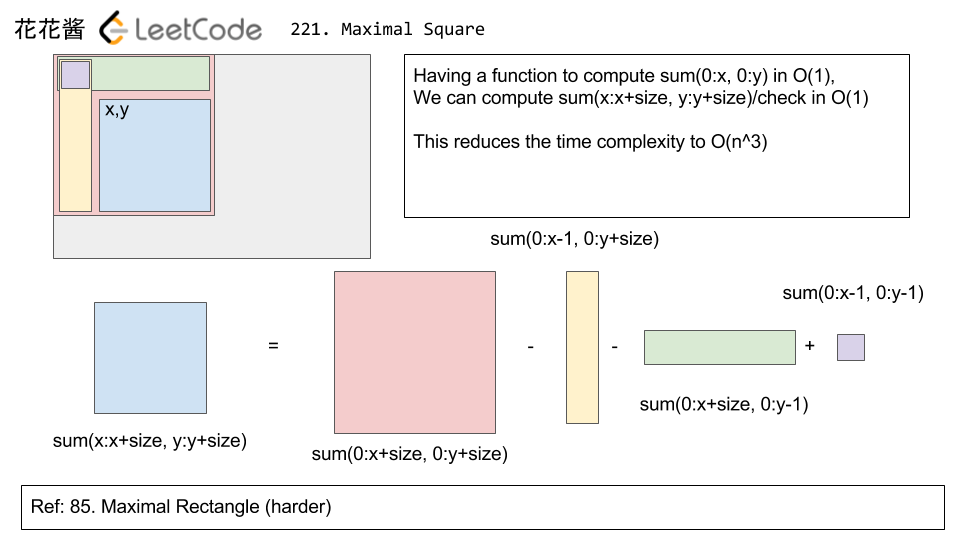
Solution 1: O(n^3)
Solution 2: O(n^2)
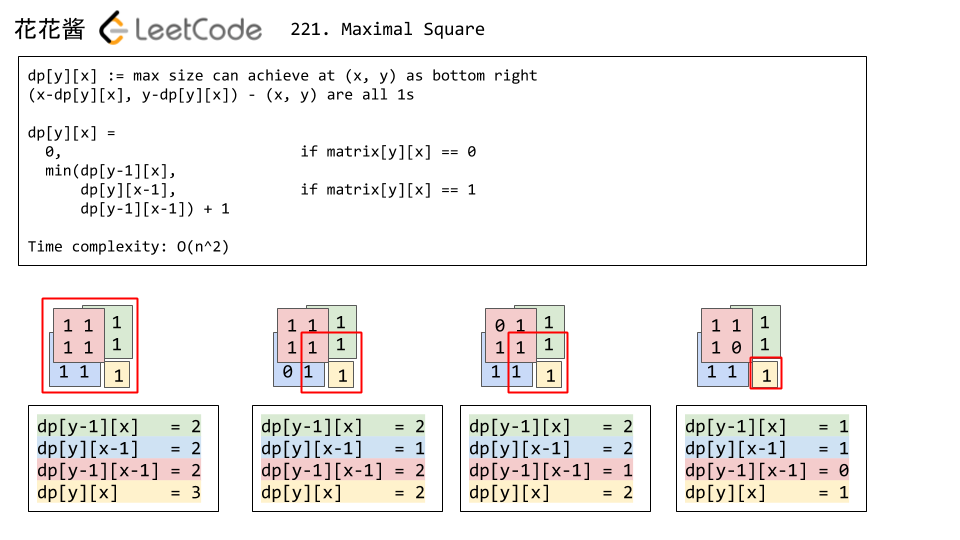
Solution 1:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
// Author: Huahua // Time complexity: O(n^3) // Running time: 39 ms class Solution { public: int maximalSquare(vector<vector<char>>& matrix) { if (matrix.empty()) return 0; int m = matrix.size(); int n = matrix[0].size(); // sums[i][j] = sum(matrix[0][0] ~ matrix[i-1][j-1]) vector<vector<int>> sums(m + 1, vector<int>(n + 1, 0)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) sums[i][j] = matrix[i - 1][j - 1] - '0' + sums[i - 1][j] + sums[i][j - 1] - sums[i - 1][j - 1]; int ans = 0; for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) for (int k = min(m - i + 1, n - j + 1); k > 0; --k) { int sum = sums[i + k - 1][j + k - 1] - sums[i + k - 1][j - 1] - sums[i - 1][j + k - 1] + sums[i - 1][j - 1]; // full of 1 if (sum == k*k) { ans = max(ans, sum); break; } } return ans; } }; |
Solution 2:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
// Author: Huahua // Time complexity: O(n^2) // Running time: 6 ms class Solution { public: int maximalSquare(vector<vector<char>>& matrix) { if (matrix.empty()) return 0; int m = matrix.size(); int n = matrix[0].size(); vector<vector<int>> sizes(m, vector<int>(n, 0)); int ans = 0; for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) { sizes[i][j] = matrix[i][j] - '0'; if (!sizes[i][j]) continue; if (i == 0 || j == 0) { // do nothing } else if (i == 0) sizes[i][j] = sizes[i][j - 1] + 1; else if (j == 0) sizes[i][j] = sizes[i - 1][j] + 1; else sizes[i][j] = min(min(sizes[i - 1][j - 1], sizes[i - 1][j]), sizes[i][j - 1]) + 1; ans = max(ans, sizes[i][j]*sizes[i][j]); } return ans; } }; |
请尊重作者的劳动成果，转载请注明出处！花花保留对文章／视频的所有权利。
如果您喜欢这篇文章／视频，欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.
Paypal
Venmo
huahualeetcode
huahualeetcode
微信打赏
Be First to Comment