A k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal. The integers in the magic square do not have to be distinct. Every 1 x 1 grid is trivially a magic square.
Given an m x n integer grid, return the size (i.e., the side length k) of the largest magic square that can be found within this grid.
Example 1:
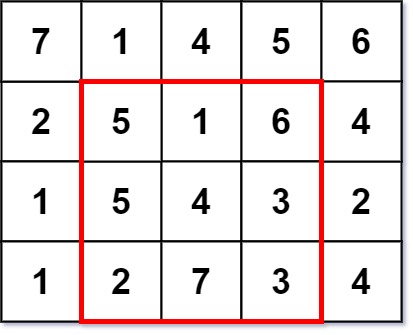
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]] Output: 3 Explanation: The largest magic square has a size of 3. Every row sum, column sum, and diagonal sum of this magic square is equal to 12. - Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12 - Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12 - Diagonal sums: 5+4+3 = 6+4+2 = 12
Example 2:
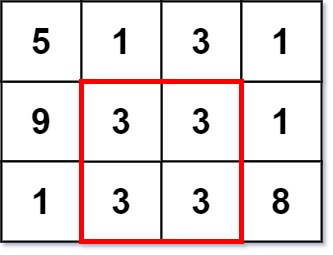
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]] Output: 2
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 106
Solution: Brute Force w/ Prefix Sum
Compute the prefix sum for each row and each column.
And check all possible squares.
Time complexity: O(m*n*min(m,n)2)
Space complexity: O(m*n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
// Author: Huahua class Solution { public: int largestMagicSquare(vector<vector<int>>& grid) { const int m = grid.size(); const int n = grid[0].size(); vector<vector<int>> rows(m, vector<int>(n + 1)); vector<vector<int>> cols(n, vector<int>(m + 1)); for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) { rows[i][j + 1] = rows[i][j] + grid[i][j]; cols[j][i + 1] = cols[j][i] + grid[i][j]; } for (int k = min(m, n); k >= 2; --k) for (int i = 0; i + k <= m; ++i) for (int j = 0; j + k <= n; ++j) { vector<int> s; for (int r = 0; r < k; ++r) s.push_back(rows[i + r][j + k] - rows[i + r][j]); for (int c = 0; c < k; ++c) s.push_back(cols[j + c][i + k] - cols[j + c][i]); int d1 = 0; int d2 = 0; for (int d = 0; d < k; ++d) { d1 += grid[i + d][j + d]; d2 += grid[i + d][j + k - d - 1]; } s.push_back(d1); s.push_back(d2); if (count(begin(s), end(s), s[0]) == s.size()) return k; } return 1; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment