Given a weighted undirected connected graph with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between nodes fromi and toi. A minimum spanning tree (MST) is a subset of the edges of the graph that connects all vertices without cycles and with the minimum possible total edge weight.
Find all the critical and pseudo-critical edges in the minimum spanning tree (MST) of the given graph. An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. A pseudo-critical edge, on the other hand, is that which can appear in some MSTs but not all.
Note that you can return the indices of the edges in any order.
Example 1:
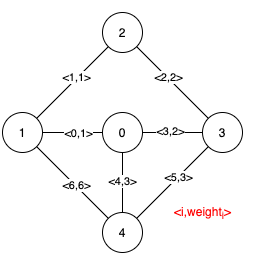
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]] Output: [[0,1],[2,3,4,5]] Explanation: The figure above describes the graph. The following figure shows all the possible MSTs: Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output. The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.
Example 2:
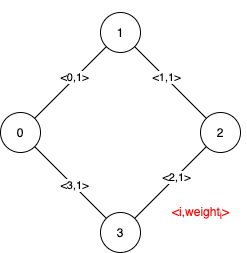
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]] Output: [[],[0,1,2,3]] Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.
Constraints:
2 <= n <= 1001 <= edges.length <= min(200, n * (n - 1) / 2)edges[i].length == 30 <= fromi < toi < n1 <= weighti <= 1000- All pairs
(fromi, toi)are distinct.
Solution: Brute Force?

For each edge
1. exclude it and build a MST, cost increased => critical
2. for a non critical edge, force include it and build a MST, cost remains the same => pseudo critical
Proof of 2, if a non critical / non pseudo critical edge was added into the MST, the total cost must be increased. So if the cost remains the same, must be the other case. Since we know the edge is non-critical, so it has to be pseudo critical.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
// Author: Huahua class UnionFind { public: explicit UnionFind(int n): p_(n), r_(n) { iota(begin(p_), end(p_), 0); } // e.g. p[i] = i int Find(int x) { return p_[x] == x ? x : p_[x] = Find(p_[x]); } bool Union(int x, int y) { int rx = Find(x); int ry = Find(y); if (rx == ry) return false; if (r_[rx] == r_[ry]) { p_[rx] = ry; ++r_[ry]; } else if (r_[rx] > r_[ry]) { p_[ry] = rx; } else { p_[rx] = ry; } return true; } private: vector<int> p_, r_; }; class Solution { public: vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) { // Record the original id. for (int i = 0; i < edges.size(); ++i) edges[i].push_back(i); // Sort edges by weight. sort(begin(edges), end(edges), [&](const auto& e1, const auto& e2){ if (e1[2] != e2[2]) return e1[2] < e2[2]; return e1 < e2; }); // Cost of MST, ex: edge to exclude, in: edge to include. auto MST = [&](int ex = -1, int in = -1) -> int { UnionFind uf(n); int cost = 0; int count = 0; if (in >= 0) { cost += edges[in][2]; uf.Union(edges[in][0], edges[in][1]); count++; } for (int i = 0; i < edges.size(); ++i) { if (i == ex) continue; if (!uf.Union(edges[i][0], edges[i][1])) continue; cost += edges[i][2]; ++count; } return count == n - 1 ? cost : INT_MAX; }; const int min_cost = MST(); vector<int> criticals; vector<int> pseudos; for (int i = 0; i < edges.size(); ++i) { // Cost increased or can't form a tree. if (MST(i) > min_cost) { criticals.push_back(edges[i][3]); } else if (MST(-1, i) == min_cost) { pseudos.push_back(edges[i][3]); } } return {criticals, pseudos}; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment