Given a 2D grid consisting of 1s (land) and 0s (water). An island is a maximal 4-directionally (horizontal or vertical) connected group of 1s.
The grid is said to be connected if we have exactly one island, otherwise is said disconnected.
In one day, we are allowed to change any single land cell (1) into a water cell (0).
Return the minimum number of days to disconnect the grid.
Example 1:
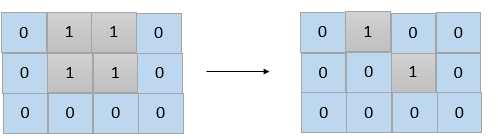
Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]] Output: 2 Explanation: We need at least 2 days to get a disconnected grid. Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.
Example 2:
Input: grid = [[1,1]] Output: 2 Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.
Example 3:
Input: grid = [[1,0,1,0]] Output: 0
Example 4:
Input: grid = [[1,1,0,1,1], [1,1,1,1,1], [1,1,0,1,1], [1,1,0,1,1]] Output: 1
Example 5:
Input: grid = [[1,1,0,1,1], [1,1,1,1,1], [1,1,0,1,1], [1,1,1,1,1]] Output: 2
Constraints:
1 <= grid.length, grid[i].length <= 30grid[i][j]is0or1.
Solution: Brute Force
We need at most two days to disconnect an island.
1. check if we have more than one islands. (0 days)
2. For each 1 cell, change it to 0 and check how many islands do we have. (1 days)
3. Otherwise, 2 days
Time complexity: O(m^2*n^2)
Space complexity: O(m*n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
class Solution { public: int minDays(vector<vector<int>>& grid) { const int n = grid.size(); const int m = grid[0].size(); const vector<int> dirs{0, 1, 0, -1, 0}; vector<int> seen(n * m); function<void(int, int)> dfs = [&](int x, int y) { if (x < 0 || y < 0 || x >= m || y >= n) return; if (grid[y][x] == 0) return; if (seen[y * m + x]++) return; for (int i = 0; i < 4; ++i) dfs(x + dirs[i], y + dirs[i + 1]); }; function<bool()> disconnected = [&]() { int count = 0; fill(begin(seen), end(seen), 0); for (int y = 0; y < n; ++y) for (int x = 0; x < m; ++x) if (grid[y][x] && !seen[y * m + x]) { dfs(x, y); if (++count > 1) return true; } return false; }; if (disconnected()) return 0; for (int y = 0; y < n; ++y) for (int x = 0; x < m; ++x) { if (!grid[y][x]) continue; grid[y][x] = 0; if (disconnected()) return 1; grid[y][x] = 1; } return 2; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment