There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.
You are given a string colors where colors[i] is a lowercase English letter representing the color of the ith node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [aj, bj] indicates that there is a directed edge from node aj to node bj.
A valid path in the graph is a sequence of nodes x1 -> x2 -> x3 -> ... -> xk such that there is a directed edge from xi to xi+1 for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.
Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.
Example 1:
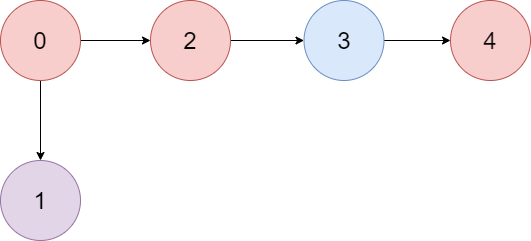
Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3
Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).
Example 2:
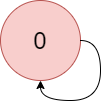
Input: colors = "a", edges = [[0,0]] Output: -1 Explanation: There is a cycle from 0 to 0.
Constraints:
n == colors.lengthm == edges.length1 <= n <= 1050 <= m <= 105colorsconsists of lowercase English letters.0 <= aj, bj < n
Solution: Topological Sorting
freq[n][c] := max freq of color c after visiting node n.
Time complexity: O(n)
Space complexity: O(n*26)
python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class Solution: def largestPathValue(self, colors: str, edges: List[List[int]]) -> int: INF = 1e9 n = len(colors) g = [[] for _ in range(n)] for u, v in edges: g[u].append(v) visited = [0] * n freq = [[0] * 26 for _ in range(n)] def dfs(u: int) -> int: idx = ord(colors[u]) - ord('a') if not visited[u]: visited[u] = 1 # visiting for v in g[u]: if (dfs(v) == INF): return INF for c in range(26): freq[u][c] = max(freq[u][c], freq[v][c]) freq[u][idx] += 1 visited[u] = 2 # done return freq[u][idx] if visited[u] == 2 else INF ans = 0 for u in range(n): ans = max(ans, dfs(u)) if ans == INF: break return -1 if ans == INF else ans |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment