Problem
Given a set of N people (numbered 1, 2, ..., N), we would like to split everyone into two groups of any size.
Each person may dislike some other people, and they should not go into the same group.
Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.
Return true if and only if it is possible to split everyone into two groups in this way.
Example 1:
Input: N = 4, dislikes = [[1,2],[1,3],[2,4]] Output: true Explanation: group1 [1,4], group2 [2,3]
Example 2:
Input: N = 3, dislikes = [[1,2],[1,3],[2,3]] Output: false
Example 3:
Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]] Output: false
Note:
1 <= N <= 20000 <= dislikes.length <= 100001 <= dislikes[i][j] <= Ndislikes[i][0] < dislikes[i][1]- There does not exist
i != jfor whichdislikes[i] == dislikes[j].
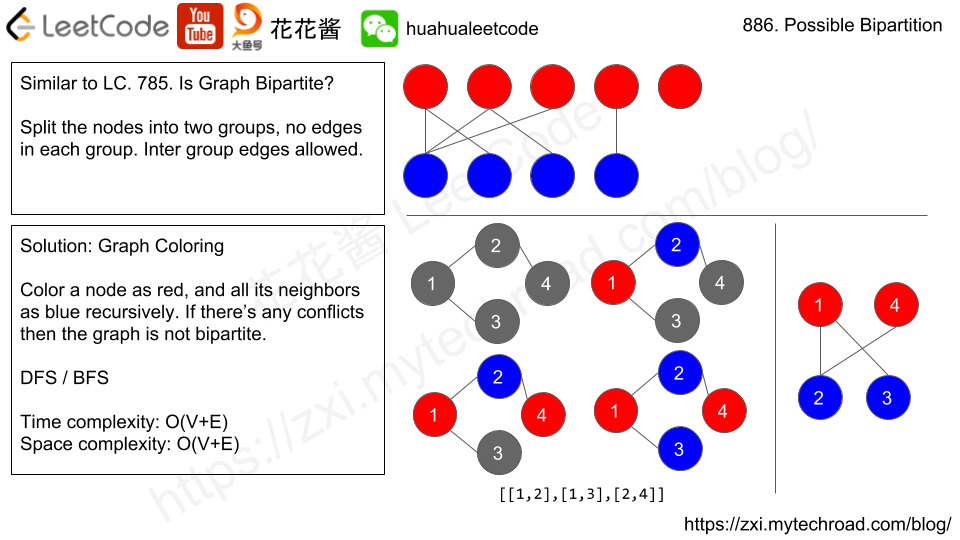
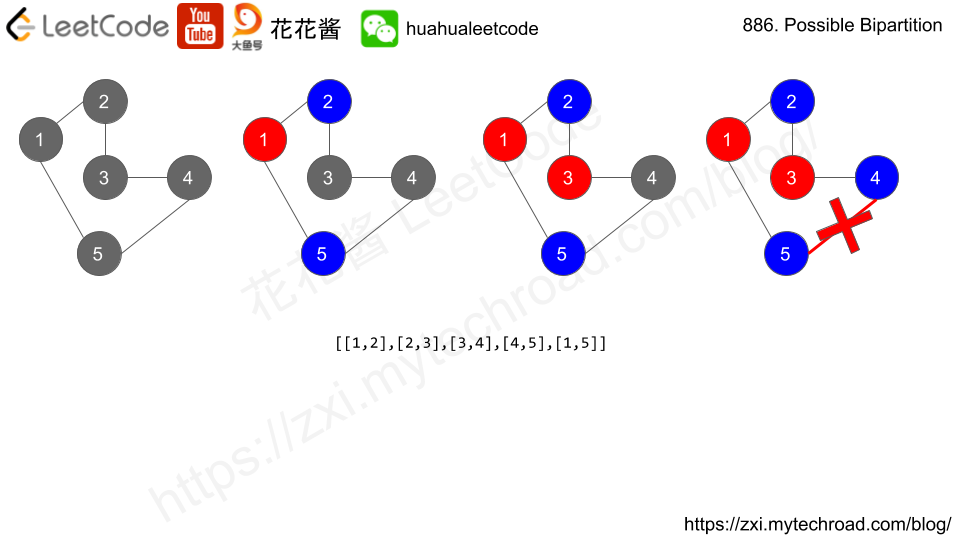
Solution: Graph Coloring
Color a node with one color, and color all it’s disliked nodes with another color, if can not finish return false.
Time complexity: O(V+E)
Space complexity: O(V+E)
C++ / DFS
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
// Author: Huahua // Running time: 96 ms class Solution { public: bool possibleBipartition(int N, vector<vector<int>>& dislikes) { g_ = vector<vector<int>>(N); for (const auto& d : dislikes) { g_[d[0] - 1].push_back(d[1] - 1); g_[d[1] - 1].push_back(d[0] - 1); } colors_ = vector<int>(N, 0); // 0: unknown, 1: red, -1: blue for (int i = 0; i < N; ++i) if (colors_[i] == 0 && !dfs(i, 1)) return false; return true; } private: vector<vector<int>> g_; vector<int> colors_; bool dfs(int cur, int color) { colors_[cur] = color; for (int nxt : g_[cur]) { if (colors_[nxt] == color) return false; if (colors_[nxt] == 0 && !dfs(nxt, -color)) return false; } return true; } }; |
C++ / BFS
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// Author: Huahua // Running time: 100 ms class Solution { public: bool possibleBipartition(int N, vector<vector<int>>& dislikes) { vector<vector<int>> g(N); for (const auto& d : dislikes) { g[d[0] - 1].push_back(d[1] - 1); g[d[1] - 1].push_back(d[0] - 1); } queue<int> q; vector<int> colors(N, 0); // 0: unknown, 1: red, -1: blue for (int i = 0; i < N; ++i) { if (colors[i] != 0) continue; q.push(i); colors[i] = 1; while (!q.empty()) { int cur = q.front(); q.pop(); for (int nxt : g[cur]) { if (colors[nxt] == colors[cur]) return false; if (colors[nxt] != 0) continue; colors[nxt] = -colors[cur]; q.push(nxt); } } } return true; } }; |
Related Problem
请尊重作者的劳动成果，转载请注明出处！花花保留对文章／视频的所有权利。
如果您喜欢这篇文章／视频，欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.
Paypal
Venmo
huahualeetcode
huahualeetcode
微信打赏
Be First to Comment