Problem
Given a non-empty array of unique positive integers A, consider the following graph:
- There are
A.lengthnodes, labelledA[0]toA[A.length - 1]; - There is an edge between
A[i]andA[j]if and only ifA[i]andA[j]share a common factor greater than 1.
Return the size of the largest connected component in the graph.
Example 1:
Input: [4,6,15,35] Output: 4
Example 2:
Input: [20,50,9,63] Output: 2
Example 3:
Input: [2,3,6,7,4,12,21,39] Output: 8
Note:
1 <= A.length <= 200001 <= A[i] <= 100000
Solution: Union Find
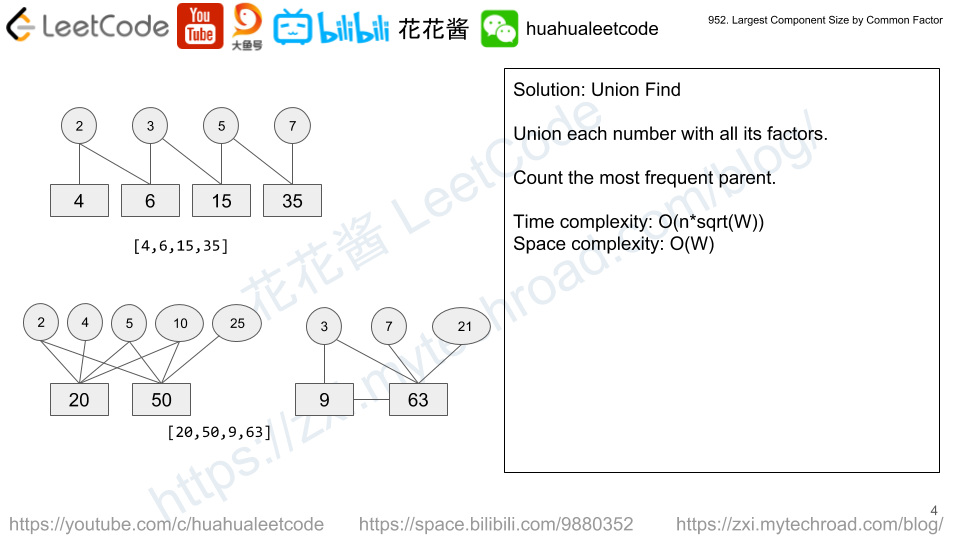
For each number, union itself with all its factors.
E.g. 6, union(6,2), union(6,3)
Time complexity: \( O(\Sigma{sqrt(A[i])}) \)
Space complexity: \( O(max(A)) \)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
// Author: Huahua, running time: 148 ms class DSU { public: DSU(int n): p_(n) { for (int i = 0; i < n; ++i) p_[i] = i; } void Union(int x, int y) { p_[Find(x)] = p_[Find(y)]; } int Find(int x) { if (p_[x] != x) p_[x] = Find(p_[x]); return p_[x]; } private: vector<int> p_; }; class Solution { public: int largestComponentSize(vector<int>& A) { int n = *max_element(begin(A), end(A)); DSU dsu(n + 1); for (int a : A) { int t = sqrt(a); for (int k = 2; k <= t; ++k) if (a % k == 0) { dsu.Union(a, k); dsu.Union(a, a / k); } } unordered_map<int, int> c; int ans = 1; for (int a : A) ans = max(ans, ++c[dsu.Find(a)]); return ans; } }; |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# Author: Huahua, running time: 3432 ms class Solution: def largestComponentSize(self, A): p = list(range(max(A) + 1)) def find(x): while p[x] != x: p[x] = p[p[x]] x = p[x] return x def union(x, y): p[find(x)] = p[find(y)] for a in A: for k in range(2, int(math.sqrt(a) + 1)): if a % k == 0: union(a, k) union(a, a // k) return collections.Counter([find(a) for a in A]).most_common(1)[0][1] |
请尊重作者的劳动成果，转载请注明出处！花花保留对文章／视频的所有权利。
如果您喜欢这篇文章／视频，欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.
Paypal
Venmo
huahualeetcode
huahualeetcode
微信打赏
Be First to Comment