花花酱 LeetCode 1326. Minimum Number of Taps to Open to Water a Garden

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:

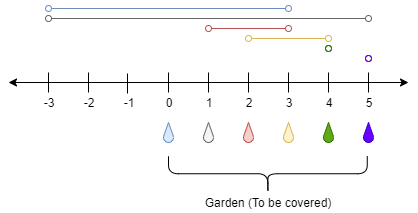
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Example 3:

Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
Output: 3

Example 4:

Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
Output: 2

Example 5:

Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
Output: 1

Constraints:

• 1 <= n <= 10^4
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

Solution 1: Greedy

Reduce to 1024. Video Stitching

Time complexity: O(nlogn)
Space complexity: O(n)

Solution 2: Greedy

Reduce to 45. Jump Game II

Time complexity: O(n)
Space complexity: O(n)