Given a string num representing the digits of a very large integer and an integer k.
You are allowed to swap any two adjacent digits of the integer at most k times.
Return the minimum integer you can obtain also as a string.
Example 1:
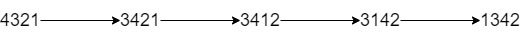
Input: num = "4321", k = 4 Output: "1342" Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.
Example 2:
Input: num = "100", k = 1 Output: "010" Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.
Example 3:
Input: num = "36789", k = 1000 Output: "36789" Explanation: We can keep the number without any swaps.
Example 4:
Input: num = "22", k = 22 Output: "22"
Example 5:
Input: num = "9438957234785635408", k = 23 Output: "0345989723478563548"
Constraints:
1 <= num.length <= 30000numcontains digits only and doesn’t have leading zeros.1 <= k <= 10^9
Solution: Greedy + Recursion (Update: TLE after 7/6/2020)
Move the smallest number to the left and recursion on the right substring with length equals to n -= 1.
4321 k = 4 => 1 + solve(432, 4-3) = 1 + solve(432, 1) = 1 + 3 + solve(42, 0) = 1 + 3 + 42 = 1342.
Time complexity: O(n^2)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
// Author: Huahua class Solution { public: string minInteger(string num, int k) { const int n = num.size(); if (k >= n * (n - 1) / 2) { sort(begin(num), end(num)); return num; } int s = 0; while (k > 0 && s < n) { auto bit = begin(num); auto it = min_element(bit + s, bit + min(s + k + 1, n)); k -= distance(bit + s, it); rotate(bit + (s++), it, next(it)); } return num; } }; |
Solution 2: Binary Indexed Tree / Fenwick Tree


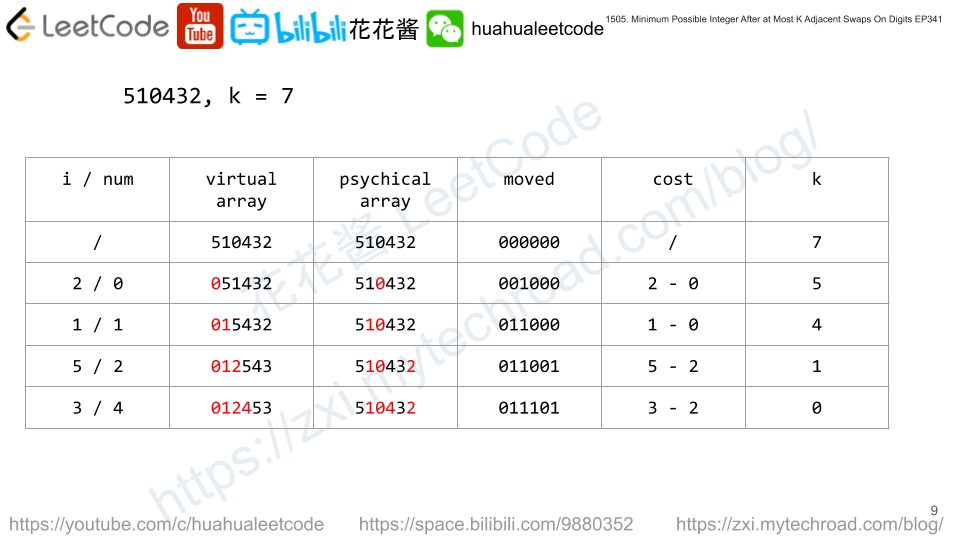
Moving elements in a string is a very expensive operation, basically O(n) per op. Actually, we don’t need to move the elements physically, instead we track how many elements before i has been moved to the “front”. Thus we know the cost to move the i-th element to the “front”, which is i – elements_moved_before_i or prefix_sum(0~i-1) if we mark moved element as 1.
We know BIT / Fenwick Tree is good for dynamic prefix sum computation which helps to reduce the time complexity to O(nlogn).
Time complexity: O(nlogn)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
// Author: Huahua class Fenwick { public: explicit Fenwick(int n) : sums_(n + 1) {} void update(int i, int delta) { ++i; while (i < sums_.size()) { sums_[i] += delta; i += i & -i; } } int query(int i) { ++i; int ans = 0; while (i > 0) { ans += sums_[i]; i -= i & -i; } return ans; } private: vector<int> sums_; }; class Solution { public: string minInteger(string num, int k) { const int n = num.length(); vector<queue<int>> pos(10); for (int i = 0; i < n; ++i) pos[num[i] - '0'].push(i); Fenwick tree(n); vector<int> used(n); string ans; while (k > 0 & ans.length() < n) { for (int d = 0; d < 10; ++d) { if (pos[d].empty()) continue; const int i = pos[d].front(); const int cost = i - tree.query(i - 1); if (cost > k) continue; k -= cost; ans += ('0' + d); tree.update(i, 1); used[i] = true; pos[d].pop(); break; } }; for (int i = 0; i < n; ++i) if (!used[i]) ans += num[i]; return ans; } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
// Author: Huahua class Solution { class Fenwick { private int[] sums; public Fenwick(int n) { this.sums = new int[n + 1]; } public void update(int i, int delta) { ++i; while (i < sums.length) { this.sums[i] += delta; i += i & -i; } } public int query(int i) { int ans = 0; ++i; while (i > 0) { ans += this.sums[i]; i -= i & -i; } return ans; } } public String minInteger(String num, int k) { int n = num.length(); var used = new boolean[n]; var pos = new ArrayList<ArrayDeque<Integer>>(); for (int i = 0; i <= 9; ++i) pos.add(new ArrayDeque<Integer>()); for (int i = 0; i < num.length(); ++i) pos.get(num.charAt(i) - '0').offer(i); var tree = new Fenwick(n); var sb = new StringBuilder(); while (k > 0 && sb.length() < n) { for (int d = 0; d <= 9; ++d) { Integer i = pos.get(d).peek(); if (i == null) continue; int cost = i - tree.query(i - 1); if (cost > k) continue; sb.append((char)(d + '0')); k -= cost; pos.get(d).removeFirst(); tree.update(i, 1); used[i] = true; break; } } for (int i = 0; i < n; ++i) if (!used[i]) sb.append(num.charAt(i)); return sb.toString(); } } |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# Author: Huahua class Fenwick: def __init__(self, n): self.sums = [0] * (n + 1) def query(self, i): ans = 0 i += 1 while i > 0: ans += self.sums[i]; i -= i & -i return ans def update(self, i, delta): i += 1 while i < len(self.sums): self.sums[i] += delta i += i & -i class Solution: def minInteger(self, num: str, k: int) -> str: n = len(num) used = [False] * n pos = [deque() for _ in range(10)] for i, c in enumerate(num): pos[ord(c) - ord("0")].append(i) tree = Fenwick(n) ans = [] while k > 0 and len(ans) < n: for d in range(10): if not pos[d]: continue i = pos[d][0] cost = i - tree.query(i - 1) if cost > k: continue k -= cost ans.append(chr(d + ord("0"))) tree.update(i, 1) used[i] = True pos[d].popleft() break for i in range(n): if not used[i]: ans.append(num[i]) return "".join(ans) |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment