Huahua’s Tech Road

花花酱 LeetCode 1697. Checking Existence of Edge Length Limited Paths

By zxi on December 20, 2020

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [u_i, v_i, dis_i] denotes an edge between nodes u_i and v_i with distance dis_i. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [p_j, q_j, limit_j], your task is to determine for each queries[j] whether there is a path between p_j and q_jsuch that each edge on the path has a distance strictly less than limit_j .

Return a boolean array answer, where answer.length == queries.length and the j^th value of answer is true if there is a path for queries[j] is true, and false otherwise.

Example 1:

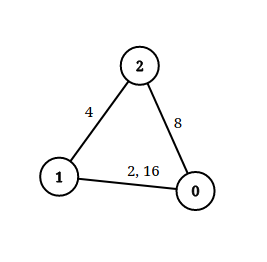
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

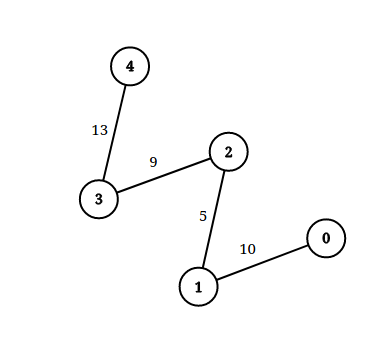
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.

Constraints:

2 <= n <= 10⁵
1 <= edgeList.length, queries.length <= 10⁵
edgeList[i].length == 3
queries[j].length == 3
0 <= u_i, v_i, p_j, q_j <= n - 1
u_i != v_i
p_j != q_j
1 <= dis_i, limit_j <= 10⁹
There may be multiple edges between two nodes.

Solution: Union Find

Since queries are offline, we can reorder them to optimize time complexity. Answer queries by their limits in ascending order while union edges by weights up to the limit. In this case, we just need to go through the entire edge list at most once.

Time complexity: O(QlogQ + ElogE)
Space complexity: O(Q + E)

C++

// Author: Huahua

class Solution {

public:

vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& E, vector<vector<int>>& Q) {

vector<int> parents(n);

iota(begin(parents), end(parents), 0);

function<int(int)> find = [&](int x) {

return parents[x] == x ? x : parents[x] = find(parents[x]);

};

const int m = Q.size();

for (int i = 0; i < m; ++i) Q[i].push_back(i);

// Sort edges by weight in ascending order.

sort(begin(E), end(E), [](const auto& a, const auto& b) { return a[2] < b[2]; });

// Sort queries by limit in ascending order

sort(begin(Q), end(Q), [](const auto& a, const auto& b) { return a[2] < b[2]; });

vector<bool> ans(m);

int i = 0;

for (const auto& q : Q) {

while (i < E.size() && E[i][2] < q[2])

parents[find(E[i++][0])] = find(E[i][1]);

ans[q[3]] = find(q[0]) == find(q[1]);

}

return ans;

}

};

花花酱 LeetCode 1696. Jump Game VI

By zxi on December 20, 2020

You are given a 0-indexed integer array nums and an integer k.

You are initially standing at index 0. In one move, you can jump at most k steps forward without going outside the boundaries of the array. That is, you can jump from index i to any index in the range [i + 1, min(n - 1, i + k)] inclusive.

You want to reach the last index of the array (index n - 1). Your score is the sum of all nums[j] for each index j you visited in the array.

Return the maximum score you can get.

Example 1:

Input: nums = [1,-1,-2,4,-7,3], k = 2
Output: 7
Explanation: You can choose your jumps forming the subsequence [1,-1,4,3] (underlined above). The sum is 7.

Example 2:

Input: nums = [10,-5,-2,4,0,3], k = 3
Output: 17
Explanation: You can choose your jumps forming the subsequence [10,4,3] (underlined above). The sum is 17.

Example 3:

Input: nums = [1,-5,-20,4,-1,3,-6,-3], k = 2
Output: 0

Constraints:

1 <= nums.length, k <= 10⁵
-10⁴ <= nums[i] <= 10⁴

Solution: DP + Monotonic Queue

dp[i] = nums[i] + max(dp[j]) i – k <= j < i

Brute force time complexity: O(n*k) => TLE

Python3 / TLE

# Author: Huahua 52/58 Passed (TLE)

class Solution:

def maxResult(self, nums: List[int], k: int) -> int:

@lru_cache(None)

def dp(i: int) -> int:

return nums[0] if i == 0 else nums[i] + max(dp(j) for j in range(max(0, i - k), i))

return dp(len(nums) - 1)

This problem can be reduced to find the maximum for a sliding window that can be solved by monotonic queue.

Time complexity: O(n)
Space complexity: O(n+k) -> O(k)

C++

// Author: Huahua

class Solution {

public:

int maxResult(vector<int>& nums, int k) {

const int n = nums.size();

vector<int> dp(n);

deque<int> q{{0}};

dp[0] = nums[0];

for (int i = 1; i < n; ++i) {

dp[i] = nums[i] + dp[q.front()];

while (!q.empty() && dp[i] >= dp[q.back()]) q.pop_back();

while (!q.empty() && i - q.front() >= k) q.pop_front();

q.push_back(i);

}

return dp[n - 1];

}

};

C++/O(n) Space

// Author: Huahua

class Solution {

public:

int maxResult(vector<int>& nums, int k) {

const int n = nums.size();

deque<pair<int, int>> q{{nums[0], 0}};

for (int i = 1; i < n; ++i) {

const int cur = nums[i] + q.front().first;

while (!q.empty() && cur >= q.back().first)

q.pop_back();

while (!q.empty() && i - q.front().second >= k)

q.pop_front();

q.emplace_back(cur, i);

}

for (const auto& [v, i] : q)

if (i == n - 1) return v;

return 0;

}

};

花花酱 LeetCode 1695. Maximum Erasure Value

By zxi on December 20, 2020

You are given an array of positive integers nums and want to erase a subarray containing unique elements. The score you get by erasing the subarray is equal to the sum of its elements.

Return the maximum score you can get by erasing exactly one subarray.

An array b is called to be a subarray of a if it forms a contiguous subsequence of a, that is, if it is equal to a[l],a[l+1],...,a[r] for some (l,r).

Example 1:

Input: nums = [4,2,4,5,6]
Output: 17
Explanation: The optimal subarray here is [2,4,5,6].

Example 2:

Input: nums = [5,2,1,2,5,2,1,2,5]
Output: 8
Explanation: The optimal subarray here is [5,2,1] or [1,2,5].

Constraints:

1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁴

Solution: Sliding window + Hashset

Maintain a window that has no duplicate elements.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maximumUniqueSubarray(vector<int>& nums) {

const int n = nums.size();

unordered_set<int> t;

int ans = 0;

for (int l = 0, r = 0, s = 0; r < n; ++r) {

while (t.count(nums[r]) && l < r) {

s -= nums[l];

t.erase(nums[l++]);

}

t.insert(nums[r]);

ans = max(ans, s += nums[r]);

}

return ans;

}

};

花花酱 LeetCode 1694. Reformat Phone Number

By zxi on December 20, 2020

You are given a phone number as a string number. number consists of digits, spaces ' ', and/or dashes '-'.

You would like to reformat the phone number in a certain manner. Firstly, remove all spaces and dashes. Then, group the digits from left to right into blocks of length 3 until there are 4 or fewer digits. The final digits are then grouped as follows:

2 digits: A single block of length 2.
3 digits: A single block of length 3.
4 digits: Two blocks of length 2 each.

The blocks are then joined by dashes. Notice that the reformatting process should never produce any blocks of length 1 and produce at most two blocks of length 2.

Return the phone number after formatting.

Example 1:

Input: number = "1-23-45 6"
Output: "123-456"
Explanation: The digits are "123456".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123".
Step 2: There are 3 digits remaining, so put them in a single block of length 3. The 2nd block is "456".
Joining the blocks gives "123-456".

Example 2:

Input: number = "123 4-567"
Output: "123-45-67"
Explanation: The digits are "1234567".
Step 1: There are more than 4 digits, so group the next 3 digits. The 1st block is "123".
Step 2: There are 4 digits left, so split them into two blocks of length 2. The blocks are "45" and "67".
Joining the blocks gives "123-45-67".

Example 3:

Input: number = "123 4-5678"
Output: "123-456-78"
Explanation: The digits are "12345678".
Step 1: The 1st block is "123".
Step 2: The 2nd block is "456".
Step 3: There are 2 digits left, so put them in a single block of length 2. The 3rd block is "78".
Joining the blocks gives "123-456-78".

Example 4:

Input: number = "12"
Output: "12"

Example 5:

Input: number = "--17-5 229 35-39475 "
Output: "175-229-353-94-75"

Constraints:

2 <= number.length <= 100
number consists of digits and the characters '-' and ' '.
There are at least two digits in number.

Solution:

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

string reformatNumber(string number) {

string ans;

const int total = count_if(begin(number), end(number),

[](char c) { return isdigit(c); });

int l = 0;

for (char c : number) {

if (!isdigit(c)) continue;

ans += c;

++l;

if ((l % 3 == 0 && total - l >= 4) ||

(total % 3 != 0 && total - l == 2)

|| (total % 3 == 0 && total - l == 3))

ans += "-";

}

return ans;

}

};

花花酱 LeetCode 1691. Maximum Height by Stacking Cuboids

By zxi on December 13, 2020

Given n cuboids where the dimensions of the i^th cuboid is cuboids[i] = [width_i, length_i, height_i] (0-indexed). Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if width_i <= width_j and length_i <= length_j and height_i <= height_j. You can rearrange any cuboid’s dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

Example 1:

Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
Output: 190
Explanation:
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
The total height is 95 + 50 + 45 = 190.

Example 2:

Input: cuboids = [[38,25,45],[76,35,3]]
Output: 76
Explanation:
You can't place any of the cuboids on the other.
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.

Example 3:

Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
Output: 102
Explanation:
After rearranging the cuboids, you can see that all cuboids have the same dimension.
You can place the 11x7 side down on all cuboids so their heights are 17.
The maximum height of stacked cuboids is 6 * 17 = 102.

Constraints:

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

Solution: Math/Greedy + DP

Direct DP is very hard, since there is no orders.

We have to find some way to sort the cuboids such that cuboid i can NOT stack on cuboid j if i > j. Then dp[i] = max(dp[j]) + height[i], 0 <= j < i, for each i, find the best base j and stack on top of it.
ans = max(dp)

We can sort the cuboids by their sorted dimensions, and cuboid i can stack stack onto cuboid j if and only if w[i] <= w[j] and l[i] <= l[j] and h[i] <= h[j].

First of all, we need to prove that all heights must come from the largest dimension of each cuboid.

1. If the top of the stack is A1*A2*A3, A3 < max(A1, A2), we can easily swap A3 with max(A1, A2), it’s still stackable but we get larger heights.
e.g. 3x5x4, base is 3×5, height is 4, we can rotate to get base of 3×4 with height of 5.

2. If a middle cuboid A of size A1*A2*A3, assuming A1 >= A2, A1 > A3, on top of A we have another cuboid B of size B1*B2*B3, B1 <= B2 <= B3.
We have A1 >= B1, A2 >= B2, A3 >= B3, by rotating A we have A3*A2*A1
A3 >= B3 >= B1, A2 >= B2, A1 > A3 >= B3, so B can be still on top of A, and we get larger height.

e.g. A: 3x5x4, B: 2x3x4
A -> 3x4x5, B is still stackable.

…

Time complexity: O(n^2)
Space complexity: O(n^2)

C++

// Author: Huahua

class Solution {

public:

int maxHeight(vector<vector<int>>& A) {

A.push_back({0, 0, 0});

const int n = A.size();

for (auto& box : A) sort(begin(box), end(box));

sort(begin(A), end(A));

vector<int> dp(n);

for (int i = 0; i < n; ++i)

for (int j = 0; j < i; ++j)

if (A[i][0] >= A[j][0] && A[i][1] >= A[j][1] && A[i][2] >= A[j][2])

dp[i] = max(dp[i], dp[j] + A[i][2]);

return *max_element(begin(dp), end(dp));

}

};

Huahua's Tech Road

花花酱 LeetCode 1697. Checking Existence of Edge Length Limited Paths

Solution: Union Find

C++

花花酱 LeetCode 1696. Jump Game VI

Solution: DP + Monotonic Queue

Python3 / TLE

C++

C++/O(n) Space

花花酱 LeetCode 1695. Maximum Erasure Value

Solution: Sliding window + Hashset

C++

花花酱 LeetCode 1694. Reformat Phone Number

Solution:

C++

花花酱 LeetCode 1691. Maximum Height by Stacking Cuboids

Solution: Math/Greedy + DP

C++