Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). Choose a subset of cuboids and place them on each other.
You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. You can rearrange any cuboid’s dimensions by rotating it to put it on another cuboid.
Return the maximum height of the stacked cuboids.
Example 1:
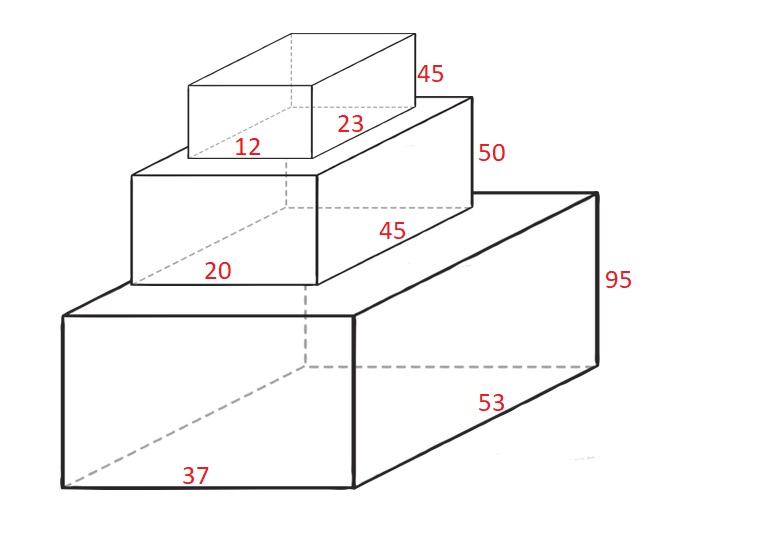
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]] Output: 190 Explanation: Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95. Cuboid 0 is placed next with the 45x20 side facing down with height 50. Cuboid 2 is placed next with the 23x12 side facing down with height 45. The total height is 95 + 50 + 45 = 190.
Example 2:
Input: cuboids = [[38,25,45],[76,35,3]] Output: 76 Explanation: You can't place any of the cuboids on the other. We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.
Example 3:
Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]] Output: 102 Explanation: After rearranging the cuboids, you can see that all cuboids have the same dimension. You can place the 11x7 side down on all cuboids so their heights are 17. The maximum height of stacked cuboids is 6 * 17 = 102.
Constraints:
n == cuboids.length1 <= n <= 1001 <= widthi, lengthi, heighti <= 100
Solution: Math/Greedy + DP
Direct DP is very hard, since there is no orders.
We have to find some way to sort the cuboids such that cuboid i can NOT stack on cuboid j if i > j. Then dp[i] = max(dp[j]) + height[i], 0 <= j < i, for each i, find the best base j and stack on top of it.
ans = max(dp)
We can sort the cuboids by their sorted dimensions, and cuboid i can stack stack onto cuboid j if and only if w[i] <= w[j] and l[i] <= l[j] and h[i] <= h[j].
First of all, we need to prove that all heights must come from the largest dimension of each cuboid.
1. If the top of the stack is A1*A2*A3, A3 < max(A1, A2), we can easily swap A3 with max(A1, A2), it’s still stackable but we get larger heights.
e.g. 3x5x4, base is 3×5, height is 4, we can rotate to get base of 3×4 with height of 5.
2. If a middle cuboid A of size A1*A2*A3, assuming A1 >= A2, A1 > A3, on top of A we have another cuboid B of size B1*B2*B3, B1 <= B2 <= B3.
We have A1 >= B1, A2 >= B2, A3 >= B3, by rotating A we have A3*A2*A1
A3 >= B3 >= B1, A2 >= B2, A1 > A3 >= B3, so B can be still on top of A, and we get larger height.
e.g. A: 3x5x4, B: 2x3x4
A -> 3x4x5, B is still stackable.
…
Time complexity: O(n^2)
Space complexity: O(n^2)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
// Author: Huahua class Solution { public: int maxHeight(vector<vector<int>>& A) { A.push_back({0, 0, 0}); const int n = A.size(); for (auto& box : A) sort(begin(box), end(box)); sort(begin(A), end(A)); vector<int> dp(n); for (int i = 0; i < n; ++i) for (int j = 0; j < i; ++j) if (A[i][0] >= A[j][0] && A[i][1] >= A[j][1] && A[i][2] >= A[j][2]) dp[i] = max(dp[i], dp[j] + A[i][2]); return *max_element(begin(dp), end(dp)); } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment