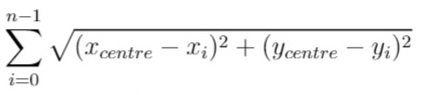Huahua’s Tech Road

花花酱 LeetCode 1678. Goal Parser Interpretation

By zxi on December 5, 2020

You own a Goal Parser that can interpret a string command. The command consists of an alphabet of "G", "()" and/or "(al)" in some order. The Goal Parser will interpret "G" as the string "G", "()" as the string "o", and "(al)" as the string "al". The interpreted strings are then concatenated in the original order.

Given the string command, return the Goal Parser‘s interpretation of command.

Example 1:

Input: command = "G()(al)"
Output: "Goal"
Explanation: The Goal Parser interprets the command as follows:
G -> G
() -> o
(al) -> al
The final concatenated result is "Goal".

Example 2:

Input: command = "G()()()()(al)"
Output: "Gooooal"

Example 3:

Input: command = "(al)G(al)()()G"
Output: "alGalooG"

Constraints:

1 <= command.length <= 100
command consists of "G", "()", and/or "(al)" in some order.

Solution: String

If we encounter ‘(‘ check the next character to determine whether it’s ‘()’ or ‘(al’)

Time complexity: O(n)
Space complexity: O(n)

C++

class Solution {

public:

string interpret(string command) {

string ans;

for (int i = 0; i < command.size(); ++i) {

if (command[i] == 'G') ans += "G";

else if (command[i] == '(') {

if (command[i + 1] == ')') ans += "o";

else ans += "al";

}

return ans;

}

};

Python3

class Solution:

def interpret(self, command: str) -> str:

ans = []

for i, c in enumerate(command):

if c == 'G': ans.append('G')

elif c == '(':

ans.append('o' if command[i + 1] == ')' else 'al')

return ''.join(ans)

花花酱 LeetCode 1515. Best Position for a Service Centre

By zxi on November 30, 2020

A delivery company wants to build a new service centre in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new centre in a position such that the sum of the euclidean distances to all customers is minimum.

Given an array positions where positions[i] = [x_i, y_i] is the position of the ith customer on the map, return the minimum sum of the euclidean distances to all customers.

In other words, you need to choose the position of the service centre [x_centre, y_centre] such that the following formula is minimized:

Answers within 10^-5 of the actual value will be accepted.

Example 1:

Input: positions = [[0,1],[1,0],[1,2],[2,1]]
Output: 4.00000
Explanation: As shown, you can see that choosing [x_centre, y_centre] = [1, 1] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.

Example 2:

Input: positions = [[1,1],[3,3]]
Output: 2.82843
Explanation: The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843

Example 3:

Input: positions = [[1,1]]
Output: 0.00000

Example 4:

Input: positions = [[1,1],[0,0],[2,0]]
Output: 2.73205
Explanation: At the first glance, you may think that locating the centre at [1, 0] will achieve the minimum sum, but locating it at [1, 0] will make the sum of distances = 3.
Try to locate the centre at [1.0, 0.5773502711] you will see that the sum of distances is 2.73205.
Be careful with the precision!

Example 5:

Input: positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
Output: 32.94036
Explanation: You can use [4.3460852395, 4.9813795505] as the position of the centre.

Constraints:

1 <= positions.length <= 50
positions[i].length == 2
0 <= positions[i][0], positions[i][1] <= 100

Solution: Weiszfeld’s algorithm

Use Weiszfeld’s algorithm to compute geometric median of the samples.

Time complexity: O(f(epsilon) * O)
Space complexity: O(1)

C++

template<typename T1, typename T2>

double dist(const vector<T1>& a, const vector<T2>& b) {

return sqrt((a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]));

};

class Solution {

public:

double getMinDistSum(vector<vector<int>>& positions) {

constexpr double kDelta = 1e-7;

constexpr double kEpsilon = 1e-15;

vector<double> c{-1, -1};

double ans = 0;

while (true) {

ans = 0;

double nx = 0, ny = 0;

double denominator = 0;

for (const auto& p : positions) {

double d = dist(c, p) + kEpsilon;

ans += d;

nx += p[0] / d;

ny += p[1] / d;

denominator += 1.0 / d;

}

vector<double> t{nx / denominator, ny / denominator};

if (dist(c, t) < kDelta) return ans;

c = t;

}

return -1;

}

};

花花酱 LeetCode 1286. Iterator for Combination

By zxi on November 30, 2020

Design an Iterator class, which has:

A constructor that takes a string characters of sorted distinct lowercase English letters and a number combinationLength as arguments.
A function next() that returns the next combination of length combinationLength in lexicographical order.
A function hasNext() that returns True if and only if there exists a next combination.

Example:

CombinationIterator iterator = new CombinationIterator("abc", 2); // creates the iterator.

iterator.next(); // returns "ab"
iterator.hasNext(); // returns true
iterator.next(); // returns "ac"
iterator.hasNext(); // returns true
iterator.next(); // returns "bc"
iterator.hasNext(); // returns false

Constraints:

1 <= combinationLength <= characters.length <= 15
There will be at most 10^4 function calls per test.
It’s guaranteed that all calls of the function next are valid.

Solution: Bitmask

Use a bitmask to represent the chars selected.
start with (2^n – 1), decrease the mask until there are c bit set.
stop when mask reach to 0.

mask: 111 => abc
mask: 110 => ab
mask: 101 => ac
mask: 011 => bc
mask: 000 => “” Done

Time complexity: O(2^n)
Space complexity: O(1)

C++

class CombinationIterator {

public:

CombinationIterator(string characters, int combinationLength):

chars_(rbegin(characters), rend(characters)),

length_(combinationLength),

mask_((1 << characters.size()) - 1) {}

string next() {

hasNext();

string ans;

for (int i = chars_.size() - 1; i >= 0 ; --i)

if ((mask_ >> i) & 1)

ans.push_back(chars_[i]);

--mask_;

return ans;

}

bool hasNext() {

while (mask_ >= 0 && __builtin_popcount(mask_) != length_) --mask_;

return mask_ > 0;

}

private:

int mask_ = 0;

const int length_;

const string chars_;

};

花花酱 LeetCode 1675. Minimize Deviation in Array

By zxi on November 29, 2020

You are given an array nums of n positive integers.

You can perform two types of operations on any element of the array any number of times:

If the element is even, divide it by 2.
- For example, if the array is [1,2,3,4], then you can do this operation on the last element, and the array will be [1,2,3,2].
If the element is odd, multiply it by 2.
- For example, if the array is [1,2,3,4], then you can do this operation on the first element, and the array will be [2,2,3,4].

The deviation of the array is the maximum difference between any two elements in the array.

Return the minimum deviation the array can have after performing some number of operations.

Example 1:

Input: nums = [1,2,3,4]
Output: 1
Explanation: You can transform the array to [1,2,3,2], then to [2,2,3,2], then the deviation will be 3 - 2 = 1.

Example 2:

Input: nums = [4,1,5,20,3]
Output: 3
Explanation: You can transform the array after two operations to [4,2,5,5,3], then the deviation will be 5 - 2 = 3.

Example 3:

Input: nums = [2,10,8]
Output: 3

Constraints:

n == nums.length
2 <= n <= 10⁵
1 <= nums[i] <= 10⁹

Solution: Priority Queue

If we double an odd number it becomes an even number, then we can only divide it by two which gives us back the original number. So we can pre-double all the odd numbers and only do division in the following process.

We push all numbers including pre-doubled odd ones onto a priority queue, and track the difference between the largest and smallest number.

Each time, we pop the largest number out and divide it by two then put it back to the priority queue, until the largest number becomes odd. We can not discard it and divide any other smaller numbers by two will only increase the max difference, so we can stop here.

ex1: [3, 5, 8] => [6, 8, 10] (pre-double) => [5, 6, 8] => [4, 5, 6] => [3, 4, 5] max diff is 5 – 3 = 2
ex2: [4,1,5,20,3] => [2, 4, 6, 10, 20] (pre-double) => [2, 4, 6, 10] => [2, 4, 5, 6] => [2,3,4,5] max diff = 5-2 = 3

Time complexity: O(n*logm*logn)
Space complexity: O(n)

C++/Set

class Solution {

public:

int minimumDeviation(vector<int>& nums) {

set<int> s;

for (int x : nums)

s.insert(x & 1 ? x * 2 : x);

int ans = *rbegin(s) - *begin(s);

while (*rbegin(s) % 2 == 0) {

s.insert(*rbegin(s) / 2);

s.erase(*rbegin(s));

ans = min(ans, *rbegin(s) - *begin(s));

}

return ans;

}

};

C++/PQ

class Solution {

public:

int minimumDeviation(vector<int>& nums) {

priority_queue<int> q;

int lo = INT_MAX;

for (int x : nums) {

x = x & 1 ? x * 2 : x;

q.push(x);

lo = min(lo, x);

}

int ans = q.top() - lo;

while (q.top() % 2 == 0) {

int x = q.top(); q.pop();

q.push(x / 2);

lo = min(lo, x / 2);

ans = min(ans, q.top() - lo);

}

return ans;

}

};

花花酱 LeetCode 1674. Minimum Moves to Make Array Complementary

By zxi on November 29, 2020

You are given an integer array nums of even length n and an integer limit. In one move, you can replace any integer from nums with another integer between 1 and limit, inclusive.

The array nums is complementary if for all indices i (0-indexed), nums[i] + nums[n - 1 - i] equals the same number. For example, the array [1,2,3,4] is complementary because for all indices i, nums[i] + nums[n - 1 - i] = 5.

Return the minimum number of moves required to make nums complementary.

Example 1:

Input: nums = [1,2,4,3], limit = 4
Output: 1
Explanation: In 1 move, you can change nums to [1,2,2,3] (underlined elements are changed).
nums[0] + nums[3] = 1 + 3 = 4.
nums[1] + nums[2] = 2 + 2 = 4.
nums[2] + nums[1] = 2 + 2 = 4.
nums[3] + nums[0] = 3 + 1 = 4.
Therefore, nums[i] + nums[n-1-i] = 4 for every i, so nums is complementary.

Example 2:

Input: nums = [1,2,2,1], limit = 2
Output: 2
Explanation: In 2 moves, you can change nums to [2,2,2,2]. You cannot change any number to 3 since 3 > limit.

Example 3:

Input: nums = [1,2,1,2], limit = 2
Output: 0
Explanation: nums is already complementary.

Constraints:

n == nums.length
2 <= n <= 10⁵
1 <= nums[i] <= limit <= 10⁵
n is even.

Solution: Sweep Line / Prefix Sum

Let a = min(nums[i], nums[n-i-1]), b = max(nums[i], nums[n-i-1])
The key to this problem is how many moves do we need to make a + b == T.

if 2 <= T < a + 1, two moves, lower both a and b.
if a +1 <= T < a + b, one move, lower b
if a + b == T, zero move
if a + b + 1 <= T < b + limit + 1, one move, increase a
if b + limit + 1 <= T <= 2*limit, two moves, increase both a and b.

Time complexity: O(n + limit) or O(nlogn) if limit >>n
Space complexity: O(limit) or O(n)

C++

// Author: Huahua

class Solution {

public:

int minMoves(vector<int>& nums, int limit) {

const int n = nums.size();

vector<int> delta(limit * 2 + 2);

for (int i = 0; i < n / 2; ++i) {

const int a = min(nums[i], nums[n - i - 1]);

const int b = max(nums[i], nums[n - i - 1]);

delta[2] += 2; // dec a, dec b

--delta[a + 1]; // dec a

--delta[a + b]; // no op

++delta[a + b + 1]; // inc a

++delta[b + limit + 1]; // inc a, inc b

}

int ans = n;

for (int t = 2, cur = 0; t <= limit * 2; ++t) {

cur += delta[t];

ans = min(ans, cur);

}

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1678. Goal Parser Interpretation

Solution: String

C++

Python3

花花酱 LeetCode 1515. Best Position for a Service Centre

Solution: Weiszfeld’s algorithm

C++

花花酱 LeetCode 1286. Iterator for Combination

Solution: Bitmask

C++

花花酱 LeetCode 1675. Minimize Deviation in Array

Solution: Priority Queue

C++/Set

C++/PQ

花花酱 LeetCode 1674. Minimum Moves to Make Array Complementary

Solution: Sweep Line / Prefix Sum

C++