Huahua’s Tech Road

花花酱 LeetCode 1605. Find Valid Matrix Given Row and Column Sums

By zxi on October 3, 2020

You are given two arrays rowSum and colSum of non-negative integers where rowSum[i] is the sum of the elements in the i^th row and colSum[j] is the sum of the elements of the j^th column of a 2D matrix. In other words, you do not know the elements of the matrix, but you do know the sums of each row and column.

Find any matrix of non-negative integers of size rowSum.length x colSum.length that satisfies the rowSum and colSum requirements.

Return a 2D array representing any matrix that fulfills the requirements. It’s guaranteed that at least one matrix that fulfills the requirements exists.

Example 1:

Input: rowSum = [3,8], colSum = [4,7]
Output: [[3,0],
         [1,7]]
Explanation:
0th row: 3 + 0 = 0 == rowSum[0]
1st row: 1 + 7 = 8 == rowSum[1]
0th column: 3 + 1 = 4 == colSum[0]
1st column: 0 + 7 = 7 == colSum[1]
The row and column sums match, and all matrix elements are non-negative.
Another possible matrix is: [[1,2],
                             [3,5]]

Example 2:

Input: rowSum = [5,7,10], colSum = [8,6,8]
Output: [[0,5,0],
         [6,1,0],
         [2,0,8]]

Example 3:

Input: rowSum = [14,9], colSum = [6,9,8]
Output: [[0,9,5],
         [6,0,3]]

Example 4:

Input: rowSum = [1,0], colSum = [1]
Output: [[1],
         [0]]

Example 5:

Input: rowSum = [0], colSum = [0]
Output: [[0]]

Constraints:

1 <= rowSum.length, colSum.length <= 500
0 <= rowSum[i], colSum[i] <= 10⁸
sum(rows) == sum(columns)

Solution: Greedy

Let a = min(row[i], col[j]), m[i][j] = a, row[i] -= a, col[j] -=a

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> restoreMatrix(vector<int>& rowSum, vector<int>& colSum) {

const int m = rowSum.size();

const int n = colSum.size();

vector<vector<int>> ans(m, vector<int>(n));

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j) {

ans[i][j] = min(rowSum[i], colSum[j]);

rowSum[i] -= ans[i][j];

colSum[j] -= ans[i][j];

}

return ans;

}

};

花花酱 LeetCode 1604. Alert Using Same Key-Card Three or More Times in a One Hour Period

By zxi on October 3, 2020

Leetcode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker’s name and the time when it was used. The system emits an alert if any worker uses the key-card three or more times in a one-hour period.

You are given a list of strings keyName and keyTime where [keyName[i], keyTime[i]] corresponds to a person’s name and the time when their key-card was used in a single day.

Access times are given in the 24-hour time format “HH:MM”, such as "23:51" and "09:49".

Return a list of unique worker names who received an alert for frequent keycard use. Sort the names in ascending order alphabetically.

Notice that "10:00" – "11:00" is considered to be within a one-hour period, while "23:51" – "00:10" is not considered to be within a one-hour period.

Example 1:

Input: keyName = ["daniel","daniel","daniel","luis","luis","luis","luis"], keyTime = ["10:00","10:40","11:00","09:00","11:00","13:00","15:00"]
Output: ["daniel"]
Explanation: "daniel" used the keycard 3 times in a one-hour period ("10:00","10:40", "11:00").

Example 2:

Input: keyName = ["alice","alice","alice","bob","bob","bob","bob"], keyTime = ["12:01","12:00","18:00","21:00","21:20","21:30","23:00"]
Output: ["bob"]
Explanation: "bob" used the keycard 3 times in a one-hour period ("21:00","21:20", "21:30").

Example 3:

Input: keyName = ["john","john","john"], keyTime = ["23:58","23:59","00:01"]
Output: []

Example 4:

Input: keyName = ["leslie","leslie","leslie","clare","clare","clare","clare"], keyTime = ["13:00","13:20","14:00","18:00","18:51","19:30","19:49"]
Output: ["clare","leslie"]

Constraints:

1 <= keyName.length, keyTime.length <= 10⁵
keyName.length == keyTime.length
keyTime are in the format “HH:MM”.
[keyName[i], keyTime[i]] is unique.
1 <= keyName[i].length <= 10
keyName[i] contains only lowercase English letters.

Solution: Hashtable + sorting

Time complexity: O(nlogn)
Space complexity: O(n)

C++

class Solution {

public:

vector<string> alertNames(vector<string>& keyName, vector<string>& keyTime) {

unordered_map<string, vector<int>> t; // {name -> time}

for (size_t i = 0; i < keyName.size(); ++i) {

const int h = stoi(keyTime[i].substr(0, 2));

const int m = stoi(keyTime[i].substr(3));

t[keyName[i]].push_back(h * 60 + m);

}

vector<string> ans;

for (auto& [name, times] : t) {

sort(begin(times), end(times));

for (size_t i = 2; i < times.size(); ++i)

if (times[i] - times[i - 2] <= 60) {

ans.push_back(name);

break;

}

sort(begin(ans), end(ans));

return ans;

}

};

花花酱 LeetCode 1603. Design Parking System

By zxi on October 3, 2020

Design a parking system for a parking lot. The parking lot has three kinds of parking spaces: big, medium, and small, with a fixed number of slots for each size.

Implement the ParkingSystem class:

ParkingSystem(int big, int medium, int small) Initializes object of the ParkingSystem class. The number of slots for each parking space are given as part of the constructor.
bool addCar(int carType) Checks whether there is a parking space of carType for the car that wants to get into the parking lot. carType can be of three kinds: big, medium, or small, which are represented by 1, 2, and 3 respectively. A car can only park in a parking space of its carType. If there is no space available, return false, else park the car in that size space and return true.

Example 1:

Input
["ParkingSystem", "addCar", "addCar", "addCar", "addCar"]
[[1, 1, 0], [1], [2], [3], [1]]
Output
[null, true, true, false, false]

Explanation ParkingSystem parkingSystem = new ParkingSystem(1, 1, 0); parkingSystem.addCar(1); // return true because there is 1 available slot for a big car parkingSystem.addCar(2); // return true because there is 1 available slot for a medium car parkingSystem.addCar(3); // return false because there is no available slot for a small car parkingSystem.addCar(1); // return false because there is no available slot for a big car. It is already occupied.

Constraints:

0 <= big, medium, small <= 1000
carType is 1, 2, or 3
At most 1000 calls will be made to addCar

Solution: Simulation

Time complexity: O(1) per addCar call
Space complexity: O(1)

C++

// Author: Huahua

class ParkingSystem {

public:

ParkingSystem(int big, int medium, int small):

slots_{{big, medium, small}} {}

bool addCar(int carType) {

return slots_[carType - 1]-- > 0;

}

private:

vector<int> slots_;

};

Python3

# Author: Huahua

class ParkingSystem:

def __init__(self, big: int, medium: int, small: int):

self.slots = {1: big, 2: medium, 3: small}

def addCar(self, carType: int) -> bool:

if self.slots[carType] == 0: return False

self.slots[carType] -= 1

return True

花花酱 LeetCode 1601. Maximum Number of Achievable Transfer Requests

By zxi on September 27, 2020

We have n buildings numbered from 0 to n - 1. Each building has a number of employees. It’s transfer season, and some employees want to change the building they reside in.

You are given an array requests where requests[i] = [from_i, to_i] represents an employee’s request to transfer from building from_i to building to_i.

All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.

Return the maximum number of achievable requests.

Example 1:

Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
Output: 5
Explantion: Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.

Example 2:

Input: n = 3, requests = [[0,0],[1,2],[2,1]]
Output: 3
Explantion: Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests.

Example 3:

Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
Output: 4

Constraints:

1 <= n <= 20
1 <= requests.length <= 16
requests[i].length == 2
0 <= from_i, to_i < n

Solution: Combination

Try all combinations: O(2^n * (r + n))
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maximumRequests(int n, vector<vector<int>>& requests) {

const int r = requests.size();

int ans = 0;

vector<int> nets(n);

for (int s = 0; s < 1 << r; ++s) {

fill(begin(nets), end(nets), 0);

for (int j = 0; j < r; ++j)

if (s & (1 << j)) {

--nets[requests[j][0]];

++nets[requests[j][1]];

}

if (all_of(begin(nets), end(nets), [](const int x) { return x == 0; }))

ans = max(ans, __builtin_popcount(s));

}

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def maximumRequests(self, n: int, requests: List[List[int]]) -> int:

r = len(requests)

ans = 0

for s in range(1 << r):

degrees = [0] * n

for i in range(r):

if s & (1 << i):

degrees[requests[i][0]] -= 1

degrees[requests[i][1]] += 1

if not any(degrees):

ans = max(ans, bin(s).count('1'))

return ans

花花酱 LeetCode 1600. Throne Inheritance

By zxi on September 27, 2020

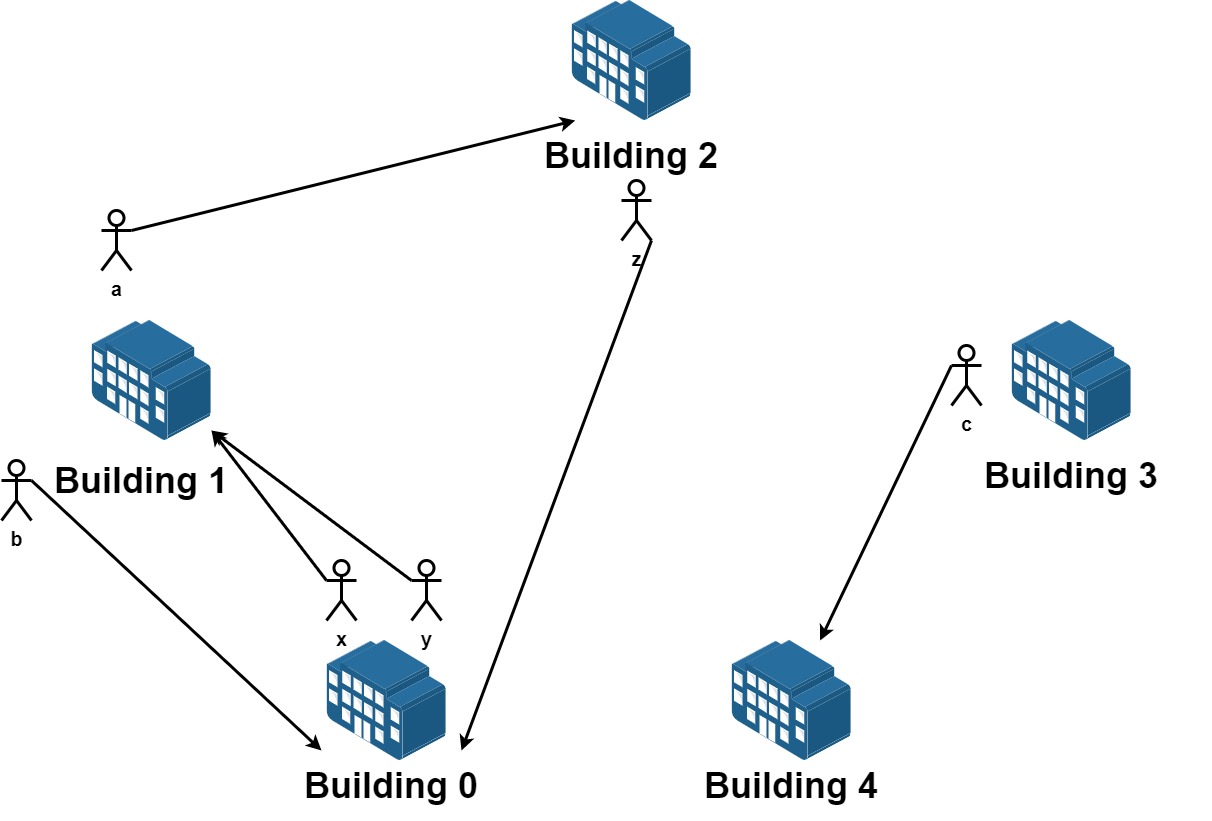
A kingdom consists of a king, his children, his grandchildren, and so on. Every once in a while, someone in the family dies or a child is born.

The kingdom has a well-defined order of inheritance that consists of the king as the first member. Let’s define the recursive function Successor(x, curOrder), which given a person x and the inheritance order so far, returns who should be the next person after x in the order of inheritance.

Successor(x, curOrder):

if x has no children or all of x's children are in curOrder:

if x is the king return null

else return Successor(x's parent, curOrder)

else return x's oldest child who's not in curOrder

For example, assume we have a kingdom that consists of the king, his children Alice and Bob (Alice is older than Bob), and finally Alice’s son Jack.

In the beginning, curOrder will be ["king"].
Calling Successor(king, curOrder) will return Alice, so we append to curOrder to get ["king", "Alice"].
Calling Successor(Alice, curOrder) will return Jack, so we append to curOrder to get ["king", "Alice", "Jack"].
Calling Successor(Jack, curOrder) will return Bob, so we append to curOrder to get ["king", "Alice", "Jack", "Bob"].
Calling Successor(Bob, curOrder) will return null. Thus the order of inheritance will be ["king", "Alice", "Jack", "Bob"].

Using the above function, we can always obtain a unique order of inheritance.

Implement the ThroneInheritance class:

ThroneInheritance(string kingName) Initializes an object of the ThroneInheritance class. The name of the king is given as part of the constructor.
void birth(string parentName, string childName) Indicates that parentName gave birth to childName.
void death(string name) Indicates the death of name. The death of the person doesn’t affect the Successor function nor the current inheritance order. You can treat it as just marking the person as dead.
string[] getInheritanceOrder() Returns a list representing the current order of inheritance excluding dead people.

Example 1:

Input
["ThroneInheritance", "birth", "birth", "birth", "birth", "birth", "birth", "getInheritanceOrder", "death", "getInheritanceOrder"]
[["king"], ["king", "andy"], ["king", "bob"], ["king", "catherine"], ["andy", "matthew"], ["bob", "alex"], ["bob", "asha"], [null], ["bob"], [null]]
Output
[null, null, null, null, null, null, null, ["king", "andy", "matthew", "bob", "alex", "asha", "catherine"], null, ["king", "andy", "matthew", "alex", "asha", "catherine"]]
Explanation
ThroneInheritance t= new ThroneInheritance("king"); // order: king
t.birth("king", "andy"); // order: king > andy
t.birth("king", "bob"); // order: king > andy > bob
t.birth("king", "catherine"); // order: king > andy > bob > catherine
t.birth("andy", "matthew"); // order: king > andy > matthew > bob > catherine
t.birth("bob", "alex"); // order: king > andy > matthew > bob > alex > catherine
t.birth("bob", "asha"); // order: king > andy > matthew > bob > alex > asha > catherine
t.getInheritanceOrder(); // return ["king", "andy", "matthew", "bob", "alex", "asha", "catherine"]
t.death("bob"); // order: king > andy > matthew > bob > alex > asha > catherine
t.getInheritanceOrder(); // return ["king", "andy", "matthew", "alex", "asha", "catherine"]

Constraints:

1 <= kingName.length, parentName.length, childName.length, name.length <= 15
kingName, parentName, childName, and name consist of lowercase English letters only.
All arguments childName and kingName are distinct.
All name arguments of death will be passed to either the constructor or as childName to birth first.
For each call to birth(parentName, childName), it is guaranteed that parentName is alive.
At most 10⁵ calls will be made to birth and death.
At most 10 calls will be made to getInheritanceOrder.

Solution: HashTable + DFS

Record :
1. mapping from parent to children (ordered)
2. who has dead

Time complexity: getInheritanceOrder O(n), other O(1)
Space complexity: O(n)

C++

// Author: Huahua

class ThroneInheritance {

public:

ThroneInheritance(string kingName): king_(kingName) {

m_[kingName] = {};

}

void birth(string parentName, string childName) {

m_[parentName].push_back(childName);

}

void death(string name) {

dead_.insert(name);

}

vector<string> getInheritanceOrder() {

vector<string> ans;

function<void(const string&)> dfs = [&](const string& name) {

if (!dead_.count(name)) ans.push_back(name);

for (const string& child: m_[name]) dfs(child);

};

dfs(king_);

return ans;

}

private:

string king_;

unordered_map<string, vector<string>> m_; // parent -> list[children]

unordered_set<string> dead_;

};

Python3

# Author: Huahua

class ThroneInheritance:

def __init__(self, kingName: str):

self.kingName = kingName

self.family = defaultdict(list)

self.dead = set()

def birth(self, parentName: str, childName: str) -> None:

self.family[parentName].append(childName)

def death(self, name: str) -> None:

self.dead.add(name)

def getInheritanceOrder(self) -> List[str]:

order = []

def dfs(name: str):

if name not in self.dead: order.append(name)

for child in self.family[name]: dfs(child)

dfs(self.kingName)

return order

Huahua's Tech Road

花花酱 LeetCode 1605. Find Valid Matrix Given Row and Column Sums

Solution: Greedy

C++

花花酱 LeetCode 1604. Alert Using Same Key-Card Three or More Times in a One Hour Period

Solution: Hashtable + sorting

C++

花花酱 LeetCode 1603. Design Parking System

Solution: Simulation

C++

Python3

花花酱 LeetCode 1601. Maximum Number of Achievable Transfer Requests

Solution: Combination

C++

Python3

花花酱 LeetCode 1600. Throne Inheritance

Solution: HashTable + DFS

C++

Python3