Huahua’s Tech Road

花花酱 LeetCode 1559. Detect Cycles in 2D Grid

By zxi on August 23, 2020

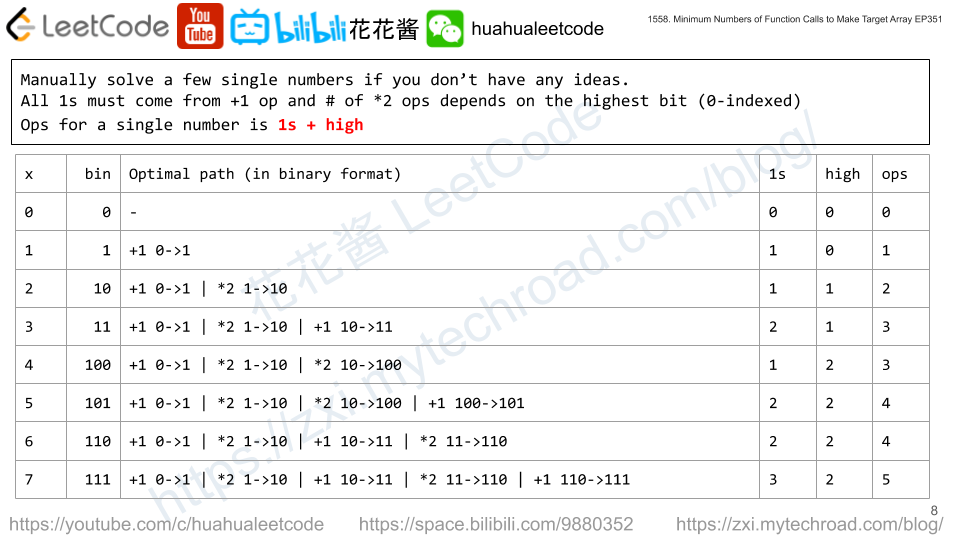
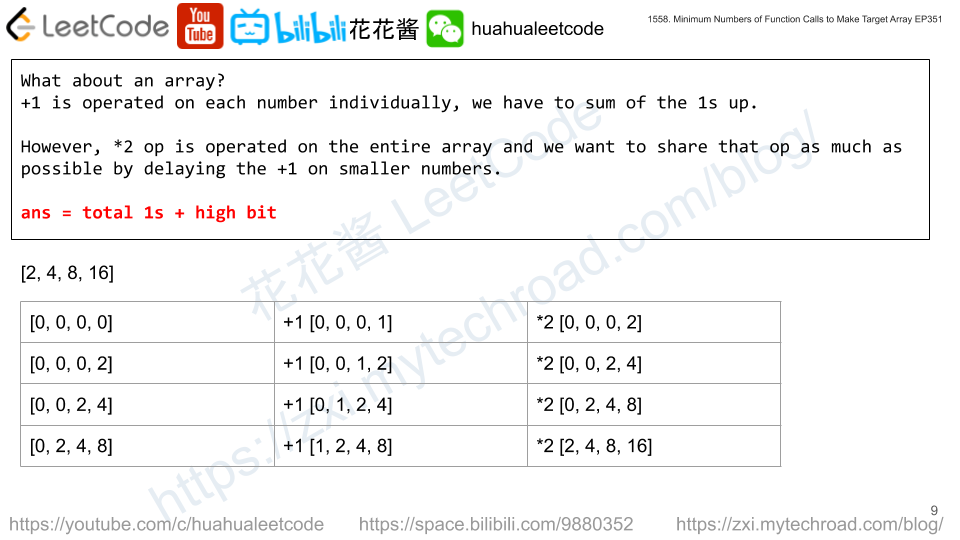
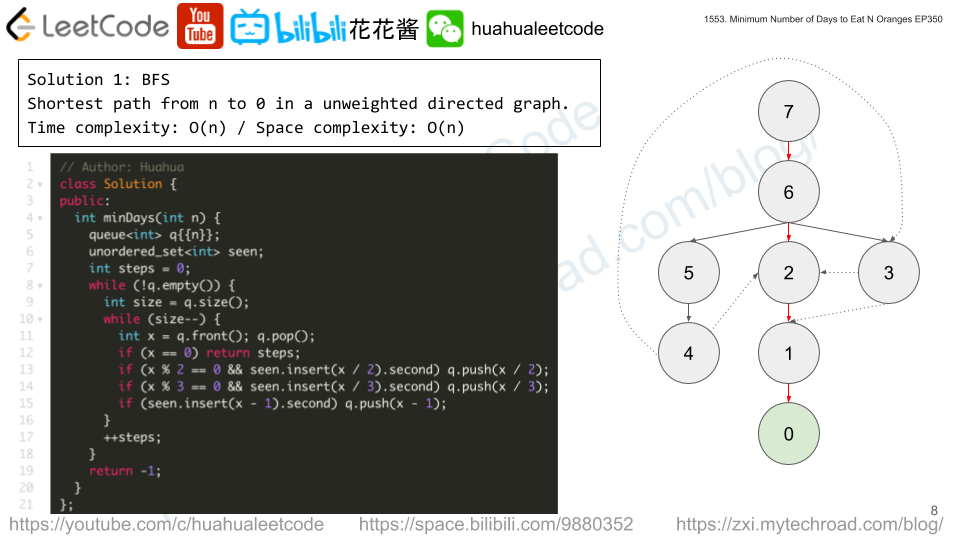
Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.

A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it – in one of the four directions (up, down, left, or right), if it has the same value of the current cell.

Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.

Return true if any cycle of the same value exists in grid, otherwise, return false.

Example 1:

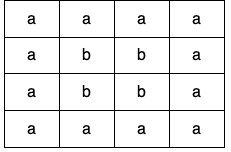
Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below:

Example 2:

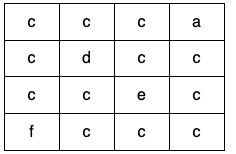
Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below:

Example 3:

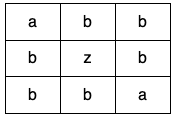
Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false

Constraints:

m == grid.length
n == grid[i].length
1 <= m <= 500
1 <= n <= 500
grid consists only of lowercase English letters.

Solution: DFS

Finding a cycle in an undirected graph => visiting a node that has already been visited and it’s not the parent node of the current node.
b b
b b
null -> (0, 0) -> (0, 1) -> (1, 1) -> (1, 0) -> (0, 0)
The second time we visit (0, 0) which has already been visited before and it’s not the parent of the current node (1, 0) ( (1, 0)’s parent is (1, 1) ) which means we found a cycle.

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

class Solution {

public:

bool containsCycle(vector<vector<char>>& grid) {

const int m = grid.size();

const int n = grid[0].size();

vector<vector<int>> seen(m, vector<int>(n));

vector<int> dirs{0, 1, 0, -1, 0};

function<bool(int, int, int, int)> dfs = [&](int i, int j, int pi, int pj) {

++seen[i][j];

for (int d = 0; d < 4; ++d) {

int ni = i + dirs[d];

int nj = j + dirs[d + 1];

if (ni < 0 || nj < 0 || ni >= m || nj >= n) continue;

if (grid[ni][nj] != grid[i][j]) continue;

if (!seen[ni][nj]) {

if (dfs(ni, nj, i, j)) return true;

} else if (ni != pi || nj != pj) {

return true;

}

return false;

};

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

if (!seen[i][j]++ && dfs(i, j, -1, -1))

return true;

return false;

}

};

花花酱 LeetCode 1558. Minimum Numbers of Function Calls to Make Target Array

By zxi on August 22, 2020

Your task is to form an integer array nums from an initial array of zeros arr that is the same size as nums.

Return the minimum number of function calls to make nums from arr.

The answer is guaranteed to fit in a 32-bit signed integer.

Example 1:

Input: nums = [1,5]
Output: 5
Explanation: Increment by 1 (second element): [0, 0] to get [0, 1] (1 operation).
Double all the elements: [0, 1] -> [0, 2] -> [0, 4] (2 operations).
Increment by 1 (both elements)  [0, 4] -> [1, 4] -> [1, 5] (2 operations).
Total of operations: 1 + 2 + 2 = 5.

Example 2:

Input: nums = [2,2]
Output: 3
Explanation: Increment by 1 (both elements) [0, 0] -> [0, 1] -> [1, 1] (2 operations).
Double all the elements: [1, 1] -> [2, 2] (1 operation).
Total of operations: 2 + 1 = 3.

Example 3:

Input: nums = [4,2,5]
Output: 6
Explanation: (initial)[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5](nums).

Example 4:

Input: nums = [3,2,2,4]
Output: 7

Example 5:

Input: nums = [2,4,8,16]
Output: 8

Constraints:

1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9

Solution: count 1s

For 5 (101b), we can add 1s for 5 times which of cause isn’t the best way to generate 5, the optimal way is to [+1, *2, +1]. We have to add 1 for each 1 in the binary format. e.g. 11 (1011), we need 3x “+1” op, and 4 “*2” op. Fortunately, the “*2” can be shared/delayed, thus we just need to find the largest number.
e.g. [2,4,8,16]
[0, 0, 0, 0] -> [0, 0, 0, 1] -> [0, 0, 0, 2]
[0, 0, 0, 2] -> [0, 0, 1, 2] -> [0, 0, 2, 4]
[0, 0, 2, 4] -> [0, 1, 2, 4] -> [0, 2, 4, 8]
[0, 2, 4, 8] -> [1, 2, 4, 8] -> [2, 4, 8, 16]
ans = sum{count_1(arr_i)} + high_bit(max(arr_i))

Time complexity: O(n*log(max(arr_i))
Space complexity: O(1)

C++

class Solution {

public:

int minOperations(vector<int>& nums) {

int ans = 0;

int high = 0;

for (int x : nums) {

high = max(high, 31 - __builtin_clz(x | 1));

ans += std::bitset<32>(x).count();

}

return ans + high;

}

};

Java

class Solution {

public int minOperations(int[] nums) {

int ans = 0;

int high = 0;

for (int x : nums) {

int l = -1;

while (x != 0) {

ans += x & 1;

x >>= 1;

++l;

}

high = Math.max(high, l);

}

return ans + high;

}

Python3

class Solution:

def minOperations(self, nums: List[int]) -> int:

return sum(bin(x).count('1') for x in nums) + len(bin(max(nums))) - 3

花花酱 LeetCode 1557. Minimum Number of Vertices to Reach All Nodes

By zxi on August 22, 2020

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [from_i, to_i] represents a directed edge from node from_i to node to_i.

Find the smallest set of vertices from which all nodes in the graph are reachable. It’s guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:

Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= from_i, to_i < n
All pairs (from_i, to_i) are distinct.

Solution: In degree

Nodes with 0 in degree will be the answer.
Time complexity: O(E+V)
Space complexity: O(V)

C++

class Solution {

public:

vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {

vector<int> in(n);

for (const auto& e : edges) ++in[e[1]];

vector<int> ans;

for (int i = 0; i < n; ++i)

if (in[i] == 0) ans.push_back(i);

return ans;

}

};

花花酱 LeetCode 1556. Thousand Separator

By zxi on August 22, 2020

Given an integer n, add a dot (“.”) as the thousands separator and return it in string format.

Example 1:

Input: n = 987
Output: "987"

Example 2:

Input: n = 1234
Output: "1.234"

Example 3:

Input: n = 123456789
Output: "123.456.789"

Example 4:

Input: n = 0
Output: "0"

Constraints:

0 <= n < 2^31

Solution: Digit by digit

Time complexity: O(log^2(n)) -> O(logn)
Space complexity: O(log(n))

C++

class Solution {

public:

string thousandSeparator(int n) {

string ans;

int count = 0;

do {

if (count++ % 3 == 0 && ans.size())

ans = "." + ans;

ans = to_string(n % 10) + ans;

n /= 10;

} while (n);

return ans;

}

};

花花酱 LeetCode 1553. Minimum Number of Days to Eat N Oranges

By zxi on August 16, 2020

There are n oranges in the kitchen and you decided to eat some of these oranges every day as follows:

Eat one orange.
If the number of remaining oranges (n) is divisible by 2 then you can eat n/2 oranges.
If the number of remaining oranges (n) is divisible by 3 then you can eat 2*(n/3) oranges.

You can only choose one of the actions per day.

Return the minimum number of days to eat n oranges.

Example 1:

Input: n = 10
Output: 4
Explanation: You have 10 oranges.
Day 1: Eat 1 orange,  10 - 1 = 9.  
Day 2: Eat 6 oranges, 9 - 2*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2*(3/3) = 3 - 2 = 1. 
Day 4: Eat the last orange  1 - 1  = 0.
You need at least 4 days to eat the 10 oranges.

Example 2:

Input: n = 6
Output: 3
Explanation: You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange  1 - 1  = 0.
You need at least 3 days to eat the 6 oranges.

Example 3:

Input: n = 1
Output: 1

Example 4:

Input: n = 56
Output: 6

Constraints:

1 <= n <= 2*10^9

Solution: Greedy + DP

Eat oranges one by one to make it a multiply of 2 or 3 such that we can eat 50% or 66.66…% of the oranges in one step.
dp(n) := min steps to finish n oranges.
base case n <= 1, dp(n) = n
transition: dp(n) = 1 + min(n%2 + dp(n/2), n % 3 + dp(n / 3))
e.g. n = 11,
we eat 11%2 = 1 in one step, left = 10 and then eat 10 / 2 = 5 in another step. 5 left for the subproblem.
we eat 11%3 = 2 in two steps, left = 9 and then eat 9 * 2 / 3 = 6 in another step, 3 left for the subproblem.
dp(11) = 1 + min(1 + dp(5), 2 + dp(3))

T(n) = 2*T(n/2) + O(1) = O(n)
Time complexity: O(n) // w/o memoization, close to O(logn) in practice.
Space complexity: O(logn)

C++

class Solution {

public:

int minDays(int n) {

unordered_map<int, int> cache;

function<int(int)> dp = [&](int n) {

if (n <= 1) return n;

auto it = cache.find(n);

if (it != cache.end()) return it->second;

return cache[n] = 1 + min(n % 2 + dp(n / 2), n % 3 + dp(n / 3));

};

return dp(n);

}

};

Java

class Solution {

private static Map<Integer, Integer> cache = new HashMap<>();

public int minDays(int n) {

return dp(n);

}

private int dp(int n) {

if (n <= 1) return n;

if (cache.containsKey(n)) return cache.get(n);

int ans = 1 + Math.min(n % 2 + dp(n / 2), n % 3 + dp(n / 3));

cache.put(n, ans);

return ans;

}

Python3

class Solution:

def minDays(self, n: int) -> int:

@lru_cache(None)

def dp(n):

if n <= 1: return n

return 1 + min(n % 2 + dp(n // 2), n % 3 + dp(n // 3))

return dp(n)

Solution 2: BFS

if x % 2 == 0, push x/2 onto the queue
if x % 3 == 0, push x/3 onto the queue
always push x – 1 onto the queue

C++

class Solution {

public:

int minDays(int n) {

queue<int> q{{n}};

unordered_set<int> seen;

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

int x = q.front(); q.pop();

if (x == 0) return steps;

if (x % 2 == 0 && seen.insert(x / 2).second)

q.push(x / 2);

if (x % 3 == 0 && seen.insert(x / 3).second)

q.push(x / 3);

if (seen.insert(x - 1).second)

q.push(x - 1);

}

++steps;

}

return -1;

}

};

Huahua's Tech Road

花花酱 LeetCode 1559. Detect Cycles in 2D Grid

Solution: DFS

C++

花花酱 LeetCode 1558. Minimum Numbers of Function Calls to Make Target Array

Solution: count 1s

C++

Java

Python3

花花酱 LeetCode 1557. Minimum Number of Vertices to Reach All Nodes

Solution: In degree

C++

花花酱 LeetCode 1556. Thousand Separator

C++

花花酱 LeetCode 1553. Minimum Number of Days to Eat N Oranges

Solution: Greedy + DP

C++

Java

Python3

Solution 2: BFS

C++