Huahua's Tech Road

花花酱 LeetCode 1377. Frog Position After T Seconds

By zxi on March 8, 2020

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [from_i, to_i] means that exists an edge connecting directly the vertices from_i and to_i.

Return the probability that after t seconds the frog is on the vertex target.

Example 1:

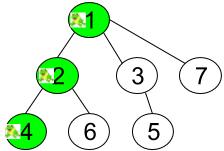
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.

Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.

Example 3:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

1 <= n <= 100
edges.length == n-1
edges[i].length == 2
1 <= edges[i][0], edges[i][1] <= n
1 <= t <= 50
1 <= target <= n
Answers within 10^-5 of the actual value will be accepted as correct.

Solution: BFS

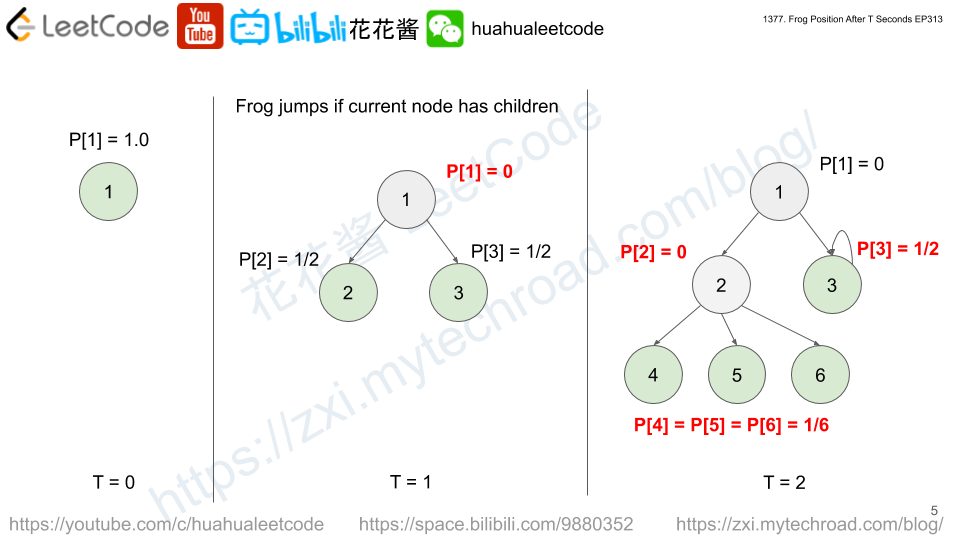
key: if a node has children, the fog jumps to to children so the probability at current node will become 0.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {

vector<double> p(n + 1);

p[1] = 1.0;

vector<vector<int>> g(n + 1);

for (const auto& e : edges) {

g[e[0]].push_back(e[1]);

g[e[1]].push_back(e[0]);

}

vector<int> seen(n + 1);

seen[1] = 1;

queue<int> q{{1}};

while (t--) {

int size = q.size();

while (size--) {

int cur = q.front(); q.pop();

int children = 0;

for (int nxt : g[cur])

if (!seen[nxt]) ++children;

for (int nxt : g[cur])

if (!seen[nxt]++) {

q.push(nxt);

p[nxt] += p[cur] / children;

}

// key: fog jumps this node has children

if (children > 0) p[cur] = 0.0;

}

return p[target];

}

};

python3

class Solution:

def frogPosition(self, n: int, edges: List[List[int]],

t: int, target: int) -> float:

p = [0] + [1] + [0] * (n - 1)

seen = [False] + [True] + [False] * (n - 1)

q = [1]

g = [[] for _ in range(n + 1)]

for i, j in edges:

g[i].append(j)

g[j].append(i)

for _ in range(t):

q2 = []

for cur in q:

children = sum([not seen[nxt] for nxt in g[cur]])

for nxt in g[cur]:

if seen[nxt]: continue

seen[nxt] = True

q2.append(nxt)

p[nxt] = p[cur] / children

if children > 0: p[cur] = 0

q = q2

return p[target]

花花酱 LeetCode 1376. Time Needed to Inform All Employees

By zxi on March 8, 2020

A company has n employees with a unique ID for each employee from 0 to n - 1. The head of the company has is the one with headID.

Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also it’s guaranteed that the subordination relationships have a tree structure.

The head of the company wants to inform all the employees of the company of an urgent piece of news. He will inform his direct subordinates and they will inform their subordinates and so on until all employees know about the urgent news.

The i-th employee needs informTime[i] minutes to inform all of his direct subordinates (i.e After informTime[i] minutes, all his direct subordinates can start spreading the news).

Return the number of minutes needed to inform all the employees about the urgent news.

Example 1:

Input: n = 1, headID = 0, manager = [-1], informTime = [0]
Output: 0
Explanation: The head of the company is the only employee in the company.

Example 2:

Input: n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
Output: 1
Explanation: The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.

Example 3:

Input: n = 7, headID = 6, manager = [1,2,3,4,5,6,-1], informTime = [0,6,5,4,3,2,1]
Output: 21
Explanation: The head has id = 6. He will inform employee with id = 5 in 1 minute.
The employee with id = 5 will inform the employee with id = 4 in 2 minutes.
The employee with id = 4 will inform the employee with id = 3 in 3 minutes.
The employee with id = 3 will inform the employee with id = 2 in 4 minutes.
The employee with id = 2 will inform the employee with id = 1 in 5 minutes.
The employee with id = 1 will inform the employee with id = 0 in 6 minutes.
Needed time = 1 + 2 + 3 + 4 + 5 + 6 = 21.

Example 4:

Input: n = 15, headID = 0, manager = [-1,0,0,1,1,2,2,3,3,4,4,5,5,6,6], informTime = [1,1,1,1,1,1,1,0,0,0,0,0,0,0,0]
Output: 3
Explanation: The first minute the head will inform employees 1 and 2.
The second minute they will inform employees 3, 4, 5 and 6.
The third minute they will inform the rest of employees.

Example 5:

Input: n = 4, headID = 2, manager = [3,3,-1,2], informTime = [0,0,162,914]
Output: 1076

Constraints:

1 <= n <= 10^5
0 <= headID < n
manager.length == n
0 <= manager[i] < n
manager[headID] == -1
informTime.length == n
0 <= informTime[i] <= 1000
informTime[i] == 0 if employee i has no subordinates.
It is guaranteed that all the employees can be informed.

Solution 1: Build the graph + DFS

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {

vector<vector<int>> es(n);

for (int i = 0; i < n; ++i)

if (i != headID) es[manager[i]].push_back(i);

function<int(int)> dfs = [&](int cur) {

int t = 0;

for (int e : es[cur])

t = max(t, dfs(e));

return t + informTime[cur];

};

return dfs(headID);

}

};

Solution 2: Recursion with memoization

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {

vector<int> cache(n, -1);

function<int(int)> dfs = [&](int cur) {

if (cur == -1) return 0;

if (cache[cur] == -1)

cache[cur] = dfs(manager[cur]) + informTime[cur];

return cache[cur];

};

int ans = 0;

for (int i = 0; i < n; ++i)

ans = max(ans, dfs(i));

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def numOfMinutes(self, n: int, headID: int, manager: List[int], informTime: List[int]) -> int:

cache = [-1] * n

def dfs(cur):

if cur == -1: return 0

if cache[cur] == -1:

cache[cur] = dfs(manager[cur]) + informTime[cur]

return cache[cur]

return max([dfs(i) for i in range(n)])

花花酱 LeetCode 1375. Bulb Switcher III

By zxi on March 8, 2020

There is a room with n bulbs, numbered from 1 to n, arranged in a row from left to right. Initially, all the bulbs are turned off.

At moment k (for k from 0 to n - 1), we turn on the light[k] bulb. A bulb change color to blue only if it is on and all the previous bulbs (to the left) are turned on too.

Return the number of moments in which all turned on bulbs are blue.

Example 1:

Input: light = [2,1,3,5,4]
Output: 3
Explanation: All bulbs turned on, are blue at the moment 1, 2 and 4.

Example 2:

Input: light = [3,2,4,1,5]
Output: 2
Explanation: All bulbs turned on, are blue at the moment 3, and 4 (index-0).

Example 3:

Input: light = [4,1,2,3]
Output: 1
Explanation: All bulbs turned on, are blue at the moment 3 (index-0).
Bulb 4th changes to blue at the moment 3.

Example 4:

Input: light = [2,1,4,3,6,5]
Output: 3

Example 5:

Input: light = [1,2,3,4,5,6]
Output: 6

Constraints:

n == light.length
1 <= n <= 5 * 10^4
light is a permutation of [1, 2, ..., n]

Solution

Track the right most light l_k, all turned-on lights are blue if and only if the right most one is k, and there are exact k lights on right now.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int numTimesAllBlue(vector<int>& light) {

int ans = 0;

int right = 0;

for (int i = 0; i < light.size(); ++i) {

right = max(right, light[i]);

ans += right == i + 1;

}

return ans;

}

};

花花酱 LeetCode 1374. Generate a String With Characters That Have Odd Counts

By zxi on March 8, 2020

Given an integer n, return a string with n characters such that each character in such string occurs an odd number of times.

The returned string must contain only lowercase English letters. If there are multiples valid strings, return any of them.

Example 1:

Input: n = 4
Output: "pppz"
Explanation: "pppz" is a valid string since the character 'p' occurs three times and the character 'z' occurs once. Note that there are many other valid strings such as "ohhh" and "love".

Example 2:

Input: n = 2
Output: "xy"
Explanation: "xy" is a valid string since the characters 'x' and 'y' occur once. Note that there are many other valid strings such as "ag" and "ur".

Example 3:

Input: n = 7
Output: "holasss"

Constraints:

1 <= n <= 500

Solution: Greedy

if n is odd, return n ‘a’s.
otherwise, return n -1 ‘a’s and 1 ‘b’

Time complexity: O(n)
Space complexity: O(n) or O(1)

C++

// Author: Huahua

class Solution {

public:

string generateTheString(int n) {

return n & 1 ? string(n, 'a') : string(n - 1, 'a') + "b";

}

};

Python3

# Author: Huahua

class Solution:

def generateTheString(self, n: int) -> str:

ans = ['a'] * n if n % 2 == 1 else ['a'] * (n - 1) + ['b']

return ''.join(ans)

花花酱 LeetCode 1373. Maximum Sum BST in Binary Tree

By zxi on March 8, 2020

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

Constraints:

Each tree has at most 40000 nodes..
Each node’s value is between [-4 * 10^4 , 4 * 10^4].

Solution: Recursion

Time complexity: O(n)
Space complexity: O(h)

C++

// Author: Huahua

class Solution {

public:

int maxSumBST(TreeNode* root) {

int ans = 0;

dfs(root, &ans);

return ans;

}

private:

// returns {lo, hi, sum, valid_bst}

tuple<int, int, int, bool> dfs(TreeNode* root, int* ans) {

if (!root) return {INT_MAX, INT_MIN, 0, true};

auto [ll, lh, ls, lv] = dfs(root->left, ans);

auto [rl, rh, rs, rv] = dfs(root->right, ans);

bool valid = lv && rv && root->val > lh && root->val < rl;

int sum = valid ? ls + rs + root->val : -1;

*ans = max(*ans, sum);

return {min(ll, root->val), max(rh, root->val), sum, valid};

}

};

Python3

# Author: Huahua

class Solution:

def maxSumBST(self, root: TreeNode) -> int:

# returns {lo, hi, sum, valid}

def dfs(node):

if not node: return (1e9, -1e9, 0, True)

ll, lh, ls, lv = dfs(node.left)

rl, rh, rs, rv = dfs(node.right)

v = lv and rv and node.val > lh and node.val < rl

s = ls + rs + node.val if v else -1

self.ans = max(self.ans, s)

return (min(ll, node.val), max(rh, node.val), s, v)

self.ans = 0

dfs(root)

return self.ans