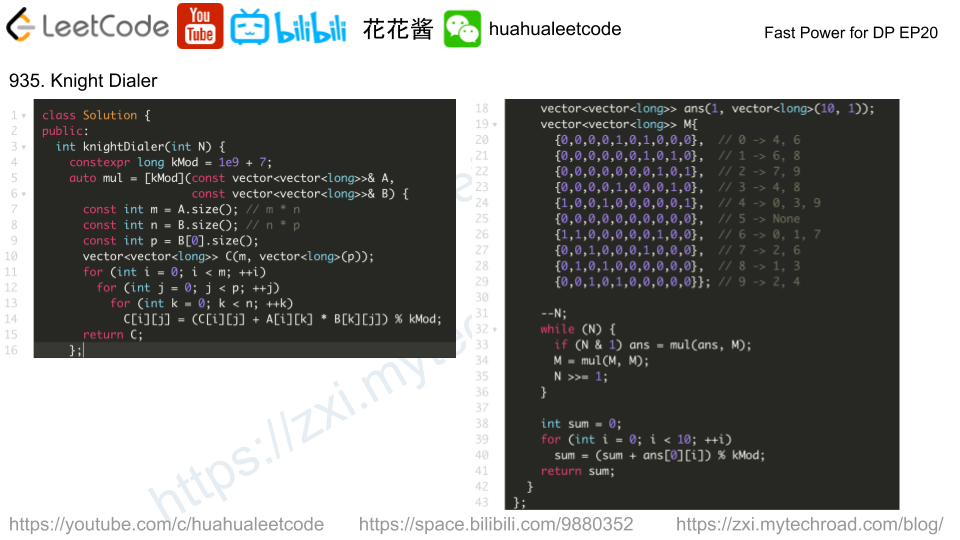
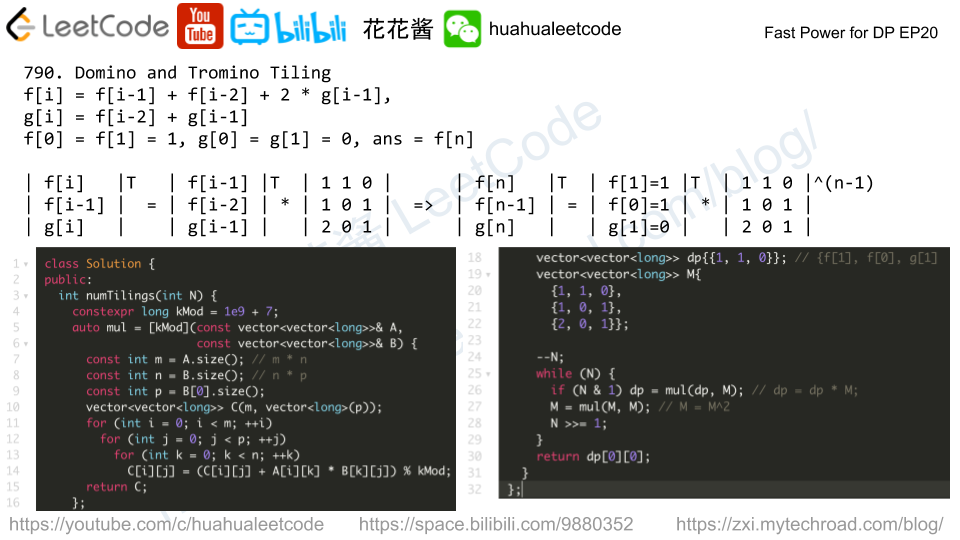
Iterative DP usually takes O(n) to compute dp[n] from dp[0], we could do better if the problem can be written as matrix multiplication. With fast power, dp[n] can be computed in O(logn)
Huahua's Tech Road
You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colours: Red, Yellow or Green while making sure that no two adjacent cells have the same colour (i.e no two cells that share vertical or horizontal sides have the same colour).
You are given n the number of rows of the grid.
Return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 10^9 + 7.
Example 1:
Input: n = 1 Output: 12 Explanation: There are 12 possible way to paint the grid as shown:
Example 2:
Input: n = 2 Output: 54
Example 3:
Input: n = 3 Output: 246
Example 4:
Input: n = 7 Output: 106494
Example 5:
Input: n = 5000 Output: 30228214
Constraints:
n == grid.lengthgrid[i].length == 31 <= n <= 5000
Solution: DP
dp[i][0] := # of ways to paint i rows with 2 different colors at the i-th row
dp[i][1] := # of ways to paint i rows with 3 different colors at the i-th row
dp[1][0] = dp[1][1] = 6
dp[i][0] = dp[i-1][0] * 3 + dp[i-1][1] * 2
dp[i][1] = dp[i-1][0] * 2 + dp[i-1][1] * 2
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// Author: Huahua class Solution { public: int numOfWays(int n) { constexpr int kMod = 1e9 + 7; // dp[i][0] = # of ways to paint i rows with i-th row has 2 colors (e.g. 121) // dp[i][1] = # of ways to paint i rows with i-th row has 3 colors (e.g. 123) // dp[1][0] = dp[1][1] = 6. vector<vector<long>> dp(n + 1, vector<long>(2, 6)); for (int i = 2; i <= n; ++i) { // 121 => 2 colors x 3 {212, 232, 313}, 3 colors x 2 {213, 312} // 123 => 2 colors x 2 {212, 232}, 3 colors x 2 {231, 312} dp[i][0] = (dp[i - 1][0] * 3 + dp[i - 1][1] * 2) % kMod; dp[i][1] = (dp[i - 1][0] * 2 + dp[i - 1][1] * 2) % kMod; } return (dp[n][0] + dp[n][1]) % kMod; } }; |
Python3
|
1 2 3 4 5 6 7 8 9 |
# Author: Huahua class Solution: def numOfWays(self, n: int) -> int: kMod = 10**9 + 7 dp2, dp3 = 6, 6 for i in range(1, n): t2, t3 = dp2 * 3 + dp3 * 2, dp2 * 2 + dp3 * 2 dp2, dp3 = t2 % kMod, t3 % kMod return (dp2 + dp3) % kMod |
Solution 2: DP w/ Matrix Chain Multiplication
ans = {6, 6} * {{3, 2}, {2,2}} ^ (n-1)
Time complexity: O(logn)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
// Author: Huahua class Solution { public: int numOfWays(int n) { constexpr long kMod = 1e9 + 7; vector<vector<long>> ans{{6, 6}}; // 1x2 vector<vector<long>> M{{3, 2},{2,2}}; // 2x2 auto mul = [kMod](const vector<vector<long>>& A, const vector<vector<long>>& B) { const int m = A.size(); // m * n const int n = B.size(); // n * p const int p = B[0].size(); vector<vector<long>> C(m, vector<long>(p)); for (int i = 0; i < m; ++i) for (int j = 0; j < p; ++j) for (int k = 0; k < n; ++k) C[i][j] += (A[i][k] * B[k][j]) % kMod; return C; }; --n; while (n) { if (n & 1) ans = mul(ans, M); // ans = ans * M; M = mul(M, M); // M = M^2 n >>= 1; } // ans = ans0 * M^(n-1) return (ans[0][0] + ans[0][1]) % kMod; } }; |
HTML entity parser is the parser that takes HTML code as input and replace all the entities of the special characters by the characters itself.
The special characters and their entities for HTML are:
- Quotation Mark: the entity is
"and symbol character is". - Single Quote Mark: the entity is
'and symbol character is'. - Ampersand: the entity is
&and symbol character is&. - Greater Than Sign: the entity is
>and symbol character is>. - Less Than Sign: the entity is
<and symbol character is<. - Slash: the entity is
⁄and symbol character is/.
Given the input text string to the HTML parser, you have to implement the entity parser.
Return the text after replacing the entities by the special characters.
Example 1:
Input: text = "& is an HTML entity but &ambassador; is not." Output: "& is an HTML entity but &ambassador; is not." Explanation: The parser will replace the & entity by &
Example 2:
Input: text = "and I quote: "..."" Output: "and I quote: \"...\""
Example 3:
Input: text = "Stay home! Practice on Leetcode :)" Output: "Stay home! Practice on Leetcode :)"
Example 4:
Input: text = "x > y && x < y is always false" Output: "x > y && x < y is always false"
Example 5:
Input: text = "leetcode.com⁄problemset⁄all" Output: "leetcode.com/problemset/all"
Constraints:
1 <= text.length <= 10^5- The string may contain any possible characters out of all the 256 ASCII characters.
Solution: Simulation
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
// Author: Huahua class Solution { public: string entityParser(string text) { map<string, string> m{ {""", "\""}, {"'", "'"}, {"&", "&"}, {">", ">"}, {"<", "<"}, {"⁄", "/"}}; string ans; string buf; for (char c : text) { buf += c; if (buf.back() != ';') continue; const int l = buf.size(); for (const auto& [k, v] : m) { const int kl = k.length(); if (l >= kl && buf.substr(l - kl) == k) { ans += buf.substr(0, l - kl) + v; buf.clear(); break; } } } return ans + buf; } }; |
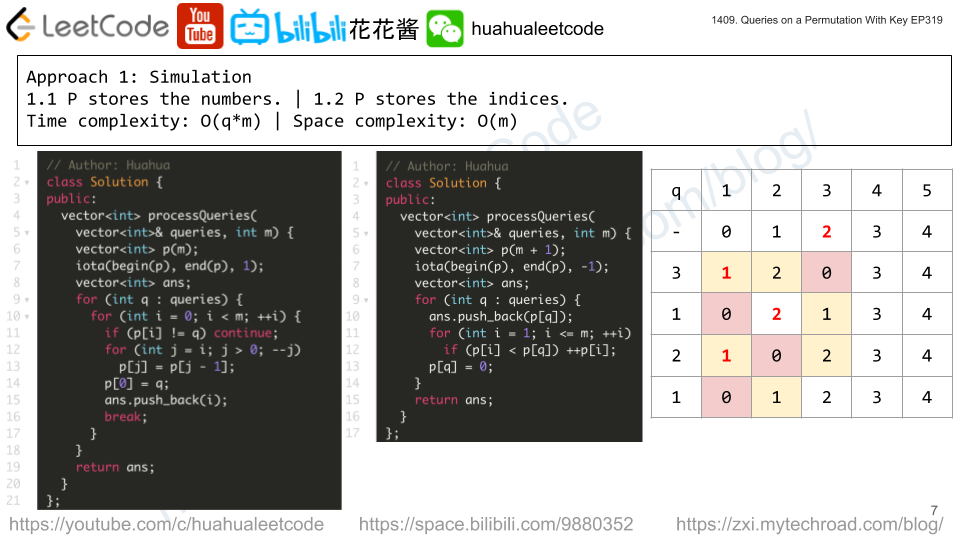
Given the array queries of positive integers between 1 and m, you have to process all queries[i] (from i=0 to i=queries.length-1) according to the following rules:
- In the beginning, you have the permutation
P=[1,2,3,...,m]. - For the current
i, find the position ofqueries[i]in the permutationP(indexing from 0) and then move this at the beginning of the permutationP.Notice that the position ofqueries[i]inPis the result forqueries[i].
Return an array containing the result for the given queries.
Example 1:
Input: queries = [3,1,2,1], m = 5 Output: [2,1,2,1] Explanation: The queries are processed as follow: For i=0: queries[i]=3, P=[1,2,3,4,5], position of 3 in P is 2, then we move 3 to the beginning of P resulting in P=[3,1,2,4,5]. For i=1: queries[i]=1, P=[3,1,2,4,5], position of 1 in P is 1, then we move 1 to the beginning of P resulting in P=[1,3,2,4,5]. For i=2: queries[i]=2, P=[1,3,2,4,5], position of 2 in P is 2, then we move 2 to the beginning of P resulting in P=[2,1,3,4,5]. For i=3: queries[i]=1, P=[2,1,3,4,5], position of 1 in P is 1, then we move 1 to the beginning of P resulting in P=[1,2,3,4,5]. Therefore, the array containing the result is [2,1,2,1].
Example 2:
Input: queries = [4,1,2,2], m = 4 Output: [3,1,2,0]
Example 3:
Input: queries = [7,5,5,8,3], m = 8 Output: [6,5,0,7,5]
Constraints:
1 <= m <= 10^31 <= queries.length <= m1 <= queries[i] <= m
Solution1: Simulation + Hashtable
Use a hashtable to store the location of each key.
For each query q, use h[q] to get the index of q, for each key, if its current index is less than q, increase their indices by 1. (move right). Set h[q] to 0.
Time complexity: O(q*m)
Space complexity: O(m)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class Solution { public: vector<int> processQueries(vector<int>& queries, int m) { vector<int> p(m + 1); iota(begin(p), end(p), -1); vector<int> ans; for (int q : queries) { ans.push_back(p[q]); for (int i = 1; i <= m; ++i) if (p[i] < p[q]) ++p[i]; p[q] = 0; } return ans; } }; |
Solution 2: Fenwick Tree + HashTable
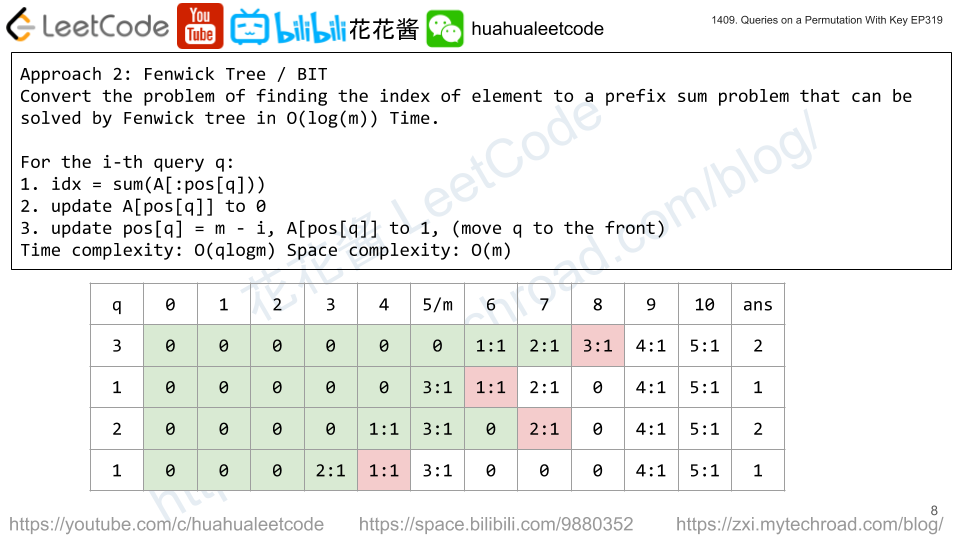
Time complexity: O(qlogm)
Space complexity: O(m)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
// Author: Huahua class Fenwick { public: explicit Fenwick(int n): vals_(n) {} // sum(A[1~i]) int query(int i) const { int s = 0; while (i > 0) { s += vals_[i]; i -= i & -i; } return s; } // A[i] += delta void update(int i, int delta) { while (i < vals_.size()) { vals_[i] += delta; i += i & -i; } } private: vector<int> vals_; }; class Solution { public: vector<int> processQueries(vector<int>& queries, int m) { Fenwick tree(m * 2 + 1); vector<int> pos(m + 1); for (int i = 1; i <= m; ++i) tree.update(pos[i] = i + m, 1); vector<int> ans; for (int q : queries) { ans.push_back(tree.query(pos[q] - 1)); tree.update(pos[q], -1); // set to 0. tree.update(pos[q] = m--, 1); // move to the front. } return ans; } }; |
Python3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
class Fenwick: def __init__(self, n): self.n = n self.val = [0] * n def query(self, i): s = 0 while i > 0: s += self.val[i] i -= i & -i return s def update(self, i, delta): while i < self.n: self.val[i] += delta i += i & -i class Solution: def processQueries(self, queries: List[int], m: int) -> List[int]: pos = [i + m for i in range(m + 1)] tree = Fenwick(2 * m + 1) for i in range(1, m + 1): tree.update(i + m, 1) ans = [] for q in queries: ans.append(tree.query(pos[q] - 1)) tree.update(pos[q], -1) pos[q] = m m -= 1 tree.update(pos[q], 1) return ans |
Given an array of string words. Return all strings in words which is substring of another word in any order.
String words[i] is substring of words[j], if can be obtained removing some characters to left and/or right side of words[j].
Example 1:
Input: words = ["mass","as","hero","superhero"] Output: ["as","hero"] Explanation: "as" is substring of "mass" and "hero" is substring of "superhero". ["hero","as"] is also a valid answer.
Example 2:
Input: words = ["leetcode","et","code"] Output: ["et","code"] Explanation: "et", "code" are substring of "leetcode".
Example 3:
Input: words = ["blue","green","bu"] Output: []
Constraints:
1 <= words.length <= 1001 <= words[i].length <= 30words[i]contains only lowercase English letters.- It’s guaranteed that
words[i]will be unique.
Solution: Brute Force
Time complexity: O(n^2)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
// Author: Huahua class Solution { public: vector<string> stringMatching(vector<string>& words) { vector<string> ans; const int n = words.size(); for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) { if (i == j) continue; if (words[j].find(words[i]) != string::npos) { ans.push_back(words[i]); break; } } return ans; } }; |