Huahua’s Tech Road

花花酱 LeetCode 1373. Maximum Sum BST in Binary Tree

By zxi on March 8, 2020

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:

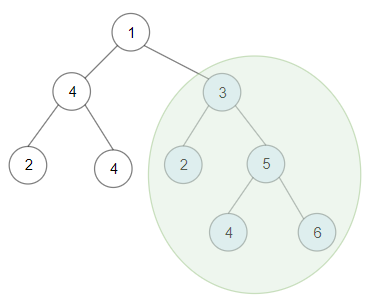
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

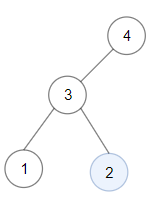
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

Constraints:

Each tree has at most 40000 nodes..
Each node’s value is between [-4 * 10^4 , 4 * 10^4].

Solution: Recursion

Time complexity: O(n)
Space complexity: O(h)

C++

// Author: Huahua

class Solution {

public:

int maxSumBST(TreeNode* root) {

int ans = 0;

dfs(root, &ans);

return ans;

}

private:

// returns {lo, hi, sum, valid_bst}

tuple<int, int, int, bool> dfs(TreeNode* root, int* ans) {

if (!root) return {INT_MAX, INT_MIN, 0, true};

auto [ll, lh, ls, lv] = dfs(root->left, ans);

auto [rl, rh, rs, rv] = dfs(root->right, ans);

bool valid = lv && rv && root->val > lh && root->val < rl;

int sum = valid ? ls + rs + root->val : -1;

*ans = max(*ans, sum);

return {min(ll, root->val), max(rh, root->val), sum, valid};

}

};

Python3

# Author: Huahua

class Solution:

def maxSumBST(self, root: TreeNode) -> int:

# returns {lo, hi, sum, valid}

def dfs(node):

if not node: return (1e9, -1e9, 0, True)

ll, lh, ls, lv = dfs(node.left)

rl, rh, rs, rv = dfs(node.right)

v = lv and rv and node.val > lh and node.val < rl

s = ls + rs + node.val if v else -1

self.ans = max(self.ans, s)

return (min(ll, node.val), max(rh, node.val), s, v)

self.ans = 0

dfs(root)

return self.ans

花花酱 LeetCode 1372. Longest ZigZag Path in a Binary Tree

By zxi on March 8, 2020

Given a binary tree root, a ZigZag path for a binary tree is defined as follow:

Choose any node in the binary tree and a direction (right or left).
If the current direction is right then move to the right child of the current node otherwise move to the left child.
Change the direction from right to left or right to left.
Repeat the second and third step until you can’t move in the tree.

Zigzag length is defined as the number of nodes visited – 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

Example 1:

Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2:

Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3:

Input: root = [1]
Output: 0

Constraints:

Each tree has at most 50000 nodes..
Each node’s value is between [1, 100].

Solution: Recursion

For each node return
1. max ZigZag length if go left
2. max ZigZag length if go right
3. maz ZigZag length within the subtree

ZigZag(root):
ll, lr, lm = ZigZag(root.left)
rl, rr, rm = ZigZag(root.right)
return (lr+1, rl + 1, max(lr+1, rl+1, lm, rm))

Time complexity: O(n)
Space complexity: O(h)

C++

// Author: Huahua

class Solution {

public:

int longestZigZag(TreeNode* root) {

return get<2>(ZigZag(root));

}

// Returns {left, right, max}

tuple<int, int, int> ZigZag(TreeNode* root) {

if (!root) return {-1, -1, -1};

auto [ll, lr, lm] = ZigZag(root->left);

auto [rl, rr, rm] = ZigZag(root->right);

int l = lr + 1;

int r = rl + 1;

return {l, r, max({l, r, lm, rm})};

}

};

Python3

# Author: Huahua

class Solution:

def longestZigZag(self, root: TreeNode) -> int:

def ZigZag(node):

if not node: return (-1, -1, -1)

ll, lr, lm = ZigZag(node.left)

rl, rr, rm = ZigZag(node.right)

return (lr + 1, rl + 1, max(lr + 1, rl + 1, lm, rm))

return ZigZag(root)[2]

花花酱 LeetCode 1371. Find the Longest Substring Containing Vowels in Even Counts

By zxi on March 8, 2020

Given the string s, return the size of the longest substring containing each vowel an even number of times. That is, ‘a’, ‘e’, ‘i’, ‘o’, and ‘u’ must appear an even number of times.

Example 1:

Input: s = "eleetminicoworoep"
Output: 13
Explanation: The longest substring is "leetminicowor" which contains two each of the vowels: e, i and o and zero of the vowels: a and u.

Example 2:

Input: s = "leetcodeisgreat"
Output: 5
Explanation: The longest substring is "leetc" which contains two e's.

Example 3:

Input: s = "bcbcbc"
Output: 6
Explanation: In this case, the given string "bcbcbc" is the longest because all vowels: a, e, i, o and u appear zero times.

Constraints:

1 <= s.length <= 5 x 10^5
s contains only lowercase English letters.

Solution: HashTable

Record the first index when a state occurs. index – last_index is the length of the all-even-vowel substring.

State: {a: odd|even, e: odd|even, …, u:odd|even}.

There are total 2^5 = 32 states that can be represented as a binary string.

whenever a vowel occurs, we flip the bit, e.g. odd->even, even->odd using XOR.

Time complexity: O(5*n)
Space complexity: O(32)

C++

// Author: Huahua

class Solution {

public:

int findTheLongestSubstring(string s) {

const char vowels[] = "aeiou";

vector<int> idx(1 << 5, INT_MAX); // state -> first_index

idx[0] = -1;

int state = 0;

int ans = 0;

for (int i = 0; i < s.length(); ++i) {

for (int j = 0; j < 5; ++j)

if (s[i] == vowels[j]) state ^= 1 << j;

if (idx[state] == INT_MAX) idx[state] = i;

ans = max(ans, i - idx[state]);

}

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def findTheLongestSubstring(self, s: str) -> int:

idx = {0 : -1}

vowels = "aeiou"

state = 0

ans = 0

for i in range(len(s)):

j = vowels.find(s[i])

if j >= 0: state ^= 1 << j

if state not in idx:

idx[state] = i

ans = max(ans, i - idx[state])

return ans

花花酱 LeetCode 1370. Increasing Decreasing String

By zxi on March 7, 2020

Given a string s. You should re-order the string using the following algorithm:

Pick the smallest character from s and append it to the result.
Pick the smallest character from s which is greater than the last appended character to the result and append it.
Repeat step 2 until you cannot pick more characters.
Pick the largest character from s and append it to the result.
Pick the largest character from s which is smaller than the last appended character to the result and append it.
Repeat step 5 until you cannot pick more characters.
Repeat the steps from 1 to 6 until you pick all characters from s.

In each step, If the smallest or the largest character appears more than once you can choose any occurrence and append it to the result.

Return the result string after sorting s with this algorithm.

Example 1:

Input: s = "aaaabbbbcccc"
Output: "abccbaabccba"
Explanation: After steps 1, 2 and 3 of the first iteration, result = "abc"
After steps 4, 5 and 6 of the first iteration, result = "abccba"
First iteration is done. Now s = "aabbcc" and we go back to step 1
After steps 1, 2 and 3 of the second iteration, result = "abccbaabc"
After steps 4, 5 and 6 of the second iteration, result = "abccbaabccba"

Example 2:

Input: s = "rat"
Output: "art"
Explanation: The word "rat" becomes "art" after re-ordering it with the mentioned algorithm.

Example 3:

Input: s = "leetcode"
Output: "cdelotee"

Example 4:

Input: s = "ggggggg"
Output: "ggggggg"

Example 5:

Input: s = "spo"
Output: "ops"

Constraints:

1 <= s.length <= 500
s contains only lower-case English letters.

Solution: Counting frequency of each character

Time complexity: O(n * 26)
Space complexity: O(26)

C++

// Author: Huahua

class Solution {

public:

string sortString(string s) {

vector<int> count(26);

for (char c : s) ++count[c - 'a'];

string ans;

while (ans.length() != s.length()) {

for (char c = 'a'; c <= 'z'; ++c)

if (--count[c - 'a'] >= 0)

ans += c;

for (char c = 'z'; c >= 'a'; --c)

if (--count[c - 'a'] >= 0)

ans += c;

}

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def sortString(self, s: str) -> str:

seq = string.ascii_lowercase + string.ascii_lowercase[::-1]

count = collections.Counter(s)

ans = ""

while len(ans) != len(s):

for c in seq:

if count[c] > 0:

ans += c

count[c] -= 1

return ans

花花酱 LeetCode 1365. How Many Numbers Are Smaller Than the Current Number

By zxi on March 2, 2020

Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j's such that j != i and nums[j] < nums[i].

Return the answer in an array.

Example 1:

Input: nums = [8,1,2,2,3]
Output: [4,0,1,1,3]
Explanation: 
For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). 
For nums[1]=1 does not exist any smaller number than it.
For nums[2]=2 there exist one smaller number than it (1). 
For nums[3]=2 there exist one smaller number than it (1). 
For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).

Example 2:

Input: nums = [6,5,4,8]
Output: [2,1,0,3]

Example 3:

Input: nums = [7,7,7,7]
Output: [0,0,0,0]

Constraints:

2 <= nums.length <= 500
0 <= nums[i] <= 100

Solution 1: Brute Force

Time complexity: O(n^2)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<int> smallerNumbersThanCurrent(vector<int>& nums) {

const int n = nums.size();

vector<int> ans(n);

for (int i = 0; i < n; ++i)

for (int j = 0; j < n; ++j)

if (i != j && nums[j] < nums[i]) ++ans[i];

return ans;

}

};

Solution 2: Sort + Binary Search

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> smallerNumbersThanCurrent(vector<int>& nums) {

const int n = nums.size();

vector<int> s(nums);

sort(begin(s), end(s));

vector<int> ans(n);

for (int i = 0; i < n; ++i)

ans[i] = distance(begin(s), lower_bound(begin(s), end(s), nums[i]));

return ans;

}

};

Solution 3: Cumulative frequency

Time complexity: O(n)
Space complexity: O(101)

C++

// Author: Huahua

class Solution {

public:

vector<int> smallerNumbersThanCurrent(vector<int>& nums) {

vector<int> f(101);

for (int x : nums) ++f[x];

partial_sum(begin(f), end(f), begin(f));

for (int& x : nums)

x = x == 0 ? 0 : f[x - 1];

return nums;

}

};

Huahua's Tech Road

花花酱 LeetCode 1373. Maximum Sum BST in Binary Tree

Solution: Recursion

C++

Python3

花花酱 LeetCode 1372. Longest ZigZag Path in a Binary Tree

Solution: Recursion

C++

Python3

花花酱 LeetCode 1371. Find the Longest Substring Containing Vowels in Even Counts

Solution: HashTable

C++

Python3

花花酱 LeetCode 1370. Increasing Decreasing String

Solution: Counting frequency of each character

C++

Python3

花花酱 LeetCode 1365. How Many Numbers Are Smaller Than the Current Number

Solution 1: Brute Force

C++

Solution 2: Sort + Binary Search

C++

Solution 3: Cumulative frequency

C++