Huahua’s Tech Road

花花酱 LeetCode 838. Push Dominoes

By zxi on May 6, 2019

here are N dominoes in a line, and we place each domino vertically upright.

In the beginning, we simultaneously push some of the dominoes either to the left or to the right.

After each second, each domino that is falling to the left pushes the adjacent domino on the left.

Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.

When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.

For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.

Given a string “S” representing the initial state. S[i] = 'L', if the i-th domino has been pushed to the left; S[i] = 'R', if the i-th domino has been pushed to the right; S[i] = '.', if the i-th domino has not been pushed.

Return a string representing the final state.

Example 1:

Input: ".L.R...LR..L.."
Output: "LL.RR.LLRRLL.."

Example 2:

Input: "RR.L"
Output: "RR.L"
Explanation: The first domino expends no additional force on the second domino.

Note:

0 <= N <= 10^5
String dominoes contains only 'L‘, 'R' and '.'

Solution: Simulation

Simulate the push process, record the steps from L and R for each domino.
steps(L) == steps(R) => “.”
steps(L) < steps(R) => “L”
steps(L) > steps(R) => “R”

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua, running time: 24 ms, 15.2 MB

class Solution {

public:

string pushDominoes(string D) {

const int n = static_cast<int>(D.size());

vector<int> L(n, INT_MAX), R(n, INT_MAX);

for (int i = 0; i < n; ++i)

if (D[i] == 'L') {

L[i] = 0;

for (int j = i - 1; j >= 0 && D[j] == '.'; --j)

L[j] = L[j + 1] + 1;

} else if (D[i] == 'R') {

R[i] = 0;

for (int j = i + 1; j < n && D[j] == '.'; ++j)

R[j] = R[j - 1] + 1;

}

for (int i = 0; i < n; ++i)

if (L[i] < R[i]) D[i] = 'L';

else if (L[i] > R[i]) D[i] = 'R';

return D;

}

};

花花酱 LeetCode Weekly Contest 135 (1037, 1038, 1039, 1040)

By zxi on May 4, 2019

LeetCode 1037. Valid Boomerang

Solution: Math
Time complexity: O(1)
Space complexity: O(1)

C++

class Solution {

public:

bool isBoomerang(vector<vector<int>>& points) {

if (points[0] == points[1] ||

points[1] == points[2] ||

points[0] == points[2]) return false;

int dx0 = points[0][0] - points[1][0];

int dy0 = points[0][1] - points[1][1];

int dx1 = points[0][0] - points[2][0];

int dy1 = points[0][1] - points[2][1];

return dy0 * dx1 != dy1 * dx0;

}

};

LeetCode 1038. Binary Search Tree to Greater Sum Tree

Solution: Recursion: right, root, left

Time complexity: O(n)
Space complexity: O(n)

C++

class Solution {

public:

TreeNode* bstToGst(TreeNode* root) {

int s = 0;

function<void(TreeNode*)> dfs = [&](TreeNode* n) {

if (!n) return;

dfs(n->right);

n->val = s += n->val;

dfs(n->left);

};

dfs(root);

return root;

}

};

1039. Minimum Score Triangulation of Polygon

Solution: DP

Init: dp[i][j] = 0 if 0 <= j – i <= 1
dp[i][j] := min score to triangulate A[i] ~ A[j]
dp[i][j] = min{dp[i][k] + dp[k][j] + A[i]*A[k]*A[j]), i < k < j
answer: dp[0][n – 1]

Time complexity: O(n^3)
Space complexity: O(n^2)

C++/bottom-up

class Solution {

public:

int minScoreTriangulation(vector<int>& A) {

const int n = A.size();

vector<vector<int>> dp(n, vector<int>(n));

for (int l = 3; l <= n; ++l)

for (int i = 0; i + l <= n; ++i) {

int j = i + l - 1;

dp[i][j] = INT_MAX;

for (int k = i + 1; k <= j - 1; ++k)

dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + A[i] * A[k] * A[j]);

}

return dp[0][n - 1];

}

};

C++/top-down

class Solution {

public:

int minScoreTriangulation(vector<int>& A) {

const int n = A.size();

vector<vector<int>> dp(n, vector<int>(n, INT_MAX));

function<int(int, int)> solve = [&](int i, int j) {

if (j - i <= 1) return 0;

if (dp[i][j] != INT_MAX) return dp[i][j];

dp[i][j] = INT_MAX;

for (int k = i + 1; k <= j - 1; ++k)

dp[i][j] = min(dp[i][j],

solve(i, k) + solve(k, j) + A[i] * A[k] * A[j]);

return dp[i][j];

};

return solve(0, n - 1);

}

};

Python

"Author: Huahua"

from functools import lru_cache

class Solution:

def minScoreTriangulation(self, A: List[int]) -> int:

@lru_cache(None)

def dp(i, j):

return 0 if j - i <= 1 else min(dp(i, k) + dp(k, j) + A[i] * A[k] * A[j] for k in range(i + 1, j))

return dp(0, len(A) - 1)

1040. Moving Stones Until Consecutive II

Solution: Sliding Window

Time complexity: O(nlogn)
Space complexity: O(1)

C++

class Solution {

public:

vector<int> numMovesStonesII(vector<int>& stones) {

const int n = static_cast<int>(stones.size());

sort(begin(stones), end(stones));

int max_steps = max(stones[n - 1] - stones[1] - n + 2,

stones[n - 2] - stones[0] - n + 2);

int min_steps = INT_MAX;

int i = 0;

for (int j = 0; j < n; ++j) {

while (stones[j] - stones[i] >= n) ++i;

if (j - i + 1 == n - 1 && stones[j] - stones[i] == n - 2)

min_steps = min(min_steps, 2);

else

min_steps = min(min_steps, n - (j - i + 1));

}

return {min_steps, max_steps};

}

};

花花酱 LeetCode 851. Loud and Rich

By zxi on May 4, 2019

In a group of N people (labelled 0, 1, 2, ..., N-1), each person has different amounts of money, and different levels of quietness.

For convenience, we’ll call the person with label x, simply “person x“.

We’ll say that richer[i] = [x, y] if person x definitely has more money than person y. Note that richer may only be a subset of valid observations.

Also, we’ll say quiet[x] = q if person x has quietness q.

Now, return answer, where answer[x] = y if y is the least quiet person (that is, the person y with the smallest value of quiet[y]), among all people who definitely have equal to or more money than person x.

Example 1:

Input: richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
Output: [5,5,2,5,4,5,6,7]
Explanation: 
answer[0] = 5.
Person 5 has more money than 3, which has more money than 1, which has more money than 0.
The only person who is quieter (has lower quiet[x]) is person 7, but
it isn't clear if they have more money than person 0.

answer[7] = 7.
Among all people that definitely have equal to or more money than person 7
(which could be persons 3, 4, 5, 6, or 7), the person who is the quietest (has lower quiet[x])
is person 7.

The other answers can be filled out with similar reasoning.

Note:

1 <= quiet.length = N <= 500
0 <= quiet[i] < N, all quiet[i] are different.
0 <= richer.length <= N * (N-1) / 2
0 <= richer[i][j] < N
richer[i][0] != richer[i][1]
richer[i]‘s are all different.
The observations in richer are all logically consistent.

Solution: DFS + Memoization

For person i , remember the quietest person who is richer than person i.

Time complexity: O(n^2)
Space complexity: O(n)

C++

// Author: Huahua, running time: 108 ms, 31.6 MB

class Solution {

public:

vector<int> loudAndRich(vector<vector<int>>& richer, vector<int>& quiet) {

const int n = quiet.size();

vector<vector<int>> g(n);

for (const auto& r : richer)

g[r[1]].push_back(r[0]);

vector<int> ans(n, -1);

function<void(int)> dfs = [&](int i) {

if (ans[i] != -1) return;

ans[i] = i;

for (int j : g[i]) {

dfs(j);

if (quiet[ans[j]] < quiet[ans[i]])

ans[i] = ans[j];

}

};

for (int i = 0; i < n; ++i) dfs(i);

return ans;

}

};

花花酱 8 Puzzles – Bidirectional A* vs Bidirectional BFS

By zxi on April 30, 2019

8 Puzzles # nodes expended of 1000 solvable instances

Conclusion:

Nodes expended: BiDirectional A* << A* (Manhattan) <= Bidirectional BFS < A* Hamming << BFS
Running time: BiDirectional A* < Bidirectional BFS <= A* (Manhattan) < A* Hamming << BFS

Code:

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

# Author: Huahua

from collections import deque

import heapq

import numpy as np

import random

import sys

N = 3

def Manhattan(s1, s2):

dist = 0

for i1, d in enumerate(s1):

i2 = s2.index(d)

x1 = i1 % N

y1 = i1 // N

x2 = i2 % N

y2 = i2 // N

dist += abs(x1 - x2) + abs(y1 - y2)

return dist

def Hamming(s1, s2):

return sum(x != y for x, y in zip(s1, s2))

class Node:

dirs = [0, -1, 0, 1, 0]

def __init__(self, state, parent = None, h = 0):

self.state = state

self.parent = parent

self.g = parent.g + 1 if parent else 0

self.h = h

self.f = self.g + self.h

def getMoves(self):

moves = []

index = self.state.index(0)

x = index % N

y = index // N

for i in range(4):

tx = x + Node.dirs[i]

ty = y + Node.dirs[i + 1]

if tx < 0 or ty < 0 or tx == N or ty == N:

continue

i = ty * N + tx

move = list(self.state)

move[index] = move[i]

move[i] = 0

moves.append(tuple(move))

return moves

def print(self):

print(np.reshape(self.state, (N, N)))

def __lt__(self, other):

return self.f < other.f

def AStarSearch(start_state, end_state, heuristic):

def h(s):

return heuristic(s, end_state)

q = []

s = Node(start_state, h=h(start_state))

heapq.heappush(q, s)

opened = {s.state : s.f}

closed = dict()

while q:

n = heapq.heappop(q)

if n.state == end_state:

return n, len(opened), len(closed)

if n.state in closed: continue

closed[n.state] = n.f

for move in n.getMoves():

node = Node(move, n, h(move))

if move in opened and opened[move] <= node.f: continue

opened[node.state] = node.f

heapq.heappush(q, node)

return None, len(opened), len(closed)

def BFS(start_state, end_state):

q = deque()

q.append(Node(start_state))

opened = set(start_state)

closed = 0

while q:

n = q.popleft()

if n.state == end_state:

return n, len(opened), closed

closed += 1

for move in n.getMoves():

if move in opened: continue

opened.add(move)

q.append(Node(move, n))

return None, len(opened), closed

def getRootNode(n):

return getRootNode(n.parent) if n.parent else n

def BidirectionalBFS(start_state, end_state):

def constructPath(p, o):

while o:

t = o.parent

o.parent = p

p, o = o, t

return p

ns = Node(start_state)

ne = Node(end_state)

q = [deque([ns]), deque([ne])]

opened = [{start_state : ns}, {end_state: ne}]

closed = [0, 0]

while q[0]:

l = len(q[0])

while l > 0:

p = q[0].popleft()

closed[0] += 1

for move in p.getMoves():

n = Node(move, p)

if move in opened[1]:

o = opened[1][move]

if getRootNode(n).state == end_state:

o, n = n, o

n = constructPath(n, o.parent)

return n, len(opened[0]) + len(opened[1]), closed[0] + closed[1]

if move in opened[0]: continue

opened[0][move] = n

q[0].append(n)

l -= 1

q.reverse()

opened.reverse()

closed.reverse()

return None, len(opened[0]) + len(opened[1]), closed[0] + closed[1]

def print_path(n):

if not n: return

print_path(n.parent)

n.print()

def solvable(state):

inv = 0

for i in range(N*N):

for j in range(i + 1, N*N):

if all((state[i] > 0, state[j] > 0, state[i] > state[j])):

inv += 1

return inv % 2 == 0

if __name__ == '__main__':

s = [1, 2, 3, 4, 5, 6, 7, 8, 0]

e = [1, 2, 3, 4, 5, 6, 7, 8, 0]

i = 0

while True:

random.shuffle(s)

if not solvable(s): continue

n1, opened1, closed1 = AStarSearch(tuple(s), tuple(e), heuristic=Manhattan)

n2, opened2, closed2 = AStarSearch(tuple(s), tuple(e), heuristic=Hamming)

n3, opened3, closed3 = BFS(tuple(s), tuple(e))

n4, opened4, closed4 = BidirectionalBFS(tuple(s), tuple(e))

print("%d\t%d\t%d\t%d" % (closed1, closed2, closed3, closed4))

sys.stdout.flush()

# print("A*")

# print_path(n1)

# print('---------------')

# print("BFS")

# print_path(n3)

# print('---------------')

# print("Bi-BFS")

# print_path(n4)

# print('---------------')

i += 1

if i == 1000: break

C++ Version

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

296

297

298

299

300

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

318

319

320

321

322

323

324

325

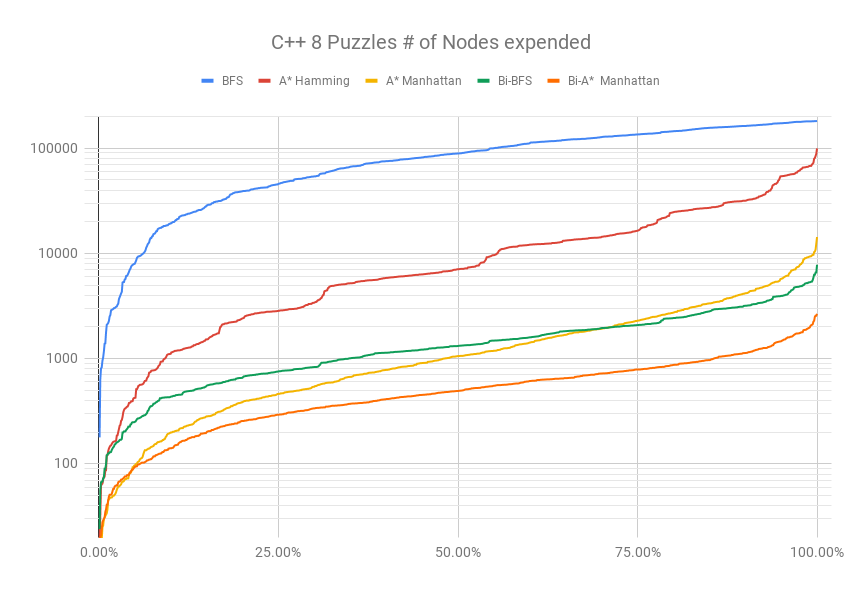
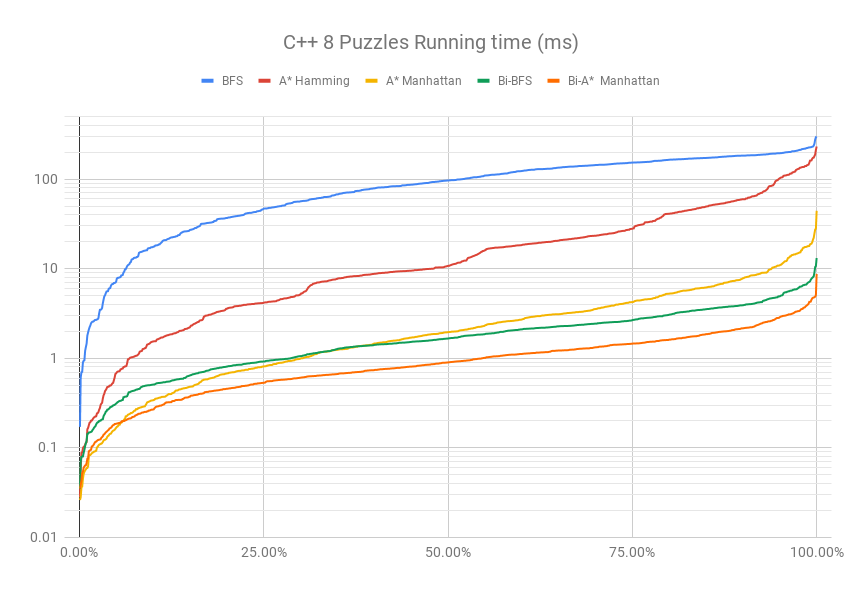
#include <algorithm>

#include <array>

#include <chrono>

#include <deque>

#include <functional>

#include <iostream>

#include <memory>

#include <queue>

#include <unordered_map>

#include <unordered_set>

#include <vector>

using namespace std;

using chrono::high_resolution_clock;

constexpr int N = 3;

constexpr int dirs[] = {0, 1, 0, -1, 0};

struct Node;

typedef string State;

typedef shared_ptr<Node> NodePtr;

typedef function<int(const State& s, const State& t)> Heuristic;

struct Node {

Node(State s, NodePtr p = nullptr, int h = 0)

: s(s), p(p), h(h), g(p ? p->g + 1 : 0), f(this->h + g) {}

vector<State> GetNextStates() const {

vector<State> states;

int index = find(s.begin(), s.end(), '0') - s.begin();

int x = index % N;

int y = index / N;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || ty < 0 || tx == N || ty == N) continue;

int new_index = ty * N + tx;

State next(s);

next[index] = s[new_index];

next[new_index] = '0';

states.push_back(move(next));

}

return states;

}

NodePtr p;

int h;

int g;

int f;

State s;

};

bool Sovlable(const State& s) {

int inv_count = 0;

for (int i = 0; i < N * N; ++i) {

for (int j = i + 1; j < N * N; ++j) {

if (s[i] != '0' && s[j] != '0' && s[i] > s[j]) {

++inv_count;

}

return inv_count % 2 == 0;

}

NodePtr GetRoot(NodePtr n) { return n->p ? GetRoot(n->p) : n; }

NodePtr WirePath(NodePtr p, NodePtr n) {

while (n) {

NodePtr t = n->p;

n->p = p;

p = n;

n = t;

}

return p;

}

void ConstructPath(NodePtr node, vector<State>* path) {

while (node) {

path->push_back(node->s);

node = node->p;

}

reverse(path->begin(), path->end());

}

class Solver {

public:

virtual bool Solve(State start, State target, vector<State>* path,

int* opened, int* closed) = 0;

};

class BFSSolver : public Solver {

public:

bool Solve(State start, State target, vector<State>* path, int* opened,

int* closed) override {

int expended = 0;

unordered_set<string> seen;

deque<NodePtr> q{make_shared<Node>(start)};

while (!q.empty()) {

auto cur = q.front();

q.pop_front();

++expended;

if (cur->s == target) {

ConstructPath(cur, path);

*opened = seen.size();

*closed = expended;

return true;

}

for (const auto& s : cur->GetNextStates()) {

auto r = seen.insert(s);

if (!r.second) continue;

q.push_back(make_shared<Node>(s, cur));

}

return false;

}

};

class BidirectionalBFSSolver : public Solver {

public:

bool Solve(State start, State target, vector<State>* path, int* opened,

int* closed) override {

auto start_node = make_shared<Node>(start);

auto target_node = make_shared<Node>(target);

unordered_map<string, NodePtr> seen0{{start, start_node}};

unordered_map<string, NodePtr> seen1{{target, target_node}};

deque<NodePtr> q0{start_node};

deque<NodePtr> q1{target_node};

int expended = 0;

while (!q0.empty()) {

size_t size = q0.size();

while (size--) {

auto cur = q0.front();

q0.pop_front();

++expended;

for (const auto& s : cur->GetNextStates()) {

auto n = make_shared<Node>(s, cur);

auto it = seen1.find(s);

if (it != seen1.end()) {

auto p = it->second;

if (GetRoot(n)->s == target) swap(n, p);

n = WirePath(n, p->p);

ConstructPath(n, path);

*opened = seen0.size() + seen1.size();

*closed = expended;

return true;

}

if (seen0.count(s)) continue;

seen0[s] = n;

q0.push_back(n);

}

if (q1.size() < q0.size()) {

swap(q0, q1);

swap(seen0, seen1);

}

return false;

}

private:

};

struct NodeCompare : public binary_function<NodePtr, NodePtr, bool> {

bool operator()(const NodePtr& x, const NodePtr& y) const {

return x->f > y->f;

}

};

int ManhattanDistance(const State& s, const State& t) {

int h = 0;

for (int i1 = 0; i1 < N * N; ++i1) {

int i2 = t.find(s[i1]);

int x1 = i1 % N;

int y1 = i1 / N;

int x2 = i2 % N;

int y2 = i2 / N;

h += abs(x1 - x2) + abs(y1 - y2);

}

return h;

}

int HammingDistance(const State& s, const State& t) {

int h = 0;

for (size_t i = 0; i < s.size(); ++i) {

if (s[i] != t[i]) ++h;

}

return h;

}

class AStarSolver : public Solver {

public:

explicit AStarSolver(Heuristic heuristic) : heuristic_(heuristic) {}

bool Solve(State start, State target, vector<State>* path, int* opened,

int* closed) override {

unordered_map<string, NodePtr> o;

unordered_set<string> c;

priority_queue<NodePtr, vector<NodePtr>, NodeCompare> q;

q.emplace(new Node(start, nullptr, heuristic_(start, target)));

while (!q.empty()) {

auto cur = q.top();

q.pop();

if (cur->s == target) {

ConstructPath(cur, path);

*opened = o.size();

*closed = c.size();

return true;

}

if (!c.insert(cur->s).second) continue;

for (const auto& s : cur->GetNextStates()) {

auto it = o.find(s);

auto n = make_shared<Node>(s, cur, heuristic_(s, target));

if (it != o.end() && n->f >= it->second->f) continue;

o[s] = n;

q.push(n);

}

return false;

}

private:

Heuristic heuristic_;

};

class BiAStarSolver : public Solver {

public:

explicit BiAStarSolver(Heuristic heuristic) : heuristic_(heuristic) {}

bool Solve(State start, State target, vector<State>* path, int* opened,

int* closed) override {

unordered_map<string, NodePtr> o0, o1;

unordered_map<string, NodePtr> c0, c1;

priority_queue<NodePtr, vector<NodePtr>, NodeCompare> q0, q1;

q0.emplace(new Node(start, nullptr, heuristic_(start, target)));

q1.emplace(new Node(target, nullptr, heuristic_(target, start)));

bool farward = true;

while (!q0.empty()) {

auto size = q0.size();

while (size--) {

auto cur = q0.top();

q0.pop();

if (c0.count(cur->s)) continue;

c0[cur->s] = cur;

if (c1.count(cur->s)) {

auto p = c1[cur->s];

if (GetRoot(cur)->s == target) swap(cur, p);

cur = WirePath(cur, p->p);

ConstructPath(cur, path);

*opened = o0.size() + o1.size();

*closed = c0.size() + c1.size();

return true;

}

for (const auto& s : cur->GetNextStates()) {

auto it = o0.find(s);

auto n = make_shared<Node>(s, cur,

heuristic_(s, farward ? target : start));

if (it != o0.end() && n->f >= it->second->f) continue;

o0[s] = n;

q0.push(n);

}

if (q1.size() < q0.size()) {

swap(q0, q1);

swap(c0, c1);

swap(o0, o1);

farward = !farward;

}

return false;

}

private:

Heuristic heuristic_;

};

bool VerifyPath(const vector<State>& path, const State& s, const State& t) {

if (path.empty()) return false;

if (path.front() != s || path.back() != t) return false;

for (size_t i = 1; i < path.size(); ++i) {

Node n(path[i - 1]);

auto states = n.GetNextStates();

if (find(begin(states), end(states), path[i]) == end(states)) {

return false;

}

return true;

}

void StatisticsMode() {

State s{"123456780"};

State t{"123456780"};

vector<unique_ptr<Solver>> solvers;

solvers.emplace_back(new BFSSolver);

solvers.emplace_back(new AStarSolver(HammingDistance));

solvers.emplace_back(new AStarSolver(ManhattanDistance));

solvers.emplace_back(new BidirectionalBFSSolver);

solvers.emplace_back(new BiAStarSolver(ManhattanDistance));

for (int i = 0; i < 1000;) {

random_shuffle(s.begin(), s.end());

if (!Sovlable(s)) continue;

++i;

for (auto& solver : solvers) {

vector<State> path;

int opened;

int closed;

auto t0 = high_resolution_clock::now();

bool sovlable = solver->Solve(s, t, &path, &opened, &closed);

auto t1 = high_resolution_clock::now();

if (!VerifyPath(path, s, t)) {

cerr << "Invalid path!" << endl;

return;

}

auto time_span = chrono::duration_cast<chrono::duration<double>>(t1 - t0);

cout << closed << "\t" << time_span.count() * 1000 << "\t";

}

cout << endl;

}

int main() { StatisticsMode(); }

花花酱 LeetCode 853. Car Fleet

By zxi on April 28, 2019

N cars are going to the same destination along a one lane road. The destination is target miles away.

Each car i has a constant speed speed[i] (in miles per hour), and initial position position[i] miles towards the target along the road.

A car can never pass another car ahead of it, but it can catch up to it, and drive bumper to bumper at the same speed.

The distance between these two cars is ignored – they are assumed to have the same position.

A car fleet is some non-empty set of cars driving at the same position and same speed. Note that a single car is also a car fleet.

If a car catches up to a car fleet right at the destination point, it will still be considered as one car fleet.

How many car fleets will arrive at the destination?

Example 1:

Input: target = 12, position = [10,8,0,5,3], speed = [2,4,1,1,3]
Output: 3
Explanation:
The cars starting at 10 and 8 become a fleet, meeting each other at 12.
The car starting at 0 doesn't catch up to any other car, so it is a fleet by itself.
The cars starting at 5 and 3 become a fleet, meeting each other at 6.
Note that no other cars meet these fleets before the destination, so the answer is 3.

Note:

0 <= N <= 10 ^ 4
0 < target <= 10 ^ 6
0 < speed[i] <= 10 ^ 6
0 <= position[i] < target
All initial positions are different.

Solution: Greedy

Compute the time when each car can reach target.
Sort cars by position DESC

Answer will be number slow cars in the time array.

Ex 1: 
target = 12
p = [10,8,0,5,3] 
v = [2,4,1,1,3]


p     t
10    1  <- slow -- ^
 8    1             |
 5    7  <- slow -- ^
 3    3             |
 0   12  <- slow -- ^

Ex 2
target = 10
p = [5, 4, 3, 2, 1]
v = [1, 2, 3, 4, 5]

p     t
5     5  <- slow -- ^
4     3             |
3     2.33          |
2     2             |
1     1.8           |

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua, running time: 52 ms / 10.9 MB

class Solution {

public:

int carFleet(int target, vector<int>& position, vector<int>& speed) {

vector<pair<int, float>> cars(position.size());

for (int i = 0; i < position.size(); ++i)

cars[i] = {position[i], static_cast<float>(target - position[i]) / speed[i]};

sort(rbegin(cars), rend(cars));

int ans{0};

float max_t{0};

for (const auto& [p, t] : cars)

if (t > max_t) {

max_t = t;

++ans;

}

return ans;

}

};

Python3

class Solution:

def carFleet(self, target: int, position: List[int], speed: List[int]) -> int:

cars = sorted([(p, (target - p) / s) for p, s in zip(position, speed)],

key=lambda x: -x[0])

ans, max_t = 0, 0

for p, t in cars:

if t > max_t:

ans += 1

max_t = t

return ans

Huahua's Tech Road

花花酱 LeetCode 838. Push Dominoes

C++

花花酱 LeetCode Weekly Contest 135 (1037, 1038, 1039, 1040)

LeetCode 1037. Valid Boomerang

C++

LeetCode 1038. Binary Search Tree to Greater Sum Tree

C++

1039. Minimum Score Triangulation of Polygon

C++/bottom-up

C++/top-down

Python

1040. Moving Stones Until Consecutive II

C++

花花酱 LeetCode 851. Loud and Rich

C++

花花酱 8 Puzzles – Bidirectional A* vs Bidirectional BFS

花花酱 LeetCode 853. Car Fleet

Solution: Greedy

C++

Python3