花花酱 LeetCode 873. Length of Longest Fibonacci Subsequence

By zxi on July 22, 2018

Problem

A sequence X_1, X_2, ..., X_n is fibonacci-like if:

n >= 3
X_i + X_{i+1} = X_{i+2} for all i + 2 <= n

Given a strictly increasing array A of positive integers forming a sequence, find the length of the longest fibonacci-like subsequence of A. If one does not exist, return 0.

(Recall that a subsequence is derived from another sequence A by deleting any number of elements (including none) from A, without changing the order of the remaining elements. For example, [3, 5, 8] is a subsequence of [3, 4, 5, 6, 7, 8].)

Example 1:

Input: [1,2,3,4,5,6,7,8]
Output: 5
Explanation:
The longest subsequence that is fibonacci-like: [1,2,3,5,8].

Example 2:

Input: [1,3,7,11,12,14,18]
Output: 3
Explanation:
The longest subsequence that is fibonacci-like:
[1,11,12], [3,11,14] or [7,11,18].

Note:

3 <= A.length <= 1000
1 <= A[0] < A[1] < ... < A[A.length - 1] <= 10^9
(The time limit has been reduced by 50% for submissions in Java, C, and C++.)

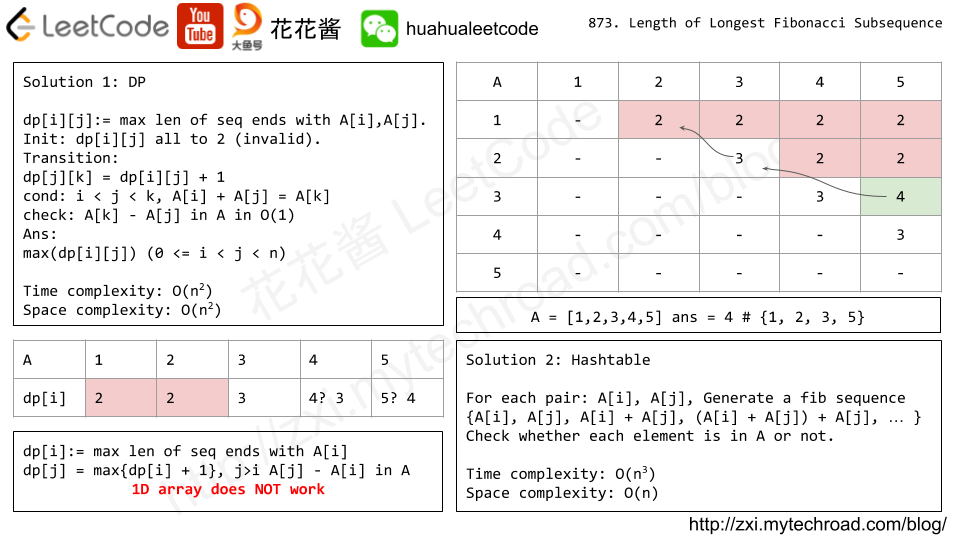
Solution 1: DP

C++

// Author: Huahua

// Running time: 68 ms

// w/ Hashtable

// Time complexity: O(n^2)

// Space complexity: O(n^2)

class Solution {

public:

int lenLongestFibSubseq(vector<int>& A) {

const int n = A.size();

unordered_map<int, int> m;

for (int i = 0; i < n; ++i)

m[A[i]] = i;

vector<vector<int>> dp(n, vector<int>(n, 2));

int ans = 0;

for (int j = 0; j < n; ++j)

for (int k = j + 1; k < n; ++k) {

int a_i = A[k] - A[j];

if (a_i >= A[j]) break; // pruning 168 ms -> 68 ms

auto it = m.find(a_i);

if (it == end(m)) continue;

int i = it->second;

dp[j][k] = dp[i][j] + 1;

ans = max(ans, dp[j][k]);

}

return ans;

}

};

C++ V2

// Author: Huahua

// Running time: 96 ms

// w / Binary Search

// Time complexity: O(n^2logn)

// Space complexity: O(n)

class Solution {

public:

int lenLongestFibSubseq(vector<int>& A) {

const int n = A.size();

vector<vector<int>> dp(n, vector<int>(n, 2));

int ans = 0;

for (int j = 0; j < n; ++j)

for (int k = j + 1; k < n; ++k) {

int a_i = A[k] - A[j];

if (a_i >= A[j]) break;

auto it = lower_bound(begin(A), begin(A) + j, a_i);

int i = it - begin(A);

if (A[i] != a_i) continue;

dp[j][k] = dp[i][j] + 1;

ans = max(ans, dp[j][k]);

}

return ans;

}

};

Solution 2: HashTable

Time complexity: O(n^3)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 172 ms

class Solution {

public:

int lenLongestFibSubseq(vector<int>& A) {

const int n = A.size();

unordered_set<int> m(begin(A), end(A));

int ans = 0;

for (int i = 0; i < n; ++i)

for (int j = i + 1; j < n; ++j) {

int a = A[i];

int b = A[j];

int c = a + b;

int l = 2;

while (m.count(c)) {

a = b;

b = c;

c = a + b;

ans = max(ans, ++l);

}

return ans;

}

};

花花酱 LeetCode 872. Leaf-Similar Trees

By zxi on July 21, 2018

Problem

Consider all the leaves of a binary tree. From left to right order, the values of those leaves form a leaf value sequence.

For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Note:

Both of the given trees will have between 1 and 100 nodes.

Solution: Recursion

Time complexity: O(n1 + n2)

Space complexity: O(n1 + n2)

// Author: Huahua

// Running time: 0 ms

class Solution {

public:

bool leafSimilar(TreeNode* root1, TreeNode* root2) {

vector<int> leafs1;

vector<int> leafs2;

getLeafs(root1, leafs1);

getLeafs(root2, leafs2);

return leafs1 == leafs2;

}

private:

void getLeafs(TreeNode* root, vector<int>& leafs) {

if (root == nullptr) return;

if (root->left == nullptr && root->right == nullptr)

leafs.push_back(root->val);

getLeafs(root->left, leafs);

getLeafs(root->right, leafs);

}

};

Python

"""

Author: Huahua

Running time: 24 ms

"""

class Solution(object):

def leafSimilar(self, root1, root2):

def getLeafs(root):

if not root: return []

if not root.left and not root.right: return [root.val]

return getLeafs(root.left) + getLeafs(root.right)

return getLeafs(root1) == getLeafs(root2)

花花酱 LeetCode 712. Minimum ASCII Delete Sum for Two Strings

By zxi on July 20, 2018

Problem

Given two strings s1, s2, find the lowest ASCII sum of deleted characters to make two strings equal.

Example 1:

Input: s1 = "sea", s2 = "eat"
Output: 231
Explanation: Deleting "s" from "sea" adds the ASCII value of "s" (115) to the sum.
Deleting "t" from "eat" adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.

Example 2:

Input: s1 = "delete", s2 = "leet"
Output: 403
Explanation: Deleting "dee" from "delete" to turn the string into "let",
adds 100[d]+101[e]+101[e] to the sum.  Deleting "e" from "leet" adds 101[e] to the sum.
At the end, both strings are equal to "let", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee" or "eet", we would get answers of 433 or 417, which are higher.

Note:

0 < s1.length, s2.length <= 1000.
All elements of each string will have an ASCII value in [97, 122].

Solution: DP

Time complexity: O(l1 * l2)

Space complexity: O(l1 * l2)

C++

// Author: Huahua

// Running time: 8 ms

class Solution {

public:

int minimumDeleteSum(string s1, string s2) {

const int l1 = s1.length();

const int l2 = s2.length();

// dp[i][j] := min delete sum of (s1.substr(0, i), s2.substr(0, j))

vector<vector<int>> dp(l1 + 1, vector<int>(l2 + 1));

for (int i = 1; i <= l1; ++i)

dp[i][0] = dp[i - 1][0] + s1[i - 1];

for (int j = 1; j <= l2; ++j)

dp[0][j] = dp[0][j - 1] + s2[j - 1];

for (int i = 1; i <= l1; ++i)

for (int j = 1; j <= l2; ++j)

if (s1[i - 1] == s2[j - 1])

// keep s1[i - 1] and s2[j - 1]

dp[i][j] = dp[i - 1][j - 1];

else

dp[i][j] = min(dp[i - 1][j] + s1[i - 1], // delete s1[i - 1]

dp[i][j - 1] + s2[j - 1]); // delete s2[j - 1]

return dp[l1][l2];

}

};

Solution2: Recursion + Memorization

Time complexity: O(l1 * l2)

Space complexity: O(l1 * l2)

C++

// Author: Huahua

// Running time: 20 ms

class Solution {

public:

int minimumDeleteSum(string s1, string s2) {

const int l1 = s1.length();

const int l2 = s2.length();

m_ = vector<vector<int>>(l1 + 1, vector<int>(l2 + 1, INT_MAX));

return dp(s1, l1, s2, l2);

}

private:

int dp(const string& s1, int i, const string& s2, int j) {

if (i == 0 && j == 0) return 0;

if (m_[i][j] != INT_MAX) return m_[i][j];

if (i == 0) // s1 is empty.

return m_[i][j] = dp(s1, i, s2, j - 1) + s2[j - 1];

if (j == 0) // s2 is empty

return m_[i][j] = dp(s1, i - 1, s2, j) + s1[i - 1];

if (s1[i - 1] == s2[j - 1]) // skip s1[i-1] / s2[j-1]

return m_[i][j] = dp(s1, i - 1, s2, j - 1);

return m_[i][j] = min(dp(s1, i - 1, s2, j) + s1[i - 1], // del s1[i-1]

dp(s1, i, s2, j - 1) + s2[j - 1]); // del s2[j-1]

}

vector<vector<int>> m_;

};

Problem

Given a string S and a string T, count the number of distinct subsequences of S which equals T.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).

Example 1:

Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:  As shown below, there are 3 ways you can generate "rabbit" from S. (The caret symbol ^ means the chosen letters) 
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

Example 2:

Input: S = "babgbag", T = "bag"
Output: 5
Explanation:  As shown below, there are 5 ways you can generate "bag" from S. (The caret symbol ^ means the chosen letters)
babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^

Solution: DP

Time complexity: O(|s| * |t|)

Space complexity: O(|s| * |t|)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numDistinct(string s, string t) {

int ls = s.length();

int lt = t.length();

vector<vector<int>> dp(lt + 1, vector<int>(ls + 1));

fill(begin(dp[0]), end(dp[0]), 1);

for (int i = 1; i <= lt; ++i)

for (int j = 1; j <= ls; ++j)

dp[i][j] = dp[i][j - 1] + (t[i - 1] == s[j - 1] ? dp[i - 1][j - 1] : 0);

return dp[lt][ls];

}

};

Problem

A rectangle is represented as a list [x1, y1, x2, y2], where (x1, y1) are the coordinates of its bottom-left corner, and (x2, y2) are the coordinates of its top-right corner.

Two rectangles overlap if the area of their intersection is positive. To be clear, two rectangles that only touch at the corner or edges do not overlap.

Given two (axis-aligned) rectangles, return whether they overlap.

Example 1:

Input: rec1 = [0,0,2,2], rec2 = [1,1,3,3]
Output: true

Example 2:

Input: rec1 = [0,0,1,1], rec2 = [1,0,2,1]
Output: false

Notes:

Both rectangles rec1 and rec2 are lists of 4 integers.
All coordinates in rectangles will be between -10^9 and 10^9.

Solution: Geometry

Time complexity: O(1)

Space complexity: O(1)

// Author: Huahua

// Running time: 0 ms

class Solution {

public:

bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2) {

return rec1[0] < rec2[2] && rec2[0] < rec1[2] &&

rec1[1] < rec2[3] && rec2[1] < rec1[3];

}

};

花花酱 LeetCode 873. Length of Longest Fibonacci Subsequence

Problem

Solution 1: DP

C++

C++ V2

Solution 2: HashTable

C++

花花酱 LeetCode 872. Leaf-Similar Trees

Problem

Solution: Recursion

花花酱 LeetCode 712. Minimum ASCII Delete Sum for Two Strings

Problem

Solution: DP

Solution2: Recursion + Memorization

Related Problems

花花酱 LeetCode 115. Distinct Subsequences

Problem

Solution: DP

Related Problems:

花花酱 LeetCode 836. Rectangle Overlap

Problem

Solution: Geometry

Huahua's Tech Road

花花酱 LeetCode 873. Length of Longest Fibonacci Subsequence

Problem

Solution 1: DP

C++

C++ V2

Solution 2: HashTable

C++

花花酱 LeetCode 872. Leaf-Similar Trees

Problem

Solution: Recursion

花花酱 LeetCode 712. Minimum ASCII Delete Sum for Two Strings

Problem

Solution: DP

Solution2: Recursion + Memorization

Related Problems

花花酱 LeetCode 115. Distinct Subsequences

Problem

Solution: DP

Related Problems:

花花酱 LeetCode 836. Rectangle Overlap

Problem

Solution: Geometry