Problem
题目大意:给你一堵砖墙,求每次击碎一块后掉落的砖头数量。
We have a grid of 1s and 0s; the 1s in a cell represent bricks. A brick will not drop if and only if it is directly connected to the top of the grid, or at least one of its (4-way) adjacent bricks will not drop.
We will do some erasures sequentially. Each time we want to do the erasure at the location (i, j), the brick (if it exists) on that location will disappear, and then some other bricks may drop because of that erasure.
Return an array representing the number of bricks that will drop after each erasure in sequence.
Example 1: Input: grid = [[1,0,0,0],[1,1,1,0]] hits = [[1,0]] Output: [2] Explanation: If we erase the brick at (1, 0), the brick at (1, 1) and (1, 2) will drop. So we should return 2.
Example 2: Input: grid = [[1,0,0,0],[1,1,0,0]] hits = [[1,1],[1,0]] Output: [0,0] Explanation: When we erase the brick at (1, 0), the brick at (1, 1) has already disappeared due to the last move. So each erasure will cause no bricks dropping. Note that the erased brick (1, 0) will not be counted as a dropped brick.
Idea
- For each day, hit and clear the specified brick.
- Find all connected components (CCs) using DFS.
- For each CC, if there is no brick that is on the first row that the entire cc will drop. Clear those CCs.
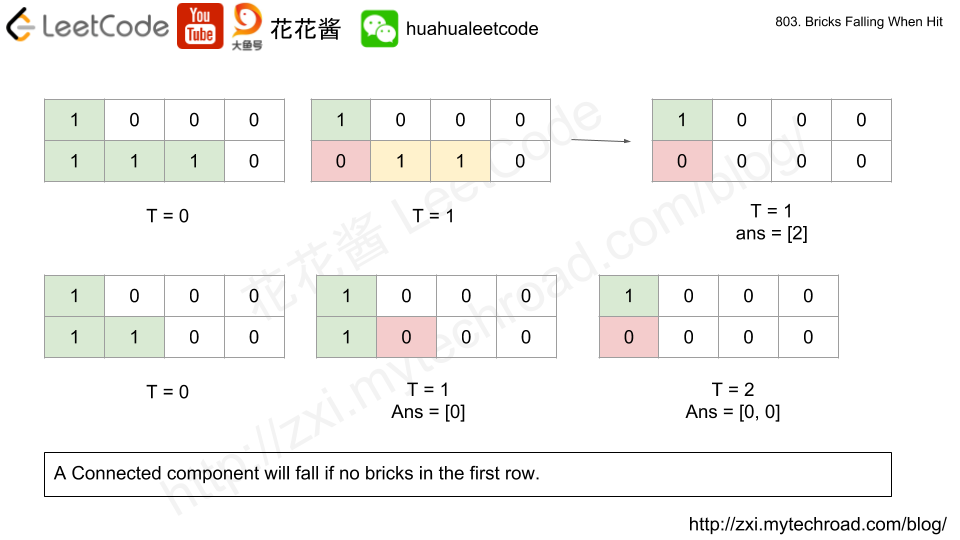
Solution: DFS
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
// Author: Huahua // Running time: 1261 ms class Solution { public: vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) { dirs_ = {0, -1, 0, 1, 0}; m_ = grid.size(); n_ = grid[0].size(); g_.swap(grid); seq_ = 1; vector<int> ans; for (int i = 0; i < hits.size(); ++i) ans.push_back(hit(hits[i][1], hits[i][0])); return ans; } private: vector<vector<int>> g_; vector<int> dirs_; int seq_; int m_; int n_; // hit x, y and return the number of bricks fallen. int hit(int x, int y) { if (x < 0 || x >= n_ || y < 0 || y >= m_) return 0; g_[y][x] = 0; int ans = 0; for (int i = 0; i < 4; ++i) { ++seq_; int count = 0; if (!fall(x + dirs_[i], y + dirs_[i + 1], false, count)) continue; ++seq_; ans += count; fall(x + dirs_[i], y + dirs_[i + 1], true, count); } return ans; } // Check whether the CC contains (x, y) will fall or not. // Set all nodes in this CC as seq_ or 0 if clear. // count: the # of nodes in this CC. bool fall(int x, int y, bool clear, int& count) { if (x < 0 || x >= n_ || y < 0 || y >= m_) return true; if (g_[y][x] == seq_ || g_[y][x] == 0) return true; if (y == 0) return false; g_[y][x] = clear ? 0 : seq_; ++count; for (int i = 0; i < 4; ++i) if (!fall(x + dirs_[i], y + dirs_[i + 1], clear, count)) return false; return true; } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
// Author: Huahua // Stack Overflow (1024 recursive calls) class Solution { int[] dirs = new int[]{0, -1, 0, 1, 0}; int m; int n; int[][] g; int seq; int count; public int[] hitBricks(int[][] grid, int[][] hits) { this.g = grid; this.m = grid.length; this.n = grid[0].length; int[] ans = new int[hits.length]; for (int i = 0; i < hits.length; ++i) ans[i] = hit(hits[i][1], hits[i][0]); return ans; } private int hit(int x, int y) { if (x < 0 || x >= n || y < 0 || y >= m || g[y][x] == 0) return 0; g[y][x] = 0; int ans = 0; for (int i = 0; i < 4; ++i) { ++seq; count = 0; if (!fall(x + dirs[i], y + dirs[i + 1], false)) continue; ans += count; ++seq; fall(x + dirs[i], y + dirs[i + 1], true); } return ans; } private boolean fall(int x, int y, boolean clear) { if (x < 0 || x >= n || y < 0 || y >= m) return true; if (g[y][x] == seq || g[y][x] == 0) return true; if (y == 0) return false; g[y][x] = clear ? 0 : seq; ++count; for (int i = 0; i < 4; ++i) if (!fall(x + dirs[i], y + dirs[i + 1], clear)) return false; return true; } } |