题目大意:给你一个格子地图上面有一些病毒用1表示,未受感染的格子用0表示。带有病毒的格子每天会向四周的格子传播病毒。在每一天,你必须在最大的病毒(连通区域)的周围建造墙阻挡病毒传播。问你一共需要多少个墙才能阻挡所有病毒传播。
Problems:
A virus is spreading rapidly, and your task is to quarantine the infected area by installing walls.
The world is modeled as a 2-D array of cells, where 0 represents uninfected cells, and 1 represents cells contaminated with the virus. A wall (and only one wall) can be installed between any two 4-directionally adjacent cells, on the shared boundary.
Every night, the virus spreads to all neighboring cells in all four directions unless blocked by a wall. Resources are limited. Each day, you can install walls around only one region — the affected area (continuous block of infected cells) that threatens the most uninfected cells the following night. There will never be a tie.
Can you save the day? If so, what is the number of walls required? If not, and the world becomes fully infected, return the number of walls used.
Example 1:
Input: grid = [[0,1,0,0,0,0,0,1], [0,1,0,0,0,0,0,1], [0,0,0,0,0,0,0,1], [0,0,0,0,0,0,0,0]] Output: 10 Explanation: There are 2 contaminated regions. On the first day, add 5 walls to quarantine the viral region on the left. The board after the virus spreads is: [[0,1,0,0,0,0,1,1], [0,1,0,0,0,0,1,1], [0,0,0,0,0,0,1,1], [0,0,0,0,0,0,0,1]] On the second day, add 5 walls to quarantine the viral region on the right. The virus is fully contained.
Example 2:
Input: grid = [[1,1,1], [1,0,1], [1,1,1]] Output: 4 Explanation: Even though there is only one cell saved, there are 4 walls built. Notice that walls are only built on the shared boundary of two different cells.
Example 3:
Input: grid = [[1,1,1,0,0,0,0,0,0], [1,0,1,0,1,1,1,1,1], [1,1,1,0,0,0,0,0,0]] Output: 13 Explanation: The region on the left only builds two new walls.
Note:
- The number of rows and columns of
gridwill each be in the range[1, 50]. - Each
grid[i][j]will be either0or1. - Throughout the described process, there is always a contiguous viral region that will infect strictly more uncontaminated squares in the next round.
Idea:
Use DFS to find virus regions, next affected regions and # of walls needed to block each virus region.
Simulate the virus expansion process.
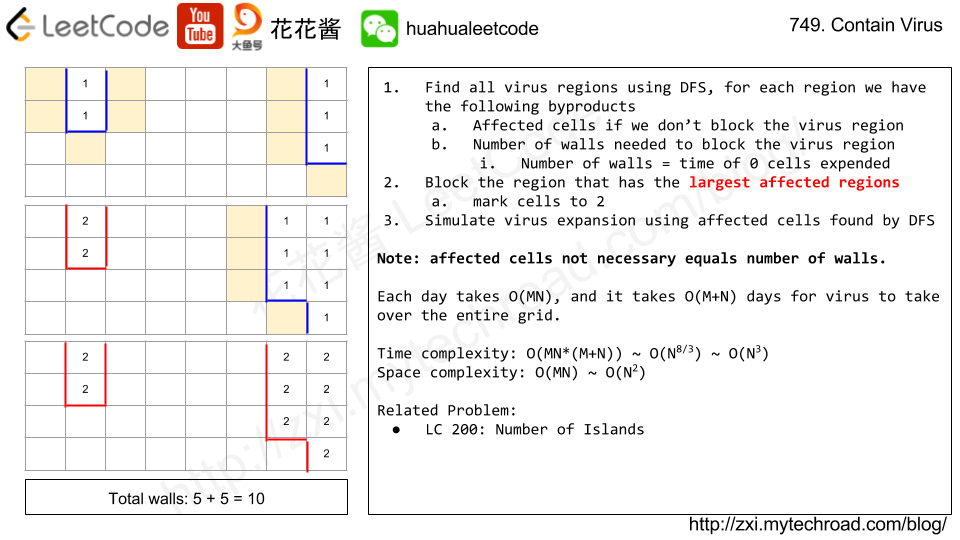
Solution:
C++ / DFS
Time complexity: O(n^3)
Space complexity: O(n^2)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
// Author: Huahua // Runtime: 12 ms class Solution { public: int containVirus(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); int total_walls = 0; while (true) { vector<int> visited(m * n, 0); vector<int> virus_area; vector<unordered_set<int>> nexts; int block_index = -1; int block_walls = -1; for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) { int key = i * n + j; if (grid[i][j] != 1 || visited[key]) continue; vector<int> curr; unordered_set<int> next; int walls = 0; getArea(j, i, m, n, grid, visited, curr, next, walls); if (next.empty()) continue; if (nexts.empty() || next.size() > nexts[block_index].size()) { virus_area.swap(curr); block_index = nexts.size(); block_walls = walls; } nexts.push_back(std::move(next)); } if (nexts.empty()) break; total_walls += block_walls; for (int i = 0; i < nexts.size(); ++i) { if (i == block_index) { for (const int key : virus_area) { int y = key / n; int x = key % n; grid[y][x] = 2; // blocked. } } else { for (const int key : nexts[i]) { int y = key / n; int x = key % n; grid[y][x] = 1; // newly affected } } } } return total_walls; } private: void getArea( int x, int y, int m, int n, vector<vector<int>>& grid, vector<int>& visited, vector<int>& curr, unordered_set<int>& next, int& walls) { static int dirs[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; if (x < 0 || x >= n || y < 0 || y >= m || grid[y][x] == 2) return; int key = y * n + x; // need one wall if (grid[y][x] == 0) { ++walls; next.insert(key); return; } if (visited[key]) return; visited[key] = 1; curr.push_back(key); for (int i = 0; i < 4; ++i) getArea(x + dirs[i][0], y + dirs[i][1], m, n, grid, visited, curr, next, walls); } }; |


