Huahua’s Tech Road

花花酱 LeetCode 2069. Walking Robot Simulation II

By zxi on November 13, 2021

A width x height grid is on an XY-plane with the bottom-left cell at (0, 0) and the top-right cell at (width - 1, height - 1). The grid is aligned with the four cardinal directions ("North", "East", "South", and "West"). A robot is initially at cell (0, 0) facing direction "East".

The robot can be instructed to move for a specific number of steps. For each step, it does the following.

Attempts to move forward one cell in the direction it is facing.
If the cell the robot is moving to is out of bounds, the robot instead turns 90 degrees counterclockwise and retries the step.

After the robot finishes moving the number of steps required, it stops and awaits the next instruction.

Implement the Robot class:

Robot(int width, int height) Initializes the width x height grid with the robot at (0, 0) facing "East".
void move(int num) Instructs the robot to move forward num steps.
int[] getPos() Returns the current cell the robot is at, as an array of length 2, [x, y].
String getDir() Returns the current direction of the robot, "North", "East", "South", or "West".

Example 1:

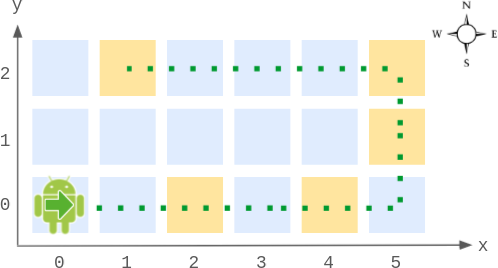
Input
["Robot", "move", "move", "getPos", "getDir", "move", "move", "move", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
Output
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]

Explanation
Robot robot = new Robot(6, 3); // Initialize the grid and the robot at (0, 0) facing East.
robot.move(2);  // It moves two steps East to (2, 0), and faces East.
robot.move(2);  // It moves two steps East to (4, 0), and faces East.
robot.getPos(); // return [4, 0]
robot.getDir(); // return "East"
robot.move(2);  // It moves one step East to (5, 0), and faces East.
                // Moving the next step East would be out of bounds, so it turns and faces North.
                // Then, it moves one step North to (5, 1), and faces North.
robot.move(1);  // It moves one step North to (5, 2), and faces North (not West).
robot.move(4);  // Moving the next step North would be out of bounds, so it turns and faces West.
                // Then, it moves four steps West to (1, 2), and faces West.
robot.getPos(); // return [1, 2]
robot.getDir(); // return "West"

Constraints:

2 <= width, height <= 100
1 <= num <= 10⁵
At most 10⁴ calls in total will be made to move, getPos, and getDir.

Solution: Simulation

Note num >> w + h, when we hit a wall, we will always follow the boundary afterwards. We can do num %= p to reduce steps, where p = ((w – 1) + (h – 1)) * 2

Time complexity: move: O(min(num, w+h))
Space complexity: O(1)

C++

// Author: Huahua

constexpr static int dirs[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

const static vector<string> kNames{"East", "North", "West", "South"};

class Robot {

public:

Robot(int width, int height): w_(width), h_(height) {

p_ = ((w_ - 1) + (h_ - 1)) * 2;

}

void move(int num) {

while (num) {

int tx = x_ + dirs[d_][0];

int ty = y_ + dirs[d_][1];

if (tx < 0 || tx >= w_ || ty < 0 || ty >= h_) {

if (num > p_) num %= p_;

if (num) d_ = (d_ + 1) % 4;

continue;

}

x_ = tx;

y_ = ty;

--num;

}

vector<int> getPos() { return {x_, y_}; }

string getDir() { return kNames[d_]; }

private:

int w_;

int h_;

int d_{0}; // 0: E, 1: N, 2: W, 3: S

int x_{0};

int y_{0};

int p_{0};

};

花花酱 LeetCode 2068. Check Whether Two Strings are Almost Equivalent

By zxi on November 13, 2021

Two strings word1 and word2 are considered almost equivalent if the differences between the frequencies of each letter from 'a' to 'z' between word1 and word2 is at most 3.

Given two strings word1 and word2, each of length n, return true if word1 and word2 are almost equivalent, or false otherwise.

The frequency of a letter x is the number of times it occurs in the string.

Example 1:

Input: word1 = "aaaa", word2 = "bccb"
Output: false
Explanation: There are 4 'a's in "aaaa" but 0 'a's in "bccb".
The difference is 4, which is more than the allowed 3.

Example 2:

Input: word1 = "abcdeef", word2 = "abaaacc"
Output: true
Explanation: The differences between the frequencies of each letter in word1 and word2 are at most 3:
- 'a' appears 1 time in word1 and 4 times in word2. The difference is 3.
- 'b' appears 1 time in word1 and 1 time in word2. The difference is 0.
- 'c' appears 1 time in word1 and 2 times in word2. The difference is 1.
- 'd' appears 1 time in word1 and 0 times in word2. The difference is 1.
- 'e' appears 2 times in word1 and 0 times in word2. The difference is 2.
- 'f' appears 1 time in word1 and 0 times in word2. The difference is 1.

Example 3:

Input: word1 = "cccddabba", word2 = "babababab"
Output: true
Explanation: The differences between the frequencies of each letter in word1 and word2 are at most 3:
- 'a' appears 2 times in word1 and 4 times in word2. The difference is 2.
- 'b' appears 2 times in word1 and 5 times in word2. The difference is 3.
- 'c' appears 3 times in word1 and 0 times in word2. The difference is 3.
- 'd' appears 2 times in word1 and 0 times in word2. The difference is 2.

Constraints:

n == word1.length == word2.length
1 <= n <= 100
word1 and word2 consist only of lowercase English letters.

Solution: Hashtable

Use a hashtable to track the relative frequency of a letter.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool checkAlmostEquivalent(string word1, string word2) {

vector<int> m(26);

for (char c: word1) ++m[c - 'a'];

for (char c: word2) --m[c - 'a'];

for (int i = 0; i < 26; ++i)

if (abs(m[i]) > 3) return false;

return true;

}

};

花花酱 LeetCode 2065. Maximum Path Quality of a Graph

By zxi on November 7, 2021

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the i^th node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [u_j, v_j, time_j] indicates that there is an undirected edge between the nodes u_j and v_j,and it takes time_j seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node’s value is added at most once to the sum).

Return the maximum quality of a valid path.

Note: There are at most four edges connected to each node.

Example 1:

Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2:

Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3:

Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Example 4:

Input: values = [0,1,2], edges = [[1,2,10]], maxTime = 10
Output: 0
Explanation: 
The only path is 0. The total time taken is 0.
The only node visited is 0, giving a maximal path quality of 0.

Constraints:

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
All the pairs [u_j, v_j] are unique.
There are at most four edges connected to each node.
The graph may not be connected.

Solution: DFS

Given time >= 10 and maxTime <= 100, the path length is at most 10, given at most four edges connected to each node.
Time complexity: O(4¹⁰)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {

const int n = values.size();

vector<vector<pair<int, int>>> g(n);

for (const auto& e : edges) {

g[e[0]].emplace_back(e[1], e[2]);

g[e[1]].emplace_back(e[0], e[2]);

}

vector<int> seen(n);

int ans = 0;

function<void(int, int, int)> dfs = [&](int u, int t, int s) {

if (++seen[u] == 1) s += values[u];

if (u == 0) ans = max(ans, s);

for (auto [v, d] : g[u])

if (t + d <= maxTime) dfs(v, t + d, s);

if (--seen[u] == 0) s -= values[u];

};

dfs(0, 0, 0);

return ans;

}

};

花花酱 LeetCode 2064. Minimized Maximum of Products Distributed to Any Store

By zxi on November 7, 2021

You are given an integer n indicating there are n specialty retail stores. There are m product types of varying amounts, which are given as a 0-indexed integer array quantities, where quantities[i] represents the number of products of the i^th product type.

You need to distribute all products to the retail stores following these rules:

A store can only be given at most one product type but can be given any amount of it.
After distribution, each store will be given some number of products (possibly 0). Let x represent the maximum number of products given to any store. You want x to be as small as possible, i.e., you want to minimize the maximum number of products that are given to any store.

Return the minimum possible x.

Example 1:

Input: n = 6, quantities = [11,6]
Output: 3
Explanation: One optimal way is:
- The 11 products of type 0 are distributed to the first four stores in these amounts: 2, 3, 3, 3
- The 6 products of type 1 are distributed to the other two stores in these amounts: 3, 3
The maximum number of products given to any store is max(2, 3, 3, 3, 3, 3) = 3.

Example 2:

Input: n = 7, quantities = [15,10,10]
Output: 5
Explanation: One optimal way is:
- The 15 products of type 0 are distributed to the first three stores in these amounts: 5, 5, 5
- The 10 products of type 1 are distributed to the next two stores in these amounts: 5, 5
- The 10 products of type 2 are distributed to the last two stores in these amounts: 5, 5
The maximum number of products given to any store is max(5, 5, 5, 5, 5, 5, 5) = 5.

Example 3:

Input: n = 1, quantities = [100000]
Output: 100000
Explanation: The only optimal way is:
- The 100000 products of type 0 are distributed to the only store.
The maximum number of products given to any store is max(100000) = 100000.

Constraints:

m == quantities.length
1 <= m <= n <= 10⁵
1 <= quantities[i] <= 10⁵

Solution: Binary Search

Find the smallest max product s.t. all products can be distribute to <= n stores.

Time complexity: O(nlog(max(q)))
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minimizedMaximum(int n, vector<int>& quantities) {

int l = 1;

int r = *max_element(begin(quantities), end(quantities)) + 1;

while (l < r) {

int cur = 0;

int m = l + (r - l) / 2;

for (int q : quantities)

cur += (q + (m - 1)) / m;

if (cur <= n)

r = m;

else

l = m + 1;

}

return l;

}

};

花花酱 LeetCode 2063. Vowels of All Substrings

By zxi on November 7, 2021

Given a string word, return the sum of the number of vowels ('a', 'e', 'i', 'o', and 'u') in every substring of word.

A substring is a contiguous (non-empty) sequence of characters within a string.

Note: Due to the large constraints, the answer may not fit in a signed 32-bit integer. Please be careful during the calculations.

Example 1:

Input: word = "aba"
Output: 6
Explanation: 
All possible substrings are: "a", "ab", "aba", "b", "ba", and "a".
- "b" has 0 vowels in it
- "a", "ab", "ba", and "a" have 1 vowel each
- "aba" has 2 vowels in it
Hence, the total sum of vowels = 0 + 1 + 1 + 1 + 1 + 2 = 6.

Example 2:

Input: word = "abc"
Output: 3
Explanation: 
All possible substrings are: "a", "ab", "abc", "b", "bc", and "c".
- "a", "ab", and "abc" have 1 vowel each
- "b", "bc", and "c" have 0 vowels each
Hence, the total sum of vowels = 1 + 1 + 1 + 0 + 0 + 0 = 3.

Example 3:

Input: word = "ltcd"
Output: 0
Explanation: There are no vowels in any substring of "ltcd".

Example 4:

Input: word = "noosabasboosa"
Output: 237
Explanation: There are a total of 237 vowels in all the substrings.

Constraints:

1 <= word.length <= 10⁵
word consists of lowercase English letters.

Solution: Math

For a vowel at index i,
we can choose 0, 1, … i as starting point
choose i, i+1, …, n -1 as end point.
There will be (i – 0 + 1) * (n – 1 – i + 1) possible substrings that contains word[i].

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

long long countVowels(string word) {

const long long n = word.size();

long long ans = 0;

for (long long i = 0; i < n; ++i) {

switch (word[i]) {

case 'a':

case 'e':

case 'i':

case 'o':

case 'u':

ans += (i + 1) * (n - 1 - i + 1);

break;

}

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 2069. Walking Robot Simulation II

Solution: Simulation

C++

花花酱 LeetCode 2068. Check Whether Two Strings are Almost Equivalent

Solution: Hashtable

C++

花花酱 LeetCode 2065. Maximum Path Quality of a Graph

Solution: DFS

C++

花花酱 LeetCode 2064. Minimized Maximum of Products Distributed to Any Store

Solution: Binary Search

C++

花花酱 LeetCode 2063. Vowels of All Substrings

Solution: Math

C++