Huahua’s Tech Road

花花酱 LeetCode 2065. Maximum Path Quality of a Graph

By zxi on November 7, 2021

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the i^th node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [u_j, v_j, time_j] indicates that there is an undirected edge between the nodes u_j and v_j,and it takes time_j seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node’s value is added at most once to the sum).

Return the maximum quality of a valid path.

Note: There are at most four edges connected to each node.

Example 1:

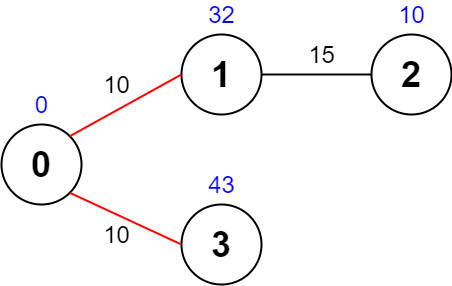
Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2:

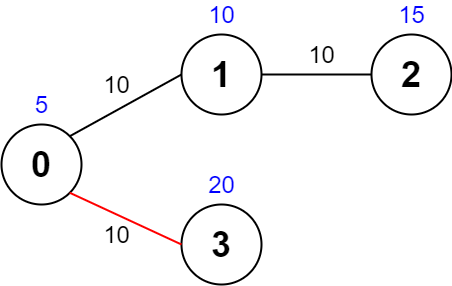
Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3:

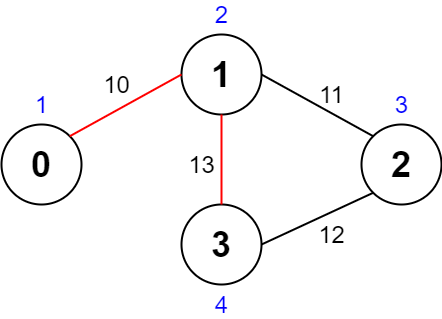
Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Example 4:

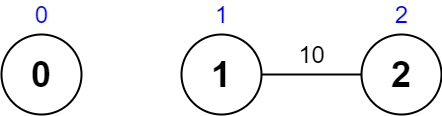
Input: values = [0,1,2], edges = [[1,2,10]], maxTime = 10
Output: 0
Explanation: 
The only path is 0. The total time taken is 0.
The only node visited is 0, giving a maximal path quality of 0.

Constraints:

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
All the pairs [u_j, v_j] are unique.
There are at most four edges connected to each node.
The graph may not be connected.

Solution: DFS

Given time >= 10 and maxTime <= 100, the path length is at most 10, given at most four edges connected to each node.
Time complexity: O(4¹⁰)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {

const int n = values.size();

vector<vector<pair<int, int>>> g(n);

for (const auto& e : edges) {

g[e[0]].emplace_back(e[1], e[2]);

g[e[1]].emplace_back(e[0], e[2]);

}

vector<int> seen(n);

int ans = 0;

function<void(int, int, int)> dfs = [&](int u, int t, int s) {

if (++seen[u] == 1) s += values[u];

if (u == 0) ans = max(ans, s);

for (auto [v, d] : g[u])

if (t + d <= maxTime) dfs(v, t + d, s);

if (--seen[u] == 0) s -= values[u];

};

dfs(0, 0, 0);

return ans;

}

};

花花酱 LeetCode 2064. Minimized Maximum of Products Distributed to Any Store

By zxi on November 7, 2021

You are given an integer n indicating there are n specialty retail stores. There are m product types of varying amounts, which are given as a 0-indexed integer array quantities, where quantities[i] represents the number of products of the i^th product type.

You need to distribute all products to the retail stores following these rules:

A store can only be given at most one product type but can be given any amount of it.
After distribution, each store will be given some number of products (possibly 0). Let x represent the maximum number of products given to any store. You want x to be as small as possible, i.e., you want to minimize the maximum number of products that are given to any store.

Return the minimum possible x.

Example 1:

Input: n = 6, quantities = [11,6]
Output: 3
Explanation: One optimal way is:
- The 11 products of type 0 are distributed to the first four stores in these amounts: 2, 3, 3, 3
- The 6 products of type 1 are distributed to the other two stores in these amounts: 3, 3
The maximum number of products given to any store is max(2, 3, 3, 3, 3, 3) = 3.

Example 2:

Input: n = 7, quantities = [15,10,10]
Output: 5
Explanation: One optimal way is:
- The 15 products of type 0 are distributed to the first three stores in these amounts: 5, 5, 5
- The 10 products of type 1 are distributed to the next two stores in these amounts: 5, 5
- The 10 products of type 2 are distributed to the last two stores in these amounts: 5, 5
The maximum number of products given to any store is max(5, 5, 5, 5, 5, 5, 5) = 5.

Example 3:

Input: n = 1, quantities = [100000]
Output: 100000
Explanation: The only optimal way is:
- The 100000 products of type 0 are distributed to the only store.
The maximum number of products given to any store is max(100000) = 100000.

Constraints:

m == quantities.length
1 <= m <= n <= 10⁵
1 <= quantities[i] <= 10⁵

Solution: Binary Search

Find the smallest max product s.t. all products can be distribute to <= n stores.

Time complexity: O(nlog(max(q)))
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minimizedMaximum(int n, vector<int>& quantities) {

int l = 1;

int r = *max_element(begin(quantities), end(quantities)) + 1;

while (l < r) {

int cur = 0;

int m = l + (r - l) / 2;

for (int q : quantities)

cur += (q + (m - 1)) / m;

if (cur <= n)

r = m;

else

l = m + 1;

}

return l;

}

};

花花酱 LeetCode 2063. Vowels of All Substrings

By zxi on November 7, 2021

Given a string word, return the sum of the number of vowels ('a', 'e', 'i', 'o', and 'u') in every substring of word.

A substring is a contiguous (non-empty) sequence of characters within a string.

Note: Due to the large constraints, the answer may not fit in a signed 32-bit integer. Please be careful during the calculations.

Example 1:

Input: word = "aba"
Output: 6
Explanation: 
All possible substrings are: "a", "ab", "aba", "b", "ba", and "a".
- "b" has 0 vowels in it
- "a", "ab", "ba", and "a" have 1 vowel each
- "aba" has 2 vowels in it
Hence, the total sum of vowels = 0 + 1 + 1 + 1 + 1 + 2 = 6.

Example 2:

Input: word = "abc"
Output: 3
Explanation: 
All possible substrings are: "a", "ab", "abc", "b", "bc", and "c".
- "a", "ab", and "abc" have 1 vowel each
- "b", "bc", and "c" have 0 vowels each
Hence, the total sum of vowels = 1 + 1 + 1 + 0 + 0 + 0 = 3.

Example 3:

Input: word = "ltcd"
Output: 0
Explanation: There are no vowels in any substring of "ltcd".

Example 4:

Input: word = "noosabasboosa"
Output: 237
Explanation: There are a total of 237 vowels in all the substrings.

Constraints:

1 <= word.length <= 10⁵
word consists of lowercase English letters.

Solution: Math

For a vowel at index i,
we can choose 0, 1, … i as starting point
choose i, i+1, …, n -1 as end point.
There will be (i – 0 + 1) * (n – 1 – i + 1) possible substrings that contains word[i].

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

long long countVowels(string word) {

const long long n = word.size();

long long ans = 0;

for (long long i = 0; i < n; ++i) {

switch (word[i]) {

case 'a':

case 'e':

case 'i':

case 'o':

case 'u':

ans += (i + 1) * (n - 1 - i + 1);

break;

}

return ans;

}

};

花花酱 LeetCode 2062. Count Vowel Substrings of a String

By zxi on November 7, 2021

A substring is a contiguous (non-empty) sequence of characters within a string.

A vowel substring is a substring that only consists of vowels ('a', 'e', 'i', 'o', and 'u') and has all five vowels present in it.

Given a string word, return the number of vowel substrings in word.

Example 1:

Input: word = "aeiouu"
Output: 2
Explanation: The vowel substrings of word are as follows (underlined):
- "aeiouu"
- "aeiouu"

Example 2:

Input: word = "unicornarihan"
Output: 0
Explanation: Not all 5 vowels are present, so there are no vowel substrings.

Example 3:

Input: word = "cuaieuouac"
Output: 7
Explanation: The vowel substrings of word are as follows (underlined):
- "cuaieuouac"
- "cuaieuouac"
- "cuaieuouac"
- "cuaieuouac"
- "cuaieuouac"
- "cuaieuouac"
- "cuaieuouac"

Example 4:

Input: word = "bbaeixoubb"
Output: 0
Explanation: The only substrings that contain all five vowels also contain consonants, so there are no vowel substrings.

Constraints:

1 <= word.length <= 100
word consists of lowercase English letters only.

Solution 1: Brute Force

Time complexity: O(n²)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countVowelSubstrings(string_view word) {

const int n = word.size();

auto check = [&](string_view s) {

set<int> seen;

string vowels {"aeiou"};

for (char c : s) {

if (vowels.find(c) == string::npos) return false;

seen.insert(c);

}

return seen.size() == 5;

};

int ans = 0;

for (int i = 0; i < n; ++i)

for (int l = 5; i + l <= n; ++l)

if (check(word.substr(i, l))) ++ans;

return ans;

}

};

Solution 2: Sliding Window / Three Pointers

Maintain a window [i, j] that contain all 5 vowels, find k s.t. [k + 1, i] no longer container 5 vowels.
# of valid substrings end with j will be (k – i).

##aeiouaeioo##
..i....k...j..
i = 3, k = 8, j = 12

Valid substrings are:
aeiouaeioo .eiouaeioo ..iouaeioo ...ouaeioo ....uaeioo
8 – 3 = 5

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countVowelSubstrings(string_view word) {

constexpr string_view vowels{"aeiou"};

int ans = 0;

unordered_map<char, int> m;

for (char c : vowels) m[c] = 0;

for (size_t i = 0, j = 0, k = 0, v = 0; j < word.size(); ++j) {

if (m.count(word[j])) {

v += (++m[word[j]] == 1);

while (v == 5)

v -= (--m[word[k++]] == 0);

ans += k - i;

} else {

for (char c : vowels) m[c] = 0;

v = 0;

i = k = j + 1;

}

return ans;

}

};

花花酱 LeetCode 2059. Minimum Operations to Convert Number

By zxi on November 4, 2021

You are given a 0-indexed integer array nums containing distinct numbers, an integer start, and an integer goal. There is an integer x that is initially set to start, and you want to perform operations on x such that it is converted to goal. You can perform the following operation repeatedly on the number x:

If 0 <= x <= 1000, then for any index i in the array (0 <= i < nums.length), you can set x to any of the following:

x + nums[i]
x - nums[i]
x ^ nums[i] (bitwise-XOR)

Note that you can use each nums[i] any number of times in any order. Operations that set x to be out of the range 0 <= x <= 1000 are valid, but no more operations can be done afterward.

Return the minimum number of operations needed to convert x = start into goal, and -1 if it is not possible.

Example 1:

Input: nums = [1,3], start = 6, goal = 4
Output: 2
Explanation:
We can go from 6 → 7 → 4 with the following 2 operations.
- 6 ^ 1 = 7
- 7 ^ 3 = 4

Example 2:

Input: nums = [2,4,12], start = 2, goal = 12
Output: 2
Explanation:
We can go from 2 → 14 → 12 with the following 2 operations.
- 2 + 12 = 14
- 14 - 2 = 12

Example 3:

Input: nums = [3,5,7], start = 0, goal = -4
Output: 2
Explanation:
We can go from 0 → 3 → -4 with the following 2 operations. 
- 0 + 3 = 3
- 3 - 7 = -4
Note that the last operation sets x out of the range 0 <= x <= 1000, which is valid.

Example 4:

Input: nums = [2,8,16], start = 0, goal = 1
Output: -1
Explanation:
There is no way to convert 0 into 1.

Example 5:

Input: nums = [1], start = 0, goal = 3

Output: 3

Explanation:

We can go from 0 → 1 → 2 → 3 with the following 3 operations.

- 0 + 1 = 1

- 1 + 1 = 2

- 2 + 1 = 3

Constraints:

1 <= nums.length <= 1000
-10⁹ <= nums[i], goal <= 10⁹
0 <= start <= 1000
start != goal
All the integers in nums are distinct.

Solution: BFS

Time complexity: O(n*m)
Space complexity: O(m)

C++

// Author: Huahua

class Solution {

public:

int minimumOperations(vector<int>& nums, int start, int goal) {

vector<int> seen(1001);

queue<int> q{{start}};

for (int ans = 1, s = 1; !q.empty(); ++ans, s = q.size()) {

while (s--) {

int x = q.front(); q.pop();

for (int n : nums)

for (int t : {x + n, x - n, x ^ n})

if (t == goal)

return ans;

else if (t < 0 || t > 1000 || seen[t]++)

continue;

else

q.push(t);

}

return -1;

}

};

Huahua's Tech Road

花花酱 LeetCode 2065. Maximum Path Quality of a Graph

Solution: DFS

C++

花花酱 LeetCode 2064. Minimized Maximum of Products Distributed to Any Store

Solution: Binary Search

C++

花花酱 LeetCode 2063. Vowels of All Substrings

Solution: Math

C++

花花酱 LeetCode 2062. Count Vowel Substrings of a String

C++

Solution 2: Sliding Window / Three Pointers

C++

花花酱 LeetCode 2059. Minimum Operations to Convert Number

Solution: BFS

C++