Huahua’s Tech Road

花花酱 LeetCode 1805. Number of Different Integers in a String

By zxi on March 27, 2021

You are given a string word that consists of digits and lowercase English letters.

You will replace every non-digit character with a space. For example, "a123bc34d8ef34" will become " 123 34 8 34". Notice that you are left with some integers that are separated by at least one space: "123", "34", "8", and "34".

Return the number of different integers after performing the replacement operations on word.

Two integers are considered different if their decimal representations without any leading zeros are different.

Example 1:

Input: word = "a123bc34d8ef34"
Output: 3
Explanation: The three different integers are "123", "34", and "8". Notice that "34" is only counted once.

Example 2:

Input: word = "leet1234code234"
Output: 2

Example 3:

Input: word = "a1b01c001"
Output: 1
Explanation: The three integers "1", "01", and "001" all represent the same integer because
the leading zeros are ignored when comparing their decimal values.

Constraints:

1 <= word.length <= 1000
word consists of digits and lowercase English letters.

Solution: Hashtable

Be careful about leading zeros.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int numDifferentIntegers(string word) {

word += "$";

unordered_set<string> s;

deque<char> cur;

for (char c : word) {

if (isdigit(c)) {

cur.push_back(c);

} else if (!cur.empty()) {

while (cur.size() > 1 && cur[0] == '0')

cur.pop_front();

s.insert({begin(cur), end(cur)});

cur.clear();

}

return s.size();

}

};

花花酱 LeetCode 1802. Maximum Value at a Given Index in a Bounded Array

By zxi on March 22, 2021

You are given three positive integers n, index and maxSum. You want to construct an array nums (0-indexed) that satisfies the following conditions:

nums.length == n
nums[i] is a positive integer where 0 <= i < n.
abs(nums[i] - nums[i+1]) <= 1 where 0 <= i < n-1.
The sum of all the elements of nums does not exceed maxSum.
nums[index] is maximized.

Return nums[index] of the constructed array.

Note that abs(x) equals x if x >= 0, and -x otherwise.

Example 1:

Input: n = 4, index = 2,  maxSum = 6
Output: 2
Explanation: The arrays [1,1,2,1] and [1,2,2,1] satisfy all the conditions. There are no other valid arrays with a larger value at the given index.

Example 2:

Input: n = 6, index = 1,  maxSum = 10
Output: 3

Constraints:

1 <= n <= maxSum <= 10⁹
0 <= index < n

Solution: Binary Search

To maximize nums[index], we can construct an array like this:
[1, 1, 1, …, 1, 2, 3, …, k – 1, k, k – 1, …,3, 2, 1, …., 1, 1, 1]

Time complexity: O(logn)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int maxValue(int n, int index, int maxSum) {

int l = 1;

int r = maxSum + 1;

while (l < r) {

int64_t m = l + (r - l) / 2;

int64_t t1 = m - index;

int64_t t2 = m - (n - 1 - index);

int64_t s1 = (t1 + m) * (index + 1) / 2;

int64_t s2 = (m + t2) * (n - index) / 2;

if (t1 <= 0) s1 = (1 + m) * m / 2 + (index - m + 1);

if (t2 <= 0) s2 = (1 + m) * m / 2 + (n - index - m);

if (s1 + s2 - m > maxSum)

r = m;

else

l = m + 1;

}

return l - 1;

}

};

LeetCode 1801. Number of Orders in the Backlog

By zxi on March 21, 2021

You are given a 2D integer array orders, where each orders[i] = [price_i, amount_i, orderType_i] denotes that amount_iorders have been placed of type orderType_i at the price price_i. The orderType_i is:

0 if it is a batch of buy orders, or
1 if it is a batch of sell orders.

Note that orders[i] represents a batch of amount_i independent orders with the same price and order type. All orders represented by orders[i] will be placed before all orders represented by orders[i+1] for all valid i.

There is a backlog that consists of orders that have not been executed. The backlog is initially empty. When an order is placed, the following happens:

If the order is a buy order, you look at the sell order with the smallest price in the backlog. If that sell order’s price is smaller than or equal to the current buy order’s price, they will match and be executed, and that sell order will be removed from the backlog. Else, the buy order is added to the backlog.
Vice versa, if the order is a sell order, you look at the buy order with the largest price in the backlog. If that buy order’s price is larger than or equal to the current sell order’s price, they will match and be executed, and that buy order will be removed from the backlog. Else, the sell order is added to the backlog.

Return the total amount of orders in the backlog after placing all the orders from the input. Since this number can be large, return it modulo 10⁹ + 7.

Example 1: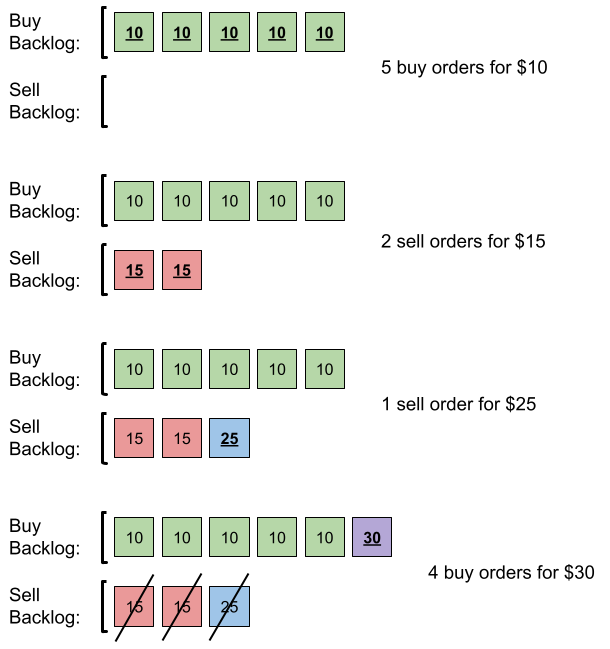

Input: orders = [[10,5,0],[15,2,1],[25,1,1],[30,4,0]]
Output: 6
Explanation: Here is what happens with the orders:
- 5 orders of type buy with price 10 are placed. There are no sell orders, so the 5 orders are added to the backlog.
- 2 orders of type sell with price 15 are placed. There are no buy orders with prices larger than or equal to 15, so the 2 orders are added to the backlog.
- 1 order of type sell with price 25 is placed. There are no buy orders with prices larger than or equal to 25 in the backlog, so this order is added to the backlog.
- 4 orders of type buy with price 30 are placed. The first 2 orders are matched with the 2 sell orders of the least price, which is 15 and these 2 sell orders are removed from the backlog. The 3^rd order is matched with the sell order of the least price, which is 25 and this sell order is removed from the backlog. Then, there are no more sell orders in the backlog, so the 4^th order is added to the backlog.
Finally, the backlog has 5 buy orders with price 10, and 1 buy order with price 30. So the total number of orders in the backlog is 6.

Example 2: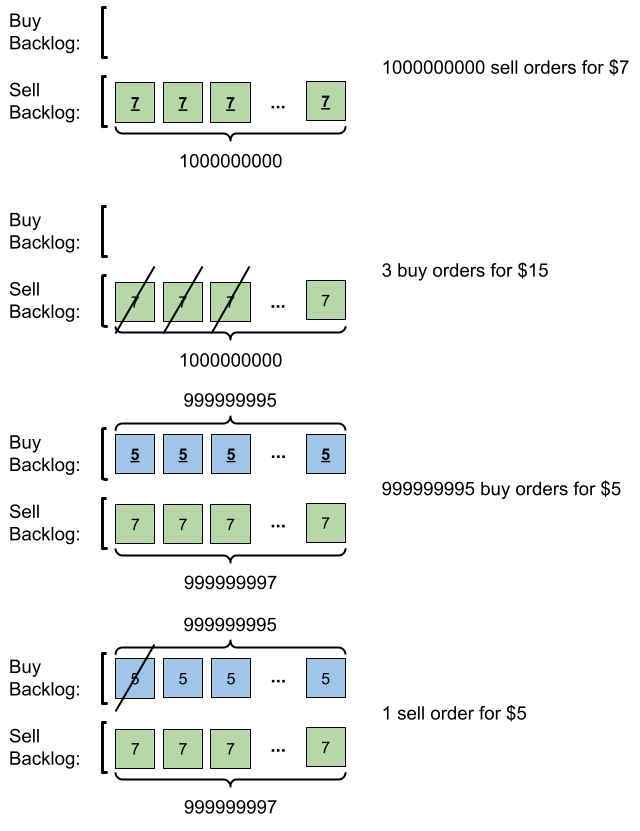

Input: orders = [[7,1000000000,1],[15,3,0],[5,999999995,0],[5,1,1]]
Output: 999999984
Explanation: Here is what happens with the orders:
- 10⁹ orders of type sell with price 7 are placed. There are no buy orders, so the 10⁹ orders are added to the backlog.
- 3 orders of type buy with price 15 are placed. They are matched with the 3 sell orders with the least price which is 7, and those 3 sell orders are removed from the backlog.
- 999999995 orders of type buy with price 5 are placed. The least price of a sell order is 7, so the 999999995 orders are added to the backlog.
- 1 order of type sell with price 5 is placed. It is matched with the buy order of the highest price, which is 5, and that buy order is removed from the backlog.
Finally, the backlog has (1000000000-3) sell orders with price 7, and (999999995-1) buy orders with price 5. So the total number of orders = 1999999991, which is equal to 999999984 % (10⁹ + 7).

Constraints:

1 <= orders.length <= 10⁵
orders[i].length == 3
1 <= price_i, amount_i <= 10⁹
orderType_i is either 0 or 1.

Solution: Treemap / PriorityQueue / Heap

buy backlog: max heap
sell backlog: min heap
Trade happens between the tops of two queues.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int getNumberOfBacklogOrders(vector<vector<int>>& orders) {

constexpr int kMod = 1e9 + 7;

map<int64_t, int64_t> buys;

map<int64_t, int64_t> sells;

for (const auto& order : orders) {

auto& m = order[2] == 0 ? buys : sells;

m[order[0]] += order[1];

while (buys.size() && sells.size()) {

auto b = rbegin(buys);

auto s = begin(sells);

if (b->first < s->first) break;

const int k = min(b->second, s->second);

if (!(b->second -= k)) buys.erase((++b).base());

if (!(s->second -= k)) sells.erase(s);

}

int64_t ans = 0;

for (const auto& [p, c] : buys) ans += c;

for (const auto& [p, c] : sells) ans += c;

return ans % kMod;

}

};

花花酱 LeetCode 1800. Maximum Ascending Subarray Sum

By zxi on March 21, 2021

Given an array of positive integers nums, return the maximum possible sum of an ascending subarray in nums.

A subarray is defined as a contiguous sequence of numbers in an array.

A subarray [nums_l, nums_l+1, ..., nums_r-1, nums_r] is ascending if for all i where l <= i < r, nums_i< nums_i+1. Note that a subarray of size 1 is ascending.

Example 1:

Input: nums = [10,20,30,5,10,50]
Output: 65
Explanation: [5,10,50] is the ascending subarray with the maximum sum of 65.

Example 2:

Input: nums = [10,20,30,40,50]
Output: 150
Explanation: [10,20,30,40,50] is the ascending subarray with the maximum sum of 150.

Example 3:

Input: nums = [12,17,15,13,10,11,12]
Output: 33
Explanation: [10,11,12] is the ascending subarray with the maximum sum of 33.

Example 4:

Input: nums = [100,10,1]
Output: 100

Constraints:

1 <= nums.length <= 100
1 <= nums[i] <= 100

Solution: Running sum with resetting

Time complexity: O(n)
Space complexity: O(1)

Track the running sum and reset it to zero if nums[i] <= nums[i – 1]

C++

// Author: Huahua

class Solution {

public:

int maxAscendingSum(vector<int>& nums) {

int ans = 0;

for (int i = 0, s = 0; i < nums.size(); ++i) {

if (i && nums[i] <= nums[i - 1])

s = 0;

ans = max(ans, s += nums[i]);

}

return ans;

}

};

花花酱 LeetCode 1799. Maximize Score After N Operations

By zxi on March 20, 2021

You are given nums, an array of positive integers of size 2 * n. You must perform n operations on this array.

In the i^th operation (1-indexed), you will:

Choose two elements, x and y.
Receive a score of i * gcd(x, y).
Remove x and y from nums.

Return the maximum score you can receive after performing n operations.

The function gcd(x, y) is the greatest common divisor of x and y.

Example 1:

Input: nums = [1,2]
Output: 1
Explanation: The optimal choice of operations is:
(1 * gcd(1, 2)) = 1

Example 2:

Input: nums = [3,4,6,8]
Output: 11
Explanation: The optimal choice of operations is:
(1 * gcd(3, 6)) + (2 * gcd(4, 8)) = 3 + 8 = 11

Example 3:

Input: nums = [1,2,3,4,5,6]
Output: 14
Explanation: The optimal choice of operations is:
(1 * gcd(1, 5)) + (2 * gcd(2, 4)) + (3 * gcd(3, 6)) = 1 + 4 + 9 = 14

Constraints:

1 <= n <= 7
nums.length == 2 * n
1 <= nums[i] <= 10⁶

Solution: Mask DP

dp(mask, i) := max score of numbers (represented by a binary mask) at the i-th operations.
ans = dp(1, mask)
base case: dp = 0 if mask == 0
Transition: dp(mask, i) = max(dp(new_mask, i + 1) + i * gcd(nums[m], nums[n]))

Time complexity: O(n²*2²ⁿ)
Space complexity: O(2²ⁿ)

C++

// Author: Huahua, 184 ms, 8.3 MB

class Solution {

public:

int maxScore(vector<int>& nums) {

const int l = nums.size();

vector<int> cache(1 << l);

function<int(int)> dp = [&](int mask) {

if (mask == 0) return 0;

int& ans = cache[mask];

if (ans > 0) return ans;

const int k = (l - __builtin_popcount(mask)) / 2 + 1;

for (int i = 0; i < l; ++i)

for (int j = i + 1; j < l; ++j)

if ((mask & (1 << i)) && (mask & (1 << j)))

ans = max(ans, k * gcd(nums[i], nums[j])

+ dp(mask ^ (1 << i) ^ (1 << j)));

return ans;

};

return dp((1 << l) - 1);

}

};

Bottom-Up

C++

// Author: Huahua, 156 ms, 8.3 MB

class Solution {

public:

int maxScore(vector<int>& nums) {

const int l = nums.size();

vector<int> dp(1 << l);

for (int mask = 0; mask < 1 << l; ++mask) {

int c = __builtin_popcount(mask);

if (c & 1) continue; // only do in pairs

int k = c / 2 + 1;

for (int i = 0; i < l; ++i)

for (int j = i + 1; j < l; ++j)

if ((mask & (1 << i)) + (mask & (1 << j)) == 0) {

int new_mask = mask | (1 << i) | (1 << j);

dp[new_mask] = max(dp[new_mask],

k * gcd(nums[i], nums[j]) + dp[mask]);

}

return dp[(1 << l) - 1];

}

};

Huahua's Tech Road

花花酱 LeetCode 1805. Number of Different Integers in a String

Solution: Hashtable

C++

花花酱 LeetCode 1802. Maximum Value at a Given Index in a Bounded Array

Solution: Binary Search

C++

LeetCode 1801. Number of Orders in the Backlog

Solution: Treemap / PriorityQueue / Heap

C++

花花酱 LeetCode 1800. Maximum Ascending Subarray Sum

Solution: Running sum with resetting

C++

花花酱 LeetCode 1799. Maximize Score After N Operations

Solution: Mask DP

C++

C++