Given a 2D grid of size n * m and an integer k. You need to shift the grid k times.
In one shift operation:
- Element at
grid[i][j]becomes atgrid[i][j + 1]. - Element at
grid[i][m - 1]becomes atgrid[i + 1][0]. - Element at
grid[n - 1][m - 1]becomes atgrid[0][0].
Return the 2D grid after applying shift operation k times.
Example 1:
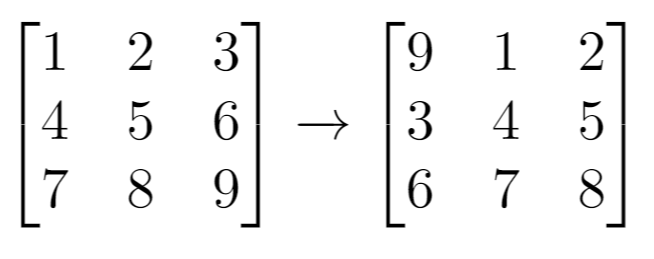
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]
Example 2:
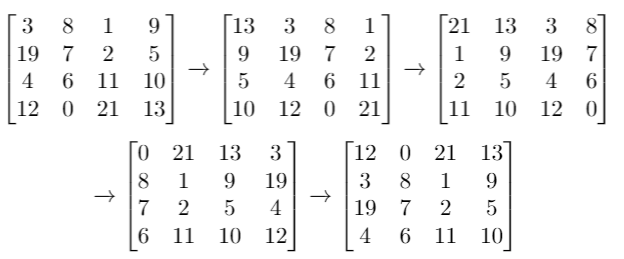
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]
Example 3:
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]
Constraints:
1 <= grid.length <= 501 <= grid[i].length <= 50-1000 <= grid[i][j] <= 10000 <= k <= 100
Solution 1: Simulation
Simulate the shift process for k times.
Time complexity: O(k*n*m)
Space complexity: O(1) in-place
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
// Author: Huahua, 80ms, 13.5 MB class Solution { public: vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) { const int n = grid.size(); const int m = grid[0].size(); while (k--) { int last = grid[n - 1][m - 1]; for (int i = n - 1; i >= 0; --i) for (int j = m - 1; j >= 0; --j) { if (i == 0 && j == 0) grid[i][j] = last; else if (j == 0) grid[i][j] = grid[i - 1][m - 1]; else grid[i][j] = grid[i][j - 1]; } } return grid; } }; |
Solution 2: Rotate
Shift k times is equivalent to flatten the matrix and rotate by -k or (m*n – k % (m * n)).
Time complexity: O(m*n)
Space complexity: O(m*n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// Author: Huahua, 68 ms, 14.4 MB class Solution { public: vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) { const int n = grid.size(); const int m = grid[0].size(); k = m * n - k % (m*n); vector<int> g; for (int i = 0; i < n; ++i) g.insert(end(g), begin(grid[i]), end(grid[i])); rotate(begin(g), begin(g) + k, end(g)); auto it = begin(g); for (int i = 0; i < n; ++i) for (int j = 0; j < m; ++j) grid[i][j] = *it++; return grid; } }; |
O(1) space in-place rotation
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
// Author: Huahua, 68 ms, 13.6 MB class MatrixIterator { public: MatrixIterator(vector<vector<int>>& data, int index = 0) : data_(data), index_(index) {} MatrixIterator& operator++() { ++index_; return *this; } MatrixIterator& operator--() { --index_; return *this; } MatrixIterator operator +(int dis) const { return MatrixIterator(data_, index_ + dis); } MatrixIterator operator -(int dis) const { return MatrixIterator(data_, index_ - dis); } bool operator==(const MatrixIterator& o) const { return data_ == o.data_ && index_ == o.index_; } bool operator!=(const MatrixIterator& o) const { return data_ != o.data_ || index_ != o.index_; } ptrdiff_t operator-(const MatrixIterator& o) const { return index_ - o.index_; } MatrixIterator& operator=(const MatrixIterator& o) { data_ = o.data_; index_ = o.index_; return *this; } int& operator*() { if (index_ <= 0) { return data_[0][0]; } else if (index_ >= m() * n()) { return data_.back().back(); } else { return data_[index_ / m()][index_ % m()]; } } private: int n() const { return data_.size(); } int m() const { return n() == 0 ? 0 : data_[0].size(); } vector<vector<int>>& data_; int index_; }; namespace std { template<> struct iterator_traits<MatrixIterator> { typedef ptrdiff_t difference_type; typedef int value_type; typedef int* pointer; typedef int& reference; typedef random_access_iterator_tag iterator_category; }; } class Solution { public: vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) { const int n = grid.size(); const int m = grid[0].size(); k = m * n - k % (m*n); MatrixIterator it(grid); rotate(it, it + k, it + m * n); return grid; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment