花花酱 LeetCode 1261. Find Elements in a Contaminated Binary Tree

Given a binary tree with the following rules:

1. root.val == 0
2. If treeNode.val == x and treeNode.left != null, then treeNode.left.val == 2 * x + 1
3. If treeNode.val == x and treeNode.right != null, then treeNode.right.val == 2 * x + 2

Now the binary tree is contaminated, which means all treeNode.val have been changed to -1.

You need to first recover the binary tree and then implement the FindElements class:

• FindElements(TreeNode* root) Initializes the object with a contamined binary tree, you need to recover it first.
• bool find(int target) Return if the target value exists in the recovered binary tree.

Example 1:

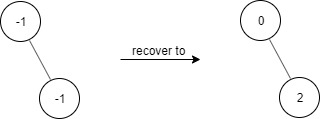
Input
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
Output

[null,false,true]

Explanation FindElements findElements = new FindElements([-1,null,-1]); findElements.find(1); // return False findElements.find(2); // return True

Example 2:

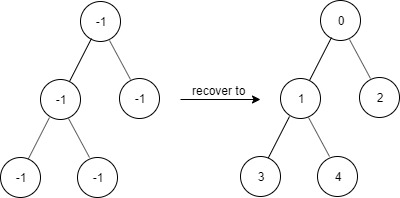
Input
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
Output

[null,true,true,false]

Explanation FindElements findElements = new FindElements([-1,-1,-1,-1,-1]); findElements.find(1); // return True findElements.find(3); // return True findElements.find(5); // return False

Example 3:

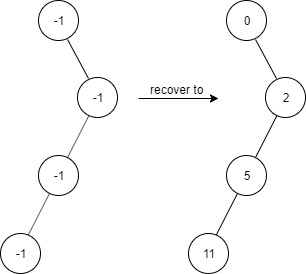
Input
["FindElements","find","find","find","find"]
[[[-1,null,-1,-1,null,-1]],[2],[3],[4],[5]]
Output

[null,true,false,false,true]

Explanation FindElements findElements = new FindElements([-1,null,-1,-1,null,-1]); findElements.find(2); // return True findElements.find(3); // return False findElements.find(4); // return False findElements.find(5); // return True

Constraints:

• TreeNode.val == -1
• The height of the binary tree is less than or equal to 20
• The total number of nodes is between [1, 10^4]
• Total calls of find() is between [1, 10^4]
• 0 <= target <= 10^6

Solutoin 1: Recursion and HashSet

Time complexity: Recover O(n), find O(1)
Space complexity: O(n)

Solution 2: Recursion and Binary format

The binary format of t = (target + 1) (from high bit to low bit, e.g. in reverse order) decides where to go at each node.
t % 2 == 1, go right, otherwise go left
t = t / 2 or t >>= 1

Time complexity: Recover O(n), find O(log|target|)
Space complexity: O(1)