Posts tagged as “greedy”

花花酱 LeetCode 1792. Maximum Average Pass Ratio

By zxi on March 13, 2021

There is a school that has classes of students and each class will be having a final exam. You are given a 2D integer array classes, where classes[i] = [pass_i, total_i]. You know beforehand that in the i^th class, there are total_i total students, but only pass_i number of students will pass the exam.

You are also given an integer extraStudents. There are another extraStudents brilliant students that are guaranteed to pass the exam of any class they are assigned to. You want to assign each of the extraStudents students to a class in a way that maximizes the average pass ratio across all the classes.

The pass ratio of a class is equal to the number of students of the class that will pass the exam divided by the total number of students of the class. The average pass ratio is the sum of pass ratios of all the classes divided by the number of the classes.

Return the maximum possible average pass ratio after assigning the extraStudents students. Answers within 10^-5 of the actual answer will be accepted.

Example 1:

Input: classes = [[1,2],[3,5],[2,2]], extraStudents = 2
Output: 0.78333
Explanation: You can assign the two extra students to the first class. The average pass ratio will be equal to (3/4 + 3/5 + 2/2) / 3 = 0.78333.

Example 2:

Input: classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4
Output: 0.53485

Constraints:

1 <= classes.length <= 10⁵
classes[i].length == 2
1 <= pass_i <= total_i <= 10⁵
1 <= extraStudents <= 10⁵

Solution: Greedy + Heap

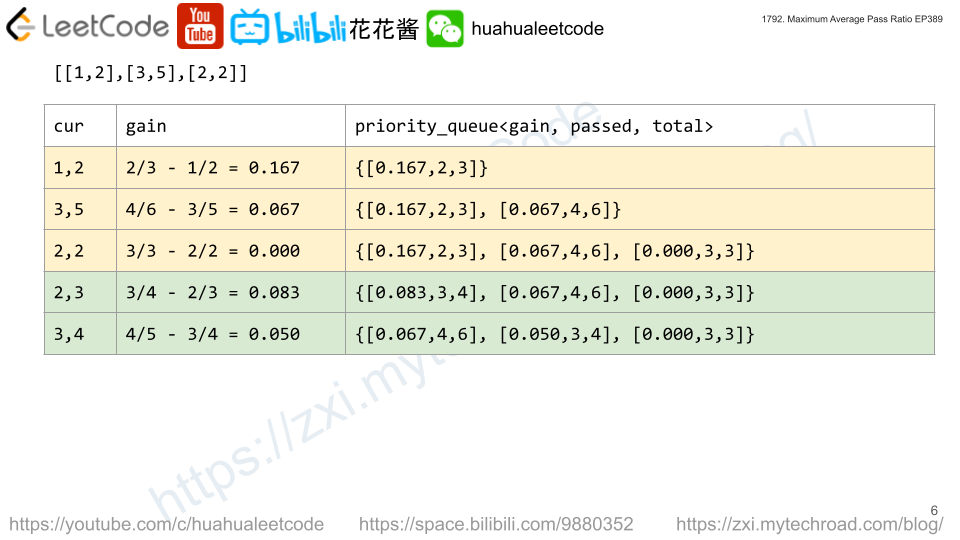
Sort by the ratio increase potential (p + 1) / (t + 1) – p / t.

Time complexity: O((m+n)logn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {

const int n = classes.size();

auto ratio = [&](int i, int delta = 0) {

return static_cast<double>(classes[i][0] + delta) /

(classes[i][1] + delta);

};

priority_queue<pair<double, int>> q;

for (int i = 0; i < n; ++i)

q.emplace(ratio(i, 1) - ratio(i), i);

while (extraStudents--) {

const auto [r, i] = q.top(); q.pop();

++classes[i][0];

++classes[i][1];

q.emplace(ratio(i, 1) - ratio(i), i);

}

double total_ratio = 0;

for (int i = 0; i < n; ++i)

total_ratio += ratio(i);

return total_ratio / n;

}

};

Python3

# Author: Huahua

class Solution:

def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:

def ratio(i, delta=0):

return (classes[i][0] + delta) / (classes[i][1] + delta)

q = []

for i, c in enumerate(classes):

heapq.heappush(q, (-(ratio(i, 1) - ratio(i)), i))

for _ in range(extraStudents):

_, i = heapq.heappop(q)

classes[i][0] += 1

classes[i][1] += 1

heapq.heappush(q, (-(ratio(i, 1) - ratio(i)), i))

return mean(ratio(i) for i, _ in enumerate(classes))

花花酱 LeetCode 1780. Check if Number is a Sum of Powers of Three

By zxi on March 6, 2021

Given an integer n, return true if it is possible to represent n as the sum of distinct powers of three. Otherwise, return false.

An integer y is a power of three if there exists an integer x such that y == 3^x.

Example 1:

Input: n = 12
Output: true
Explanation: 12 = 3¹ + 3²

Example 2:

Input: n = 91
Output: true
Explanation: 91 = 3⁰ + 3² + 3⁴

Example 3:

Input: n = 21
Output: false

Constraints:

1 <= n <= 10⁷

Solution: Greedy + Math

Find the largest 3^x that <= n, subtract that from n and repeat the process.
x should be monotonically decreasing, otherwise we have duplicate terms.
e.g. 12 = 3² + 3¹ true
e.g. 21 = 3² + 3²+ 3¹ false

Time complexity: O(logn?)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool checkPowersOfThree(int n) {

int last = INT_MAX;

while (n) {

int p = 0;

int cur = 1;

while (cur * 3 <= n) {

cur *= 3;

++p;

}

if (p == last) return false;

last = p;

n -= cur;

}

return true;

}

};

花花酱 LeetCode 1775. Equal Sum Arrays With Minimum Number of Operations

By zxi on February 27, 2021

You are given two arrays of integers nums1 and nums2, possibly of different lengths. The values in the arrays are between 1 and 6, inclusive.

In one operation, you can change any integer’s value in any of the arrays to any value between 1 and 6, inclusive.

Return the minimum number of operations required to make the sum of values in nums1 equal to the sum of values in nums2. Return -1 if it is not possible to make the sum of the two arrays equal.

Example 1:

Input: nums1 = [1,2,3,4,5,6], nums2 = [1,1,2,2,2,2]
Output: 3
Explanation: You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed.
- Change nums2[0] to 6. nums1 = [1,2,3,4,5,6], nums2 = [6,1,2,2,2,2].
- Change nums1[5] to 1. nums1 = [1,2,3,4,5,1], nums2 = [6,1,2,2,2,2].
- Change nums1[2] to 2. nums1 = [1,2,2,4,5,1], nums2 = [6,1,2,2,2,2].

Example 2:

Input: nums1 = [1,1,1,1,1,1,1], nums2 = [6]
Output: -1
Explanation: There is no way to decrease the sum of nums1 or to increase the sum of nums2 to make them equal.

Example 3:

Input: nums1 = [6,6], nums2 = [1]
Output: 3
Explanation: You can make the sums of nums1 and nums2 equal with 3 operations. All indices are 0-indexed. 
- Change nums1[0] to 2. nums1 = [2,6], nums2 = [1].
- Change nums1[1] to 2. nums1 = [2,2], nums2 = [1].
- Change nums2[0] to 4. nums1 = [2,2], nums2 = [4].

Constraints:

1 <= nums1.length, nums2.length <= 10⁵
1 <= nums1[i], nums2[i] <= 6

Solution: Greedy

Assuming sum(nums1) < sum(nums2),
sort both arrays
* scan nums1 from left to right, we need to increase the value form the smallest one.
* scan nums2 from right to left, we need to decrease the value from the largest one.
Each time, select the one with the largest delta to change.

e.g. nums1[i] = 2, nums[j] = 4, delta1 = 6 – 2 = 4, delta2 = 4 – 1 = 3, Increase 2 to 6 instead of decreasing 4 to 1.

Time complexity: O(mlogm + nlogn)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minOperations(vector<int>& nums1, vector<int>& nums2) {

const int l1 = nums1.size();

const int l2 = nums2.size();

if (min(l1, l2) * 6 < max(l1, l2)) return -1;

int s1 = accumulate(begin(nums1), end(nums1), 0);

int s2 = accumulate(begin(nums2), end(nums2), 0);

if (s1 > s2) return minOperations(nums2, nums1);

sort(begin(nums1), end(nums1));

sort(begin(nums2), end(nums2));

int ans = 0;

int i = 0;

int j = l2 - 1;

while (s1 != s2) {

const int diff = s2 - s1;

if (j == l2 || (i != l1 && 6 - nums1[i] >= nums2[j] - 1)) {

const int x = min(6, nums1[i] + diff);

s1 += x - nums1[i++];

} else {

const int x = max(1, nums2[j] - diff);

s2 += x - nums2[j--];

}

++ans;

}

return ans;

}

};

花花酱 LeetCode 1754. Largest Merge Of Two Strings

By zxi on February 7, 2021

You are given two strings word1 and word2. You want to construct a string merge in the following way: while either word1 or word2 are non-empty, choose one of the following options:

If word1 is non-empty, append the first character in word1 to merge and delete it from word1.
- For example, if word1 = "abc" and merge = "dv", then after choosing this operation, word1 = "bc" and merge = "dva".
If word2 is non-empty, append the first character in word2 to merge and delete it from word2.
- For example, if word2 = "abc" and merge = "", then after choosing this operation, word2 = "bc" and merge = "a".

Return the lexicographically largest merge you can construct.

A string a is lexicographically larger than a string b (of the same length) if in the first position where a and b differ, a has a character strictly larger than the corresponding character in b. For example, "abcd" is lexicographically larger than "abcc" because the first position they differ is at the fourth character, and d is greater than c.

Example 1:

Input: word1 = "cabaa", word2 = "bcaaa"
Output: "cbcabaaaaa"
Explanation: One way to get the lexicographically largest merge is:
- Take from word1: merge = "c", word1 = "abaa", word2 = "bcaaa"
- Take from word2: merge = "cb", word1 = "abaa", word2 = "caaa"
- Take from word2: merge = "cbc", word1 = "abaa", word2 = "aaa"
- Take from word1: merge = "cbca", word1 = "baa", word2 = "aaa"
- Take from word1: merge = "cbcab", word1 = "aa", word2 = "aaa"
- Append the remaining 5 a's from word1 and word2 at the end of merge.

Example 2:

Input: word1 = "abcabc", word2 = "abdcaba"
Output: "abdcabcabcaba"

Constraints:

1 <= word1.length, word2.length <= 3000
word1 and word2 consist only of lowercase English letters.

Solution: Greedy

Always take a single char from the largest word. (NOT just the current char).

E.g.
ans = “”, w1 = “cabba”, w2 = “bcaaa”
w1 > w2, take from w1
ans = “c”, w1 = “abba”, w2 = “bcaaa”
w1 < w2, take from w2
ans = “cb”, w1 = “abba”, w2 = “caaa”
w1 < w2, take from w2
ans = “cbc”, w1 = “abba”, w2 = “aaa”
w1 > w2, take from w1. Note: both start with “a”, but we need to compare the entire word.
ans = “cbca”, w1 = “bba”, w2 = “aaa”
w1 > w2, take from w1
ans = “cbcab”, w1 = “ba”, w2 = “aaa”
…

Time complexity: O(min(m,n)^2)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

string largestMerge(string_view w1, string_view w2) {

string ans;

int m = w1.length(), n = w2.length();

int i = 0, j = 0;

while (i < m && j < n)

ans += w1.substr(i) > w2.substr(j) ? w1[i++] : w2[j++];

ans.append(w1.substr(i));

ans.append(w2.substr(j));

return ans;

}

};

花花酱 LeetCode 1753. Maximum Score From Removing Stones

By zxi on February 7, 2021

You are playing a solitaire game with three piles of stones of sizes a, b, and c respectively. Each turn you choose two different non-empty piles, take one stone from each, and add 1 point to your score. The game stops when there are fewer than two non-empty piles (meaning there are no more available moves).

Given three integers a, b, and c, return the maximum score you can get.

Example 1:

Input: a = 2, b = 4, c = 6
Output: 6
Explanation: The starting state is (2, 4, 6). One optimal set of moves is:
- Take from 1st and 3rd piles, state is now (1, 4, 5)
- Take from 1st and 3rd piles, state is now (0, 4, 4)
- Take from 2nd and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 6 points.

Example 2:

Input: a = 4, b = 4, c = 6
Output: 7
Explanation: The starting state is (4, 4, 6). One optimal set of moves is:
- Take from 1st and 2nd piles, state is now (3, 3, 6)
- Take from 1st and 3rd piles, state is now (2, 3, 5)
- Take from 1st and 3rd piles, state is now (1, 3, 4)
- Take from 1st and 3rd piles, state is now (0, 3, 3)
- Take from 2nd and 3rd piles, state is now (0, 2, 2)
- Take from 2nd and 3rd piles, state is now (0, 1, 1)
- Take from 2nd and 3rd piles, state is now (0, 0, 0)
There are fewer than two non-empty piles, so the game ends. Total: 7 points.

Example 3:

Input: a = 1, b = 8, c = 8
Output: 8
Explanation: One optimal set of moves is to take from the 2nd and 3rd piles for 8 turns until they are empty.
After that, there are fewer than two non-empty piles, so the game ends.

Constraints:

1 <= a, b, c <= 10⁵

Solution 1: Greedy

Take two stones (one each) from the largest two piles, until one is empty.

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

int maximumScore(int a, int b, int c) {

array<int, 3> s{a,b,c};

sort(begin(s), end(s));

int ans = 0;

while (s[1]-- && s[2]--) {

++ans;

sort(begin(s), end(s));

}

return ans;

}

};

Solution 2: Math

First, let’s assuming a <= b <= c.
There are two conditions:
1. a + b <= c, we can pair c with a first and then b. Total pairs is (a + b + (a + b)) / 2
2. a + b > c, we can pair c with a, b “evenly”, and then pair a with b, total pairs is (a + b + c) / 2

ans = (a + b + min(a + b, c)) / 2

Time complexity: O(1)
Space complexity: O(1)

C++

class Solution {

public:

int maximumScore(int a, int b, int c) {

array<int, 3> s{a,b,c};

sort(begin(s), end(s));

return (s[0] + s[1] + min(s[0] + s[1], s[2])) / 2;

}

};