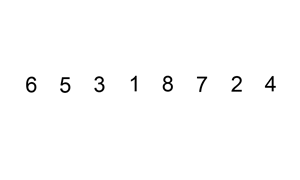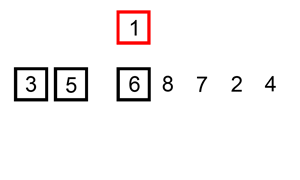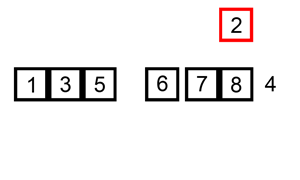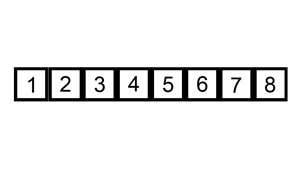You are given the head of a singly linked-list. The list can be represented as:
L0 → L1 → … → Ln - 1 → Ln
Reorder the list to be on the following form:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
You may not modify the values in the list’s nodes. Only nodes themselves may be changed.
Example 1:

Input: head = [1,2,3,4] Output: [1,4,2,3]
Example 2:

Input: head = [1,2,3,4,5] Output: [1,5,2,4,3]
Constraints:
- The number of nodes in the list is in the range
[1, 5 * 104]. 1 <= Node.val <= 1000
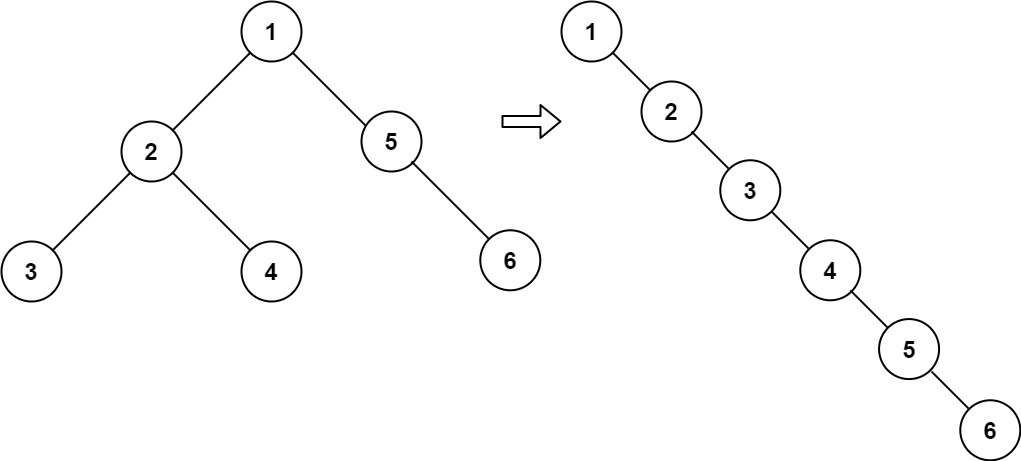
Solution: Three steps
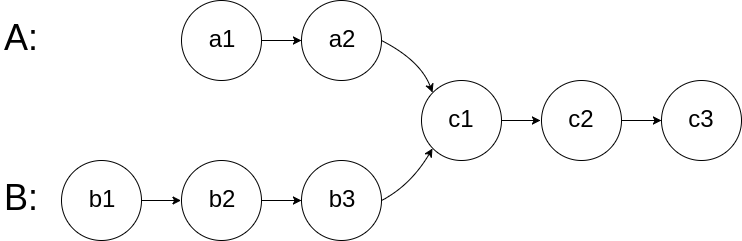
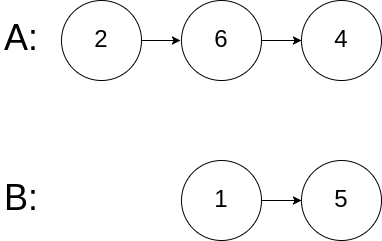
Step 1: Find mid node that splits the list into two halves.
Step 2: Reverse the second half
Step 3: Merge two lists
Time complexity: O(n)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
// Author: Huahua class Solution { public: void reorderList(ListNode* head) { if (!head || !head->next) return; ListNode* slow = head; ListNode* fast = head; while (fast->next && fast->next->next) { slow = slow->next; fast = fast->next->next; } ListNode* h1 = head; ListNode* h2 = reverse(slow->next); slow->next = nullptr; while (h1 && h2) { ListNode* n1 = h1->next; ListNode* n2 = h2->next; h1->next = h2; h2->next = n1; h1 = n1; h2 = n2; } } private: // reverse a linked list // returns head of the linked list ListNode* reverse(ListNode* head) { if (!head || !head->next) return head; ListNode* prev = head; ListNode* cur = head->next; ListNode* next = cur; while (cur) { next = next->next; cur->next = prev; prev = cur; cur = next; } head->next = nullptr; return prev; } }; |