Disjoint-set/Union-find Forest
Find(x): find the root/cluster-id of x
Union(x, y): merge two clusters
Check whether two elements are in the same set or not in O(1)*.
Find: O(ɑ(n))* ≈ O(1)
Union: O(ɑ(n))* ≈ O(1)
Space: O(n)
Without optimization: Find: O(n)
Two key optimizations:
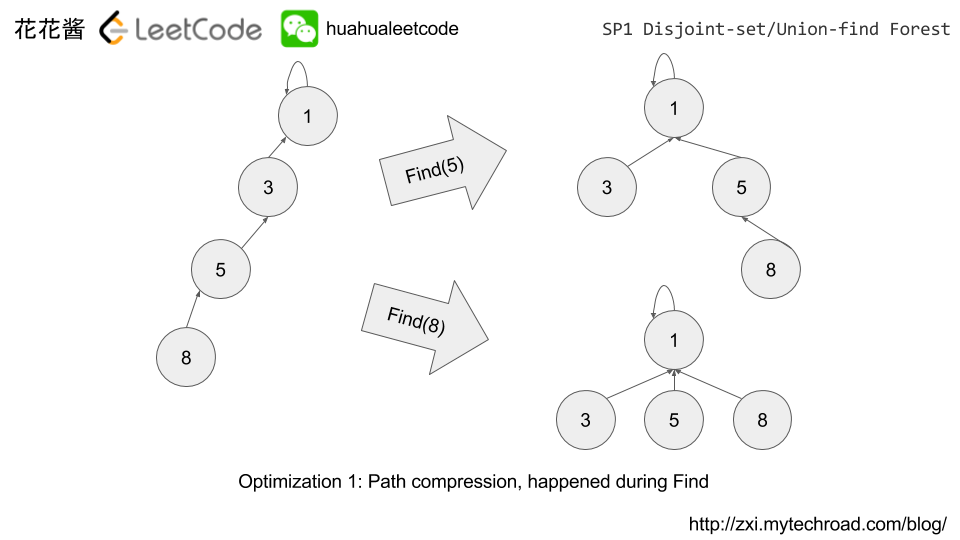
- Path compression: make tree flat
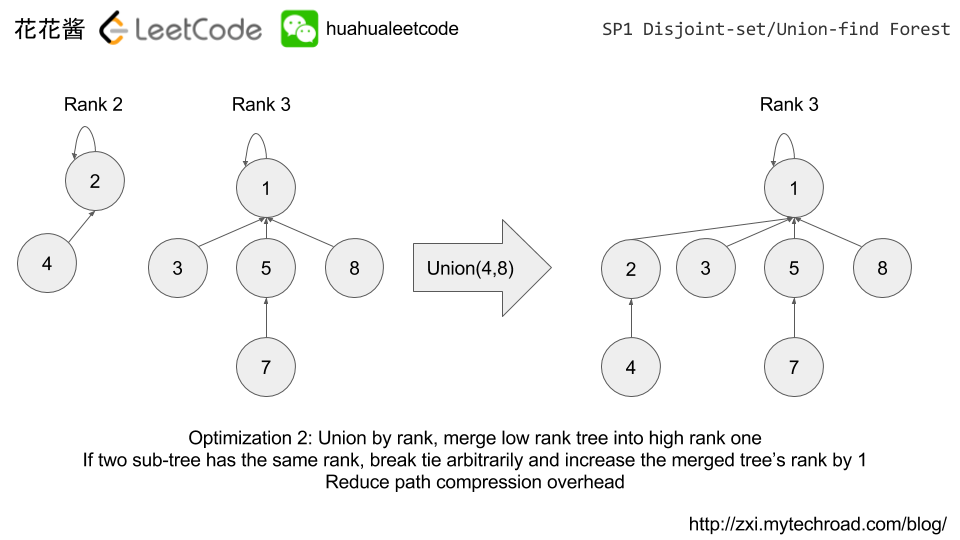
- Union by rank: merge low rank tree to high rank one
*: amortized
ɑ(.): inverse Ackermann function
Implementations:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
// Author: Huahua class UnionFindSet { public: UnionFindSet(int n) { ranks_ = vector<int>(n + 1, 0); parents_ = vector<int>(n + 1, 0); for (int i = 0; i < parents_.size(); ++i) parents_[i] = i; } // Merge sets that contains u and v. // Return true if merged, false if u and v are already in one set. bool Union(int u, int v) { int pu = Find(u); int pv = Find(v); if (pu == pv) return false; // Meger low rank tree into high rank tree if (ranks_[pv] < ranks_[pu]) parents_[pv] = pu; else if (ranks_[pu] < ranks_[pv]) parents_[pu] = pv; else { parents_[pv] = pu; ranks_[pu] += 1; } return true; } // Get the root of u. int Find(int u) { // Compress the path during traversal if (u != parents_[u]) parents_[u] = Find(parents_[u]); return parents_[u]; } private: vector<int> parents_; vector<int> ranks_; }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
// Author: Huahua class UnionFindSet { private int[] parents_; private int[] ranks_; public UnionFindSet(int n) { parents_ = new int[n + 1]; ranks_ = new int[n + 1]; for (int i = 0; i < parents_.length; ++i) { parents_[i] = i; ranks_[i] = 1; } } public boolean Union(int u, int v) { int pu = Find(u); int pv = Find(v); if (pu == pv) return false; if (ranks_[pv] > ranks_[pu]) parents_[pu] = pv; else if (ranks_[pu] > ranks_[pv]) parents_[pv] = pu; else { parents_[pv] = pu; ranks_[pu] += 1; } return true; } public int Find(int u) { while (parents_[u] != u) { parents_[u] = parents_[parents_[u]]; u = parents_[u]; } return u; } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
""" Author: Huahua """ class UnionFindSet: def __init__(self, n): self._parents = [i for i in range(n + 1)] self._ranks = [1 for i in range(n + 1)] def find(self, u): while u != self._parents[u]: self._parents[u] = self._parents[self._parents[u]] u = self._parents[u] return u def union(self, u, v): pu, pv = self.find(u), self.find(v) if pu == pv: return False if self._ranks[pu] < self._ranks[pv]: self._parents[pu] = pv elif self._ranks[pu] > self._ranks[pv]: self._parents[pv] = pu else: self._parents[pv] = pu self._ranks[pu] += 1 return True |
Union-Find Problems
- 花花酱 LeetCode 399. Evaluate Division
- 花花酱 LeetCode 547. Friend Circles
- 花花酱 LeetCode 737. Sentence Similarity II
- 花花酱 LeetCode 684. Redundant Connection
- 花花酱 LeetCode 685. Redundant Connection II
- 花花酱 LeetCode 839. Similar String Groups
References
请尊重作者的劳动成果，转载请注明出处！花花保留对文章／视频的所有权利。
如果您喜欢这篇文章／视频，欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.
Paypal
Venmo
huahualeetcode
huahualeetcode
微信打赏
Be First to Comment