You are given two strings, word1 and word2. You want to construct a string in the following manner:
- Choose some non-empty subsequence
subsequence1fromword1. - Choose some non-empty subsequence
subsequence2fromword2. - Concatenate the subsequences:
subsequence1 + subsequence2, to make the string.
Return the length of the longest palindrome that can be constructed in the described manner. If no palindromes can be constructed, return 0.
A subsequence of a string s is a string that can be made by deleting some (possibly none) characters from s without changing the order of the remaining characters.
A palindrome is a string that reads the same forward as well as backward.
Example 1:
Input: word1 = "cacb", word2 = "cbba" Output: 5 Explanation: Choose "ab" from word1 and "cba" from word2 to make "abcba", which is a palindrome.
Example 2:
Input: word1 = "ab", word2 = "ab" Output: 3 Explanation: Choose "ab" from word1 and "a" from word2 to make "aba", which is a palindrome.
Example 3:
Input: word1 = "aa", word2 = "bb" Output: 0 Explanation: You cannot construct a palindrome from the described method, so return 0.
Constraints:
1 <= word1.length, word2.length <= 1000word1andword2consist of lowercase English letters.
Solution: DP

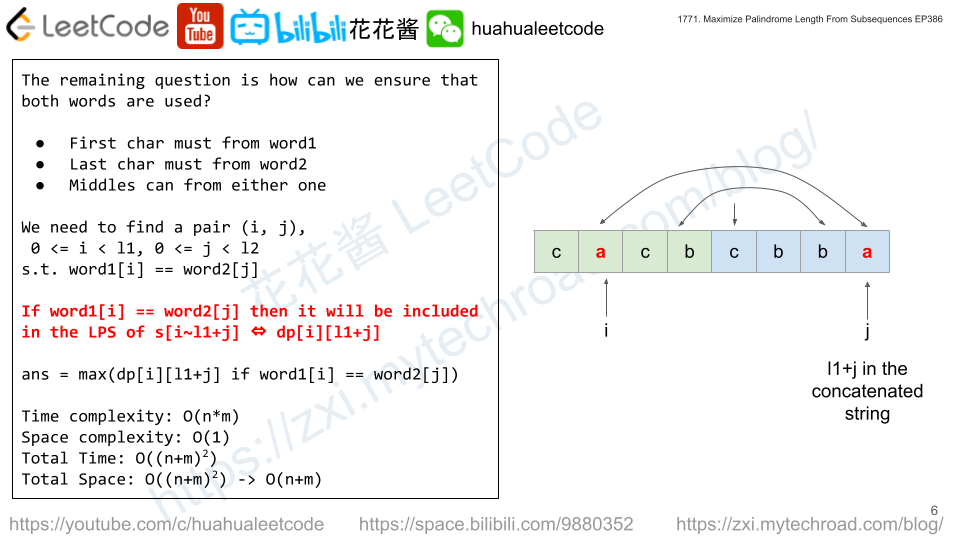
Similar to 花花酱 LeetCode 516. Longest Palindromic Subsequence
Let s = word1 + word2, build dp table on s. We just need to make sure there’s at least one char from each string.
Time complexity: O((m+n)^2)
Space complexity: O((m+n)^2)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
// Author: Huahua class Solution { public: int longestPalindrome(string word1, string word2) { const int l1 = word1.length(); const int l2 = word2.length(); string s = word1 + word2; const int n = l1 + l2; vector<vector<int>> dp(n, vector<int>(n)); for (int i = 0; i < n; ++i) dp[i][i] = 1; for (int l = 2; l <= n; ++l) for (int i = 0, j = i + l - 1; j < n; ++i, ++j) { if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2; else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); } int ans = 0; for (int i = 0; i < l1; ++i) for (int j = 0; j < l2; ++j) if (word1[i] == word2[j]) ans = max(ans, dp[i][l1 + j]); return ans; } }; |
O(m+n) Space complexity
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
// Author: Huahua class Solution { public: int longestPalindrome(string word1, string word2) { const int l1 = word1.length(); const int l2 = word2.length(); string s = word1 + word2; const int n = l1 + l2; vector<int> dp1(n, 1), dp2(n); int ans = 0; for (int l = 2; l <= n; ++l) { vector<int> dp(n); for (int i = 0, j = i + l - 1; j < n; ++i, ++j) { if (s[i] == s[j]) { dp[i] = dp2[i + 1] + 2; if (i < l1 && j >= l1) ans = max(ans, dp[i]); } else { dp[i] = max(dp1[i + 1], dp1[i]); } } // dp2, dp1 = dp1, dp dp1.swap(dp); dp2.swap(dp); } return ans; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment