Huahua’s Tech Road

花花酱 LeetCode 1573. Number of Ways to Split a String

By zxi on September 5, 2020

Given a binary string s (a string consisting only of ‘0’s and ‘1’s), we can split s into 3 non-empty strings s1, s2, s3 (s1+ s2+ s3 = s).

Return the number of ways s can be split such that the number of characters ‘1’ is the same in s1, s2, and s3.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: s = "10101"
Output: 4
Explanation: There are four ways to split s in 3 parts where each part contain the same number of letters '1'.
"1|010|1"
"1|01|01"
"10|10|1"
"10|1|01"

Example 2:

Input: s = "1001"
Output: 0

Example 3:

Input: s = "0000"
Output: 3
Explanation: There are three ways to split s in 3 parts.
"0|0|00"
"0|00|0"
"00|0|0"

Example 4:

Input: s = "100100010100110"
Output: 12

Constraints:

s[i] == '0' or s[i] == '1'
3 <= s.length <= 10^5

Solution: Counting

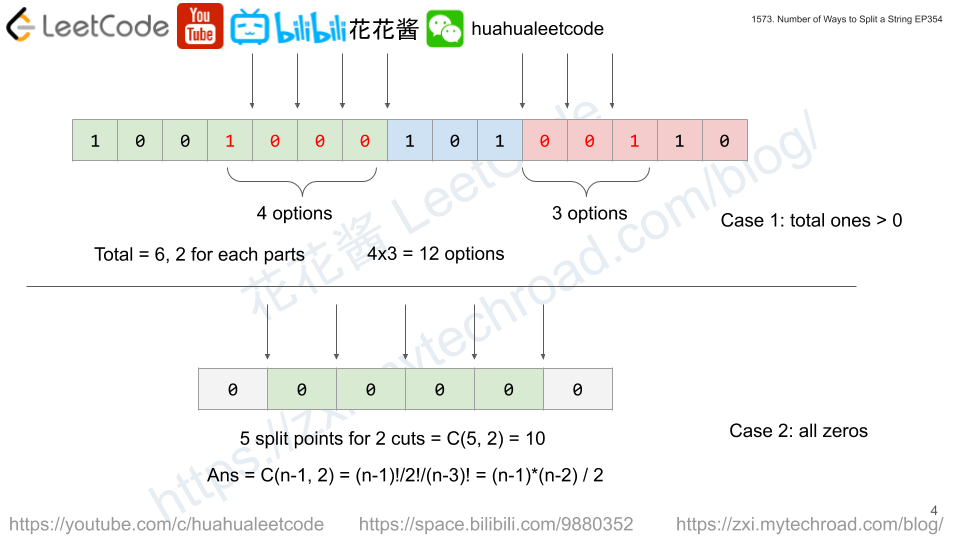
Count how many ones in the binary string as T, if not a factor of 3, then there is no answer.

Count how many positions that have prefix sum of T/3 as l, and how many positions that have prefix sum of T/3*2 as r.

Ans = l * r

But we need to special handle the all zero cases, which equals to C(n-2, 2) = (n – 1) * (n – 2) / 2

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

int numWays(string s) {

const int kMod = 1e9 + 7;

const long n = s.length();

int t = 0;

for (char c : s) t += c == '1';

if (t % 3) return 0;

if (t == 0)

return ((1 + (n - 2)) * (n - 2) / 2) % kMod;

t /= 3;

long l = 0;

long r = 0;

for (int i = 0, c = 0; i < n; ++i) {

c += (s[i] == '1');

if (c == t) ++l;

else if (c == t * 2) ++r;

}

return (l * r) % kMod;

}

};

Python3

class Solution:

def numWays(self, s: str) -> int:

n = len(s)

t = s.count('1')

if t % 3 != 0: return 0

if t == 0: return ((n - 1) * (n - 2) // 2) % (10**9 + 7)

t //= 3

l, r, c = 0, 0, 0

for i, ch in enumerate(s):

if ch == '1': c += 1

if c == t: l += 1

elif c == t * 2: r += 1

return (l * r) % (10**9 + 7)

One pass: Space complexity: O(n)

Python3

class Solution:

def numWays(self, s: str) -> int:

n = len(s)

p = defaultdict(int)

c = 0

for ch in s:

if ch == '1': c += 1

p[c] += 1

if c % 3 != 0: return 0

if c == 0: return ((n - 1) * (n - 2) // 2) % (10**9 + 7)

return (p[c // 3] * p[c // 3 * 2]) % (10**9 + 7)

花花酱 LeetCode 1572. Matrix Diagonal Sum

By zxi on September 5, 2020

Given a square matrix mat, return the sum of the matrix diagonals.

Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.

Example 1:

Input: mat = [[1,2,3],
              [4,5,6],
              [7,8,9]]
Output: 25
Explanation: Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat[1][1] = 5 is counted only once.

Example 2:

Input: mat = [[1,1,1,1],
              [1,1,1,1],
              [1,1,1,1],
              [1,1,1,1]]
Output: 8

Example 3:

Input: mat = [[5]]
Output: 5

Constraints:

n == mat.length == mat[i].length
1 <= n <= 100
1 <= mat[i][j] <= 100

Solution: Brute Force

Note: if n is odd, be careful not to double count the center one.

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

int diagonalSum(vector<vector<int>>& mat) {

const int n = mat.size();

int ans = 0;

for (int i = 0; i < n; ++i)

ans += mat[i][i] + mat[i][n - i - 1];

if (n & 1) ans -= mat[n / 2][n / 2];

return ans;

}

};

花花酱 LeetCode 1569. Number of Ways to Reorder Array to Get Same BST

By zxi on August 30, 2020

Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.

For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.

Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.

Since the answer may be very large, return it modulo 10^9 + 7.

Example 1:

Input: nums = [2,1,3]
Output: 1
Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.

Example 2:

Input: nums = [3,4,5,1,2]
Output: 5
Explanation: The following 5 arrays will yield the same BST: 
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

Example 3:

Input: nums = [1,2,3]
Output: 0
Explanation: There are no other orderings of nums that will yield the same BST.

Example 4:

Input: nums = [3,1,2,5,4,6]
Output: 19

Example 5:

Input: nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18]
Output: 216212978
Explanation: The number of ways to reorder nums to get the same BST is 3216212999. Taking this number modulo 10^9 + 7 gives 216212978.

Constraints:

1 <= nums.length <= 1000
1 <= nums[i] <= nums.length
All integers in nums are distinct.

Solution: Recursion + Combinatorics

For a given root (first element of the array), we can split the array into left children (nums[i] < nums[0]) and right children (nums[i] > nums[0]). Assuming there are l nodes for the left and r nodes for the right. We have C(l + r, l) different ways to insert l elements into a (l + r) sized array. Within node l / r nodes, we have ways(left) / ways(right) different ways to re-arrange those nodes. So the total # of ways is:
C(l + r, l) * ways(l) * ways(r)
Don’t forget to minus one for the final answer.

Time complexity: O(n^2)
Space complexity: O(n^2)

C++

class Solution {

public:

int numOfWays(vector<int>& nums) {

const int n = nums.size();

const int kMod = 1e9 + 7;

vector<vector<int>> cnk(n + 1, vector<int>(n + 1, 1));

for (int i = 1; i <= n; ++i)

for (int j = 1; j < i; ++j)

cnk[i][j] = (cnk[i - 1][j] + cnk[i - 1][j - 1]) % kMod;

function<int(vector<int>)> trees = [&](const vector<int>& nums) {

const int n = nums.size();

if (n <= 2) return 1;

vector<int> left;

vector<int> right;

for (int i = 1; i < nums.size(); ++i)

if (nums[i] < nums[0]) left.push_back(nums[i]);

else right.push_back(nums[i]);

long ans = cnk[n - 1][left.size()];

ans = (ans * trees(left)) % kMod;

ans = (ans * trees(right)) % kMod;

return static_cast<int>(ans);

};

return trees(nums) - 1;

}

};

python3

class Solution:

def numOfWays(self, nums: List[int]) -> int:

def ways(nums):

if len(nums) <= 2: return 1

l = [x for x in nums if x < nums[0]]

r = [x for x in nums if x > nums[0]]

return comb(len(l) + len(r), len(l)) * ways(l) * ways(r)

return (ways(nums) - 1) % (10**9 + 7)

花花酱 LeetCode 1568. Minimum Number of Days to Disconnect Island

By zxi on August 30, 2020

Given a 2D grid consisting of 1s (land) and 0s (water). An island is a maximal 4-directionally (horizontal or vertical) connected group of 1s.

The grid is said to be connected if we have exactly one island, otherwise is said disconnected.

In one day, we are allowed to change any single land cell (1) into a water cell (0).

Return the minimum number of days to disconnect the grid.

Example 1:

Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
Output: 2
Explanation: We need at least 2 days to get a disconnected grid.
Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.

Example 2:

Input: grid = [[1,1]]
Output: 2
Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.

Example 3:

Input: grid = [[1,0,1,0]]
Output: 0

Example 4:

Input: grid = [[1,1,0,1,1],
               [1,1,1,1,1],
               [1,1,0,1,1],
               [1,1,0,1,1]]
Output: 1

Example 5:

Input: grid = [[1,1,0,1,1],
               [1,1,1,1,1],
               [1,1,0,1,1],
               [1,1,1,1,1]]
Output: 2

Constraints:

1 <= grid.length, grid[i].length <= 30
grid[i][j] is 0 or 1.

Solution: Brute Force

We need at most two days to disconnect an island.
1. check if we have more than one islands. (0 days)
2. For each 1 cell, change it to 0 and check how many islands do we have. (1 days)
3. Otherwise, 2 days

Time complexity: O(m^2*n^2)
Space complexity: O(m*n)

C++

class Solution {

public:

int minDays(vector<vector<int>>& grid) {

const int n = grid.size();

const int m = grid[0].size();

const vector<int> dirs{0, 1, 0, -1, 0};

vector<int> seen(n * m);

function<void(int, int)> dfs = [&](int x, int y) {

if (x < 0 || y < 0 || x >= m || y >= n) return;

if (grid[y][x] == 0) return;

if (seen[y * m + x]++) return;

for (int i = 0; i < 4; ++i)

dfs(x + dirs[i], y + dirs[i + 1]);

};

function<bool()> disconnected = [&]() {

int count = 0;

fill(begin(seen), end(seen), 0);

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x)

if (grid[y][x] && !seen[y * m + x]) {

dfs(x, y);

if (++count > 1) return true;

}

return false;

};

if (disconnected()) return 0;

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x) {

if (!grid[y][x]) continue;

grid[y][x] = 0;

if (disconnected()) return 1;

grid[y][x] = 1;

}

return 2;

}

};

花花酱 LeetCode 1567. Maximum Length of Subarray With Positive Product

By zxi on August 29, 2020

Given an array of integers nums, find the maximum length of a subarray where the product of all its elements is positive.

A subarray of an array is a consecutive sequence of zero or more values taken out of that array.

Return the maximum length of a subarray with positive product.

Example 1:

Input: nums = [1,-2,-3,4]
Output: 4
Explanation: The array nums already has a positive product of 24.

Example 2:

Input: nums = [0,1,-2,-3,-4]
Output: 3
Explanation: The longest subarray with positive product is [1,-2,-3] which has a product of 6.
Notice that we cannot include 0 in the subarray since that'll make the product 0 which is not positive.

Example 3:

Input: nums = [-1,-2,-3,0,1]
Output: 2
Explanation: The longest subarray with positive product is [-1,-2] or [-2,-3].

Example 4:

Input: nums = [-1,2]
Output: 1

Example 5:

Input: nums = [1,2,3,5,-6,4,0,10]
Output: 4

Constraints:

1 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9

Solution: DP

p[i] := max length of positive products ends with arr[i]
n[i] := max length of negtive products ends with arr[i]

if arr[i] > 0: p[i] = p[i – 1] + 1, n[i] = n[i] + 1 if n[i] else 0
if arr[i] < 0: p[i] = n[i – 1] + 1 if n[i – 1] else 0, n[i] = p[i – 1] + 1
if arr[i] == 0: p[i] = n[i] = 0
ans = max(p[i])

Time complexity: O(n)
Space complexity: O(n) -> O(1)

C++

class Solution {

public:

int getMaxLen(vector<int>& nums) {

int p = 0;

int n = 0;

int ans = 0;

for (int x : nums) {

if (x > 0) {

++p;

if (n) ++n;

} else if (x < 0) {

int tp = p;

p = n ? n + 1 : 0;

n = tp + 1;

} else {

p = n = 0;

}

ans = max(ans, p);

}

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1573. Number of Ways to Split a String

Solution: Counting

C++

Python3

Python3

花花酱 LeetCode 1572. Matrix Diagonal Sum

Solution: Brute Force

C++

花花酱 LeetCode 1569. Number of Ways to Reorder Array to Get Same BST

Solution: Recursion + Combinatorics

C++

python3

花花酱 LeetCode 1568. Minimum Number of Days to Disconnect Island

Solution: Brute Force

C++

花花酱 LeetCode 1567. Maximum Length of Subarray With Positive Product

Solution: DP

C++