Huahua’s Tech Road

花花酱 LeetCode 1568. Minimum Number of Days to Disconnect Island

By zxi on August 30, 2020

Given a 2D grid consisting of 1s (land) and 0s (water). An island is a maximal 4-directionally (horizontal or vertical) connected group of 1s.

The grid is said to be connected if we have exactly one island, otherwise is said disconnected.

In one day, we are allowed to change any single land cell (1) into a water cell (0).

Return the minimum number of days to disconnect the grid.

Example 1:

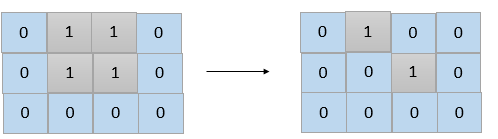
Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
Output: 2
Explanation: We need at least 2 days to get a disconnected grid.
Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.

Example 2:

Input: grid = [[1,1]]
Output: 2
Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.

Example 3:

Input: grid = [[1,0,1,0]]
Output: 0

Example 4:

Input: grid = [[1,1,0,1,1],
               [1,1,1,1,1],
               [1,1,0,1,1],
               [1,1,0,1,1]]
Output: 1

Example 5:

Input: grid = [[1,1,0,1,1],
               [1,1,1,1,1],
               [1,1,0,1,1],
               [1,1,1,1,1]]
Output: 2

Constraints:

1 <= grid.length, grid[i].length <= 30
grid[i][j] is 0 or 1.

Solution: Brute Force

We need at most two days to disconnect an island.
1. check if we have more than one islands. (0 days)
2. For each 1 cell, change it to 0 and check how many islands do we have. (1 days)
3. Otherwise, 2 days

Time complexity: O(m^2*n^2)
Space complexity: O(m*n)

C++

class Solution {

public:

int minDays(vector<vector<int>>& grid) {

const int n = grid.size();

const int m = grid[0].size();

const vector<int> dirs{0, 1, 0, -1, 0};

vector<int> seen(n * m);

function<void(int, int)> dfs = [&](int x, int y) {

if (x < 0 || y < 0 || x >= m || y >= n) return;

if (grid[y][x] == 0) return;

if (seen[y * m + x]++) return;

for (int i = 0; i < 4; ++i)

dfs(x + dirs[i], y + dirs[i + 1]);

};

function<bool()> disconnected = [&]() {

int count = 0;

fill(begin(seen), end(seen), 0);

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x)

if (grid[y][x] && !seen[y * m + x]) {

dfs(x, y);

if (++count > 1) return true;

}

return false;

};

if (disconnected()) return 0;

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x) {

if (!grid[y][x]) continue;

grid[y][x] = 0;

if (disconnected()) return 1;

grid[y][x] = 1;

}

return 2;

}

};

花花酱 LeetCode 1567. Maximum Length of Subarray With Positive Product

By zxi on August 29, 2020

Given an array of integers nums, find the maximum length of a subarray where the product of all its elements is positive.

A subarray of an array is a consecutive sequence of zero or more values taken out of that array.

Return the maximum length of a subarray with positive product.

Example 1:

Input: nums = [1,-2,-3,4]
Output: 4
Explanation: The array nums already has a positive product of 24.

Example 2:

Input: nums = [0,1,-2,-3,-4]
Output: 3
Explanation: The longest subarray with positive product is [1,-2,-3] which has a product of 6.
Notice that we cannot include 0 in the subarray since that'll make the product 0 which is not positive.

Example 3:

Input: nums = [-1,-2,-3,0,1]
Output: 2
Explanation: The longest subarray with positive product is [-1,-2] or [-2,-3].

Example 4:

Input: nums = [-1,2]
Output: 1

Example 5:

Input: nums = [1,2,3,5,-6,4,0,10]
Output: 4

Constraints:

1 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9

Solution: DP

p[i] := max length of positive products ends with arr[i]
n[i] := max length of negtive products ends with arr[i]

if arr[i] > 0: p[i] = p[i – 1] + 1, n[i] = n[i] + 1 if n[i] else 0
if arr[i] < 0: p[i] = n[i – 1] + 1 if n[i – 1] else 0, n[i] = p[i – 1] + 1
if arr[i] == 0: p[i] = n[i] = 0
ans = max(p[i])

Time complexity: O(n)
Space complexity: O(n) -> O(1)

C++

class Solution {

public:

int getMaxLen(vector<int>& nums) {

int p = 0;

int n = 0;

int ans = 0;

for (int x : nums) {

if (x > 0) {

++p;

if (n) ++n;

} else if (x < 0) {

int tp = p;

p = n ? n + 1 : 0;

n = tp + 1;

} else {

p = n = 0;

}

ans = max(ans, p);

}

return ans;

}

};

花花酱 LeetCode 1566. Detect Pattern of Length M Repeated K or More Times

By zxi on August 29, 2020

Given an array of positive integers arr, find a pattern of length m that is repeated k or more times.

A pattern is a subarray (consecutive sub-sequence) that consists of one or more values, repeated multiple times consecutively without overlapping. A pattern is defined by its length and the number of repetitions.

Return true if there exists a pattern of length m that is repeated k or more times, otherwise return false.

Example 1:

Input: arr = [1,2,4,4,4,4], m = 1, k = 3
Output: true
Explanation: The pattern (4) of length 1 is repeated 4 consecutive times. Notice that pattern can be repeated k or more times but not less.

Example 2:

Input: arr = [1,2,1,2,1,1,1,3], m = 2, k = 2
Output: true
Explanation: The pattern (1,2) of length 2 is repeated 2 consecutive times. Another valid pattern (2,1) is also repeated 2 times.

Example 3:

Input: arr = [1,2,1,2,1,3], m = 2, k = 3
Output: false
Explanation: The pattern (1,2) is of length 2 but is repeated only 2 times. There is no pattern of length 2 that is repeated 3 or more times.

Example 4:

Input: arr = [1,2,3,1,2], m = 2, k = 2
Output: false
Explanation: Notice that the pattern (1,2) exists twice but not consecutively, so it doesn't count.

Example 5:

Input: arr = [2,2,2,2], m = 2, k = 3
Output: false
Explanation: The only pattern of length 2 is (2,2) however it's repeated only twice. Notice that we do not count overlapping repetitions.

Constraints:

2 <= arr.length <= 100
1 <= arr[i] <= 100
1 <= m <= 100
2 <= k <= 100

Solution 1: Brute Force

Time complexity: O(nmk)
Space complexity: O(1)

C++

class Solution {

public:

bool containsPattern(vector<int>& arr, int m, int k) {

const int n = arr.size();

for (int i = 0; i + m * k <= n; ++i) {

bool valid = true;

for (int j = 1; j < k && valid; ++j)

for (int p = 0; p < m && valid; ++p)

if (arr[i + j * m + p] != arr[i + p])

valid = false;

if (valid) return true;

}

return false;

}

};

Solution 2: Shift and count

Since we need k consecutive subarrays, we can compare arr[i] with arr[i + m], if they are the same, increase the counter, otherwise reset the counter. If the counter reaches (k – 1) * m, it means we found k consecutive subarrays of length m.

ex1: arr = [1,2,4,4,4,4], m = 1, k = 3
i arr[i], arr[i + m] counter
0 1. 2. 0
0 2. 4. 0
0 4. 4. 1
0 4. 4. 2. <– found

ex2: arr = [1,2,1,2,1,1,1,3], m = 2, k = 2
i arr[i], arr[i + m] counter
0 1. 1. 1
0 2. 2. 2 <– found

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

bool containsPattern(vector<int>& arr, int m, int k) {

const int n = arr.size();

int count = 0;

for (int i = 0; i + m < n; ++i) {

if (arr[i] == arr[i + m]) {

if (++count == (k - 1) * m) return true;

} else {

count = 0;

}

return false;

}

};

花花酱 LeetCode 1563. Stone Game V

By zxi on August 23, 2020

There are several stones arranged in a row, and each stone has an associated value which is an integer given in the array stoneValue.

In each round of the game, Alice divides the row into two non-empty rows (i.e. left row and right row), then Bob calculates the value of each row which is the sum of the values of all the stones in this row. Bob throws away the row which has the maximum value, and Alice’s score increases by the value of the remaining row. If the value of the two rows are equal, Bob lets Alice decide which row will be thrown away. The next round starts with the remaining row.

The game ends when there is only one stone remaining. Alice’s is initially zero.

Return the maximum score that Alice can obtain.

Example 1:

Input: stoneValue = [6,2,3,4,5,5]
Output: 18
Explanation: In the first round, Alice divides the row to [6,2,3], [4,5,5]. The left row has the value 11 and the right row has value 14. Bob throws away the right row and Alice's score is now 11.
In the second round Alice divides the row to [6], [2,3]. This time Bob throws away the left row and Alice's score becomes 16 (11 + 5).
The last round Alice has only one choice to divide the row which is [2], [3]. Bob throws away the right row and Alice's score is now 18 (16 + 2). The game ends because only one stone is remaining in the row.

Example 2:

Input: stoneValue = [7,7,7,7,7,7,7]
Output: 28

Example 3:

Input: stoneValue = [4]
Output: 0

Constraints:

1 <= stoneValue.length <= 500
1 <= stoneValue[i] <= 10^6

Solution: Range DP + Prefix Sum

dp[l][r] := max store Alice can get from range [l, r]
sum_l = sum(l, k), sum_r = sum(k + 1, r)
dp[l][r] = max{
dp[l][k] + sum_l if sum_l < sum_r
dp[k+1][r] + sum_r if sum_r < sum_l
max(dp[l][k], dp[k+1][r])) + sum_l if sum_l == sum_r)
} for k in [l, r)

Time complexity: O(n^3)
Space complexity: O(n^2)

C++

class Solution {

public:

int stoneGameV(vector<int>& stoneValue) {

const int n = stoneValue.size();

vector<int> sums(n + 1);

for (int i = 0; i < n; ++i)

sums[i + 1] = sums[i] + stoneValue[i];

vector<vector<int>> cache(n, vector<int>(n, -1));

// max value alice can get from range [l, r]

function<int(int, int)> dp = [&](int l, int r) {

if (l == r) return 0;

int& ans = cache[l][r];

if (ans != -1) return ans;

for (int k = l; k < r; ++k) {

// left: [l, k], right: [k + 1, r]

int sum_l = sums[k + 1] - sums[l];

int sum_r = sums[r + 1] - sums[k + 1];

if (sum_l > sum_r)

ans = max(ans, sum_r + dp(k + 1, r));

else if (sum_l < sum_r)

ans = max(ans, sum_l + dp(l, k));

else

ans = max(ans, sum_l + max(dp(l, k), dp(k + 1, r)));

}

return ans;

};

return dp(0, n - 1);

}

};

花花酱 LeetCode 1562. Find Latest Group of Size M

By zxi on August 23, 2020

Given an array arr that represents a permutation of numbers from 1 to n. You have a binary string of size n that initially has all its bits set to zero.

At each step i (assuming both the binary string and arr are 1-indexed) from 1 to n, the bit at position arr[i] is set to 1. You are given an integer m and you need to find the latest step at which there exists a group of ones of length m. A group of ones is a contiguous substring of 1s such that it cannot be extended in either direction.

Return the latest step at which there exists a group of ones of length exactly m. If no such group exists, return -1.

Example 1:

Input: arr = [3,5,1,2,4], m = 1
Output: 4
Explanation:
Step 1: "00100", groups: ["1"]
Step 2: "00101", groups: ["1", "1"]
Step 3: "10101", groups: ["1", "1", "1"]
Step 4: "11101", groups: ["111", "1"]
Step 5: "11111", groups: ["11111"]
The latest step at which there exists a group of size 1 is step 4.

Example 2:

Input: arr = [3,1,5,4,2], m = 2
Output: -1
Explanation:
Step 1: "00100", groups: ["1"]
Step 2: "10100", groups: ["1", "1"]
Step 3: "10101", groups: ["1", "1", "1"]
Step 4: "10111", groups: ["1", "111"]
Step 5: "11111", groups: ["11111"]
No group of size 2 exists during any step.

Example 3:

Input: arr = [1], m = 1
Output: 1

Example 4:

Input: arr = [2,1], m = 2
Output: 2

Constraints:

n == arr.length
1 <= n <= 10^5
1 <= arr[i] <= n
All integers in arr are distinct.
1 <= m <= arr.length

Solution: Hashtable

Similar to LC 128

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int findLatestStep(vector<int>& arr, int m) {

const int n = arr.size();

vector<int> len(n + 2);

vector<int> counts(n + 2);

int ans = -1;

for (int i = 0; i < n; ++i) {

const int x = arr[i];

const int l = len[x - 1];

const int r = len[x + 1];

const int t = 1 + l + r;

len[x - l] = len[x + r] = t;

--counts[l];

--counts[r];

++counts[t];

if (counts[m]) ans = i + 1;

}

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1568. Minimum Number of Days to Disconnect Island

Solution: Brute Force

C++

花花酱 LeetCode 1567. Maximum Length of Subarray With Positive Product

Solution: DP

C++

花花酱 LeetCode 1566. Detect Pattern of Length M Repeated K or More Times

Solution 1: Brute Force

C++

Solution 2: Shift and count

C++

花花酱 LeetCode 1563. Stone Game V

Solution: Range DP + Prefix Sum

C++

花花酱 LeetCode 1562. Find Latest Group of Size M

Solution: Hashtable

C++