Huahua’s Tech Road

花花酱 LeetCode 1561. Maximum Number of Coins You Can Get

By zxi on August 23, 2020

There are 3n piles of coins of varying size, you and your friends will take piles of coins as follows:

In each step, you will choose any 3 piles of coins (not necessarily consecutive).
Of your choice, Alice will pick the pile with the maximum number of coins.
You will pick the next pile with maximum number of coins.
Your friend Bob will pick the last pile.
Repeat until there are no more piles of coins.

Given an array of integers piles where piles[i] is the number of coins in the i^th pile.

Return the maximum number of coins which you can have.

Example 1:

Input: piles = [2,4,1,2,7,8]
Output: 9
Explanation: Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with 7 coins and Bob the last one.
Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with 2 coins and Bob the last one.
The maximum number of coins which you can have are: 7 + 2 = 9.
On the other hand if we choose this arrangement (1, 2, 8), (2, 4, 7) you only get 2 + 4 = 6 coins which is not optimal.

Example 2:

Input: piles = [2,4,5]
Output: 4

Example 3:

Input: piles = [9,8,7,6,5,1,2,3,4]
Output: 18

Constraints:

3 <= piles.length <= 10^5
piles.length % 3 == 0
1 <= piles[i] <= 10^4

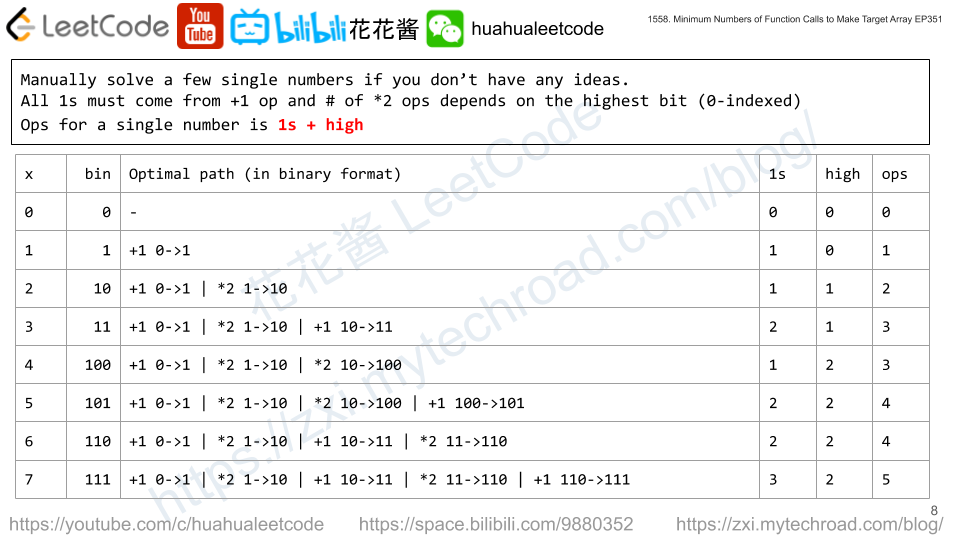
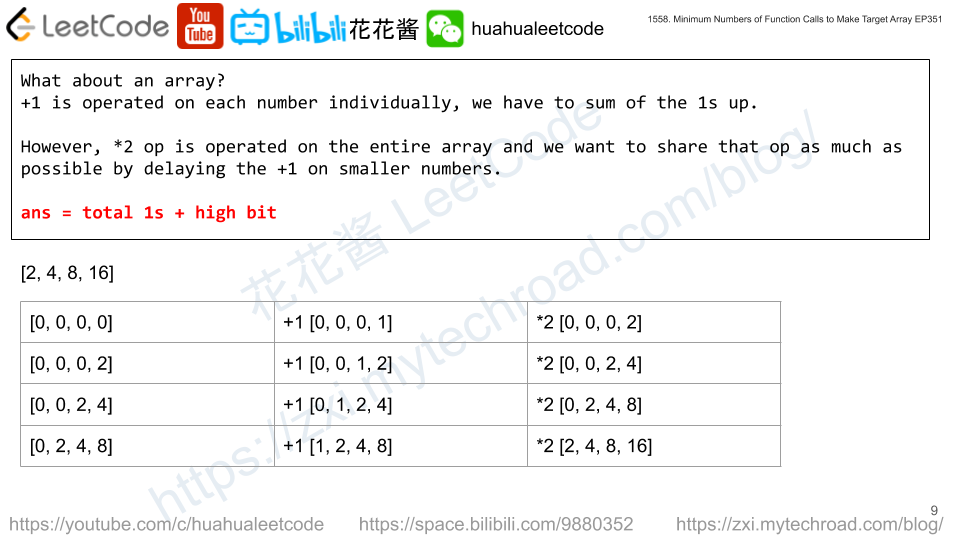
Solution: Greedy

Always take the second largest element of a in the sorted array.
[1, 2, 3, 4, 5, 6, 7, 8, 9]
tuples: (1, 8, 9), (2, 6, 7), (3, 4, 5)
Alice: 9, 7, 5
You: 8, 6, 4
Bob: 1, 2, 3

Time complexity: O(nlogn) -> O(n + k)
Space complexity: O(1)

C++

class Solution {

public:

int maxCoins(vector<int>& piles) {

const int n = piles.size() / 3;

sort(begin(piles), end(piles));

int ans = 0;

for (int i = 0; i < n; ++i)

ans += piles[n * 3 - 2 - i * 2];

return ans;

}

};

C++ counting sort

class Solution {

public:

int maxCoins(vector<int>& piles) {

constexpr int kMax = 10000;

const int n = piles.size() / 3;

vector<int> counts(kMax + 1);

for (int v : piles) ++counts[v];

int idx = 0;

for (int i = 1; i <= kMax; ++i)

while (counts[i]--) piles[idx++] = i;

int ans = 0;

for (int i = 0; i < n; ++i)

ans += piles[n * 3 - 2 - i * 2];

return ans;

}

};

花花酱 LeetCode 1560. Most Visited Sector in a Circular Track

By zxi on August 23, 2020

Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The i^th round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]

Return an array of the most visited sectors sorted in ascending order.

Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).

Example 1:

Input: n = 4, rounds = [1,3,1,2]
Output: [1,2]
Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.

Example 2:

Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2]
Output: [2]

Example 3:

Input: n = 7, rounds = [1,3,5,7]
Output: [1,2,3,4,5,6,7]

Constraints:

2 <= n <= 100
1 <= m <= 100
rounds.length == m + 1
1 <= rounds[i] <= n
rounds[i] != rounds[i + 1] for 0 <= i < m

Solution: Simulation

Time complexity: O(m*n)
Space complexity: O(n)

C++

class Solution {

public:

vector<int> mostVisited(int n, vector<int>& rounds) {

vector<int> counts(n);

counts[rounds[0] - 1] = 1;

for (int i = 1; i < rounds.size(); ++i)

for (int s = rounds[i - 1]; ; ++s) {

++counts[s %= n];

if (s == rounds[i] - 1) break;

}

const int max_count = *max_element(begin(counts), end(counts));

vector<int> ans;

for (int i = 0; i < n; ++i)

if (counts[i] == max_count) ans.push_back(i + 1);

return ans;

}

};

花花酱 LeetCode 1559. Detect Cycles in 2D Grid

By zxi on August 23, 2020

Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.

A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it – in one of the four directions (up, down, left, or right), if it has the same value of the current cell.

Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.

Return true if any cycle of the same value exists in grid, otherwise, return false.

Example 1:

Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below:

Example 2:

Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below:

Example 3:

Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false

Constraints:

m == grid.length
n == grid[i].length
1 <= m <= 500
1 <= n <= 500
grid consists only of lowercase English letters.

Solution: DFS

Finding a cycle in an undirected graph => visiting a node that has already been visited and it’s not the parent node of the current node.
b b
b b
null -> (0, 0) -> (0, 1) -> (1, 1) -> (1, 0) -> (0, 0)
The second time we visit (0, 0) which has already been visited before and it’s not the parent of the current node (1, 0) ( (1, 0)’s parent is (1, 1) ) which means we found a cycle.

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

class Solution {

public:

bool containsCycle(vector<vector<char>>& grid) {

const int m = grid.size();

const int n = grid[0].size();

vector<vector<int>> seen(m, vector<int>(n));

vector<int> dirs{0, 1, 0, -1, 0};

function<bool(int, int, int, int)> dfs = [&](int i, int j, int pi, int pj) {

++seen[i][j];

for (int d = 0; d < 4; ++d) {

int ni = i + dirs[d];

int nj = j + dirs[d + 1];

if (ni < 0 || nj < 0 || ni >= m || nj >= n) continue;

if (grid[ni][nj] != grid[i][j]) continue;

if (!seen[ni][nj]) {

if (dfs(ni, nj, i, j)) return true;

} else if (ni != pi || nj != pj) {

return true;

}

return false;

};

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

if (!seen[i][j]++ && dfs(i, j, -1, -1))

return true;

return false;

}

};

花花酱 LeetCode 1558. Minimum Numbers of Function Calls to Make Target Array

By zxi on August 22, 2020

Your task is to form an integer array nums from an initial array of zeros arr that is the same size as nums.

Return the minimum number of function calls to make nums from arr.

The answer is guaranteed to fit in a 32-bit signed integer.

Example 1:

Input: nums = [1,5]
Output: 5
Explanation: Increment by 1 (second element): [0, 0] to get [0, 1] (1 operation).
Double all the elements: [0, 1] -> [0, 2] -> [0, 4] (2 operations).
Increment by 1 (both elements)  [0, 4] -> [1, 4] -> [1, 5] (2 operations).
Total of operations: 1 + 2 + 2 = 5.

Example 2:

Input: nums = [2,2]
Output: 3
Explanation: Increment by 1 (both elements) [0, 0] -> [0, 1] -> [1, 1] (2 operations).
Double all the elements: [1, 1] -> [2, 2] (1 operation).
Total of operations: 2 + 1 = 3.

Example 3:

Input: nums = [4,2,5]
Output: 6
Explanation: (initial)[0,0,0] -> [1,0,0] -> [1,0,1] -> [2,0,2] -> [2,1,2] -> [4,2,4] -> [4,2,5](nums).

Example 4:

Input: nums = [3,2,2,4]
Output: 7

Example 5:

Input: nums = [2,4,8,16]
Output: 8

Constraints:

1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9

Solution: count 1s

For 5 (101b), we can add 1s for 5 times which of cause isn’t the best way to generate 5, the optimal way is to [+1, *2, +1]. We have to add 1 for each 1 in the binary format. e.g. 11 (1011), we need 3x “+1” op, and 4 “*2” op. Fortunately, the “*2” can be shared/delayed, thus we just need to find the largest number.
e.g. [2,4,8,16]
[0, 0, 0, 0] -> [0, 0, 0, 1] -> [0, 0, 0, 2]
[0, 0, 0, 2] -> [0, 0, 1, 2] -> [0, 0, 2, 4]
[0, 0, 2, 4] -> [0, 1, 2, 4] -> [0, 2, 4, 8]
[0, 2, 4, 8] -> [1, 2, 4, 8] -> [2, 4, 8, 16]
ans = sum{count_1(arr_i)} + high_bit(max(arr_i))

Time complexity: O(n*log(max(arr_i))
Space complexity: O(1)

C++

class Solution {

public:

int minOperations(vector<int>& nums) {

int ans = 0;

int high = 0;

for (int x : nums) {

high = max(high, 31 - __builtin_clz(x | 1));

ans += std::bitset<32>(x).count();

}

return ans + high;

}

};

Java

class Solution {

public int minOperations(int[] nums) {

int ans = 0;

int high = 0;

for (int x : nums) {

int l = -1;

while (x != 0) {

ans += x & 1;

x >>= 1;

++l;

}

high = Math.max(high, l);

}

return ans + high;

}

Python3

class Solution:

def minOperations(self, nums: List[int]) -> int:

return sum(bin(x).count('1') for x in nums) + len(bin(max(nums))) - 3

花花酱 LeetCode 1557. Minimum Number of Vertices to Reach All Nodes

By zxi on August 22, 2020

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [from_i, to_i] represents a directed edge from node from_i to node to_i.

Find the smallest set of vertices from which all nodes in the graph are reachable. It’s guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:

Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= from_i, to_i < n
All pairs (from_i, to_i) are distinct.

Solution: In degree

Nodes with 0 in degree will be the answer.
Time complexity: O(E+V)
Space complexity: O(V)

C++

class Solution {

public:

vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {

vector<int> in(n);

for (const auto& e : edges) ++in[e[1]];

vector<int> ans;

for (int i = 0; i < n; ++i)

if (in[i] == 0) ans.push_back(i);

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1561. Maximum Number of Coins You Can Get

Solution: Greedy

C++

C++ counting sort

花花酱 LeetCode 1560. Most Visited Sector in a Circular Track

Solution: Simulation

C++

花花酱 LeetCode 1559. Detect Cycles in 2D Grid

Solution: DFS

C++

花花酱 LeetCode 1558. Minimum Numbers of Function Calls to Make Target Array

Solution: count 1s

C++

Java

Python3

花花酱 LeetCode 1557. Minimum Number of Vertices to Reach All Nodes

Solution: In degree

C++