Huahua’s Tech Road

花花酱 LeetCode 1556. Thousand Separator

By zxi on August 22, 2020

Given an integer n, add a dot (“.”) as the thousands separator and return it in string format.

Example 1:

Input: n = 987
Output: "987"

Example 2:

Input: n = 1234
Output: "1.234"

Example 3:

Input: n = 123456789
Output: "123.456.789"

Example 4:

Input: n = 0
Output: "0"

Constraints:

0 <= n < 2^31

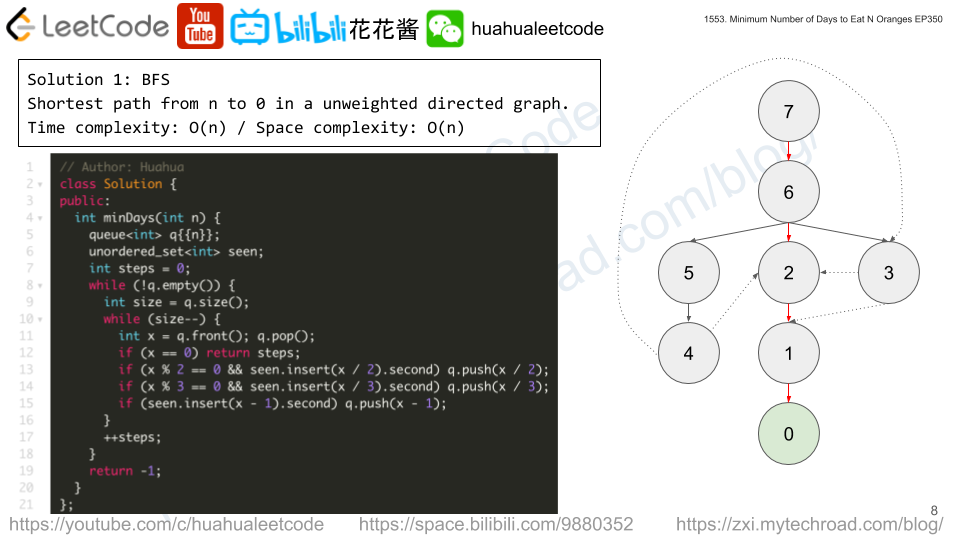
Solution: Digit by digit

Time complexity: O(log^2(n)) -> O(logn)
Space complexity: O(log(n))

C++

class Solution {

public:

string thousandSeparator(int n) {

string ans;

int count = 0;

do {

if (count++ % 3 == 0 && ans.size())

ans = "." + ans;

ans = to_string(n % 10) + ans;

n /= 10;

} while (n);

return ans;

}

};

花花酱 LeetCode 1553. Minimum Number of Days to Eat N Oranges

By zxi on August 16, 2020

There are n oranges in the kitchen and you decided to eat some of these oranges every day as follows:

Eat one orange.
If the number of remaining oranges (n) is divisible by 2 then you can eat n/2 oranges.
If the number of remaining oranges (n) is divisible by 3 then you can eat 2*(n/3) oranges.

You can only choose one of the actions per day.

Return the minimum number of days to eat n oranges.

Example 1:

Input: n = 10
Output: 4
Explanation: You have 10 oranges.
Day 1: Eat 1 orange,  10 - 1 = 9.  
Day 2: Eat 6 oranges, 9 - 2*(9/3) = 9 - 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 - 2*(3/3) = 3 - 2 = 1. 
Day 4: Eat the last orange  1 - 1  = 0.
You need at least 4 days to eat the 10 oranges.

Example 2:

Input: n = 6
Output: 3
Explanation: You have 6 oranges.
Day 1: Eat 3 oranges, 6 - 6/2 = 6 - 3 = 3. (Since 6 is divisible by 2).
Day 2: Eat 2 oranges, 3 - 2*(3/3) = 3 - 2 = 1. (Since 3 is divisible by 3)
Day 3: Eat the last orange  1 - 1  = 0.
You need at least 3 days to eat the 6 oranges.

Example 3:

Input: n = 1
Output: 1

Example 4:

Input: n = 56
Output: 6

Constraints:

1 <= n <= 2*10^9

Solution: Greedy + DP

Eat oranges one by one to make it a multiply of 2 or 3 such that we can eat 50% or 66.66…% of the oranges in one step.
dp(n) := min steps to finish n oranges.
base case n <= 1, dp(n) = n
transition: dp(n) = 1 + min(n%2 + dp(n/2), n % 3 + dp(n / 3))
e.g. n = 11,
we eat 11%2 = 1 in one step, left = 10 and then eat 10 / 2 = 5 in another step. 5 left for the subproblem.
we eat 11%3 = 2 in two steps, left = 9 and then eat 9 * 2 / 3 = 6 in another step, 3 left for the subproblem.
dp(11) = 1 + min(1 + dp(5), 2 + dp(3))

T(n) = 2*T(n/2) + O(1) = O(n)
Time complexity: O(n) // w/o memoization, close to O(logn) in practice.
Space complexity: O(logn)

C++

class Solution {

public:

int minDays(int n) {

unordered_map<int, int> cache;

function<int(int)> dp = [&](int n) {

if (n <= 1) return n;

auto it = cache.find(n);

if (it != cache.end()) return it->second;

return cache[n] = 1 + min(n % 2 + dp(n / 2), n % 3 + dp(n / 3));

};

return dp(n);

}

};

Java

class Solution {

private static Map<Integer, Integer> cache = new HashMap<>();

public int minDays(int n) {

return dp(n);

}

private int dp(int n) {

if (n <= 1) return n;

if (cache.containsKey(n)) return cache.get(n);

int ans = 1 + Math.min(n % 2 + dp(n / 2), n % 3 + dp(n / 3));

cache.put(n, ans);

return ans;

}

Python3

class Solution:

def minDays(self, n: int) -> int:

@lru_cache(None)

def dp(n):

if n <= 1: return n

return 1 + min(n % 2 + dp(n // 2), n % 3 + dp(n // 3))

return dp(n)

Solution 2: BFS

if x % 2 == 0, push x/2 onto the queue
if x % 3 == 0, push x/3 onto the queue
always push x – 1 onto the queue

C++

class Solution {

public:

int minDays(int n) {

queue<int> q{{n}};

unordered_set<int> seen;

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

int x = q.front(); q.pop();

if (x == 0) return steps;

if (x % 2 == 0 && seen.insert(x / 2).second)

q.push(x / 2);

if (x % 3 == 0 && seen.insert(x / 3).second)

q.push(x / 3);

if (seen.insert(x - 1).second)

q.push(x - 1);

}

++steps;

}

return -1;

}

};

花花酱 LeetCode 1552. Magnetic Force Between Two Balls

By zxi on August 15, 2020

In universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the i^th basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.

Rick stated that magnetic force between two different balls at positions x and y is |x - y|.

Given the integer array position and the integer m. Return the required force.

Example 1:

Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.

Example 2:

Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.

Constraints:

n == position.length
2 <= n <= 10^5
1 <= position[i] <= 10^9
All integers in position are distinct.
2 <= m <= position.length

Solution: Binary Search

Find the max distance that we can put m balls.

Time complexity: O(n*log(distance))
Space complexity: O(1)

C++

class Solution {

public:

int maxDistance(vector<int>& position, int m) {

const int n = position.size();

sort(begin(position), end(position));

auto count = [&](int d) -> int {

int last = position[0];

int ans = 1;

for (int x : position) {

if (x - last >= d) {

last = x;

++ans;

}

return ans;

};

int l = 0;

int t = (position.back() - position.front()) + 1;

int r = t;

while (l < r) {

int mid = l + (r - l) / 2;

if (count(t - mid) >= m) // find min of l => max of t - l

r = mid;

else

l = mid + 1;

}

return t - l;

}

};

Java

class Solution {

public int maxDistance(int[] position, int m) {

Arrays.sort(position);

final int n = position.length;

int l = 0;

int r = position[n - 1] - position[0] + 1;

int t = r;

while (l < r) {

int mid = l + (r - l) / 2;

if (getCount(position, t - mid) >= m)

r = mid;

else

l = mid + 1;

}

return t - l;

}

private int getCount(int[] position, int d) {

int count = 1;

int last = position[0];

for (int x : position) {

if (x - last >= d) {

++count;

last = x;

}

return count;

}

Python3

class Solution:

def maxDistance(self, position: List[int], m: int) -> int:

position.sort()

def getCount(d: int) -> int:

last, count = position[0], 1

for x in position:

if x - last >= d:

last = x

count += 1

return count

l, r = 0, position[-1] - position[0] + 1

t = r

while l < r:

mid = l + (r - l) // 2

if getCount(t - mid) >= m:

r = mid

else:

l = mid + 1

return t - l

花花酱 LeetCode 1551. Minimum Operations to Make Array Equal

By zxi on August 15, 2020

You have an array arr of length n where arr[i] = (2 * i) + 1 for all valid values of i (i.e. 0 <= i < n).

In one operation, you can select two indices x and y where 0 <= x, y < n and subtract 1 from arr[x] and add 1 to arr[y] (i.e. perform arr[x] -=1 and arr[y] += 1). The goal is to make all the elements of the array equal. It is guaranteed that all the elements of the array can be made equal using some operations.

Given an integer n, the length of the array. Return the minimum number of operations needed to make all the elements of arr equal.

Example 1:

Input: n = 3
Output: 2
Explanation: arr = [1, 3, 5]
First operation choose x = 2 and y = 0, this leads arr to be [2, 3, 4]
In the second operation choose x = 2 and y = 0 again, thus arr = [3, 3, 3].

Example 2:

Input: n = 6
Output: 9

Constraints:

1 <= n <= 10^4

Solution: Math

1: Find the mean (final value) of the array, assuming x, easy to show x == n
2: Compute the sum of an arithmetic progression of (x – 1) + (x – 3) + … for n // 2 pairs

e.g. n = 6
arr = [1, 3, 5, 7, 9, 11]
x = (1 + 2 * n – 1) / 2 = 6 = n
steps = (6 – 1) + (6 – 3) + (6 – 5) = (n // 2) * (n – (1 + n – 1) / 2) = (n // 2) * (n – n // 2) = 3 * 3 = 9

e.g. n = 5
arr = [1,3,5,7,9]
x = (1 + 2 * n – 1) / 2 = 5 = n
steps = (5 – 1) + (5 – 3)= (n//2) * (n – n // 2) = (n // 2) * ((n + 1) // 2) = 2 * 3 = 6

Time complexity: O(1)
Space complexity: O(1)

C++

class Solution {

public:

int minOperations(int n) {

return (n / 2) * ((n + 1) / 2);

}

};

花花酱 LeetCode 1550. Three Consecutive Odds

By zxi on August 15, 2020

Given an integer array arr, return true if there are three consecutive odd numbers in the array. Otherwise, return false.

Example 1:

Input: arr = [2,6,4,1]
Output: false
Explanation: There are no three consecutive odds.

Example 2:

Input: arr = [1,2,34,3,4,5,7,23,12]
Output: true
Explanation: [5,7,23] are three consecutive odds.

Constraints:

1 <= arr.length <= 1000
1 <= arr[i] <= 1000

Solution: Counting

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

bool threeConsecutiveOdds(vector<int>& arr) {

int count = 0;

for (int x : arr) {

if (x & 1) {

if (++count == 3) return true;

} else {

count = 0;

}

return false;

}

};

Huahua's Tech Road

花花酱 LeetCode 1556. Thousand Separator

C++

花花酱 LeetCode 1553. Minimum Number of Days to Eat N Oranges

Solution: Greedy + DP

C++

Java

Python3

Solution 2: BFS

C++

花花酱 LeetCode 1552. Magnetic Force Between Two Balls

Solution: Binary Search

C++

Java

Python3

花花酱 LeetCode 1551. Minimum Operations to Make Array Equal

Solution: Math

C++

花花酱 LeetCode 1550. Three Consecutive Odds

Solution: Counting

C++