Huahua’s Tech Road

花花酱 LeetCode 1482. Minimum Number of Days to Make m Bouquets

By zxi on June 14, 2020

Given an integer array bloomDay, an integer m and an integer k.

We need to make m bouquets. To make a bouquet, you need to use k adjacent flowers from the garden.

The garden consists of n flowers, the ith flower will bloom in the bloomDay[i] and then can be used in exactly one bouquet.

Return the minimum number of days you need to wait to be able to make m bouquets from the garden. If it is impossible to make m bouquets return -1.

Example 1:

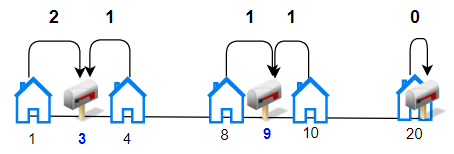
Input: bloomDay = [1,10,3,10,2], m = 3, k = 1
Output: 3
Explanation: Let's see what happened in the first three days. x means flower bloomed and _ means flower didn't bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: [x, _, _, _, _]   // we can only make one bouquet.
After day 2: [x, _, _, _, x]   // we can only make two bouquets.
After day 3: [x, _, x, _, x]   // we can make 3 bouquets. The answer is 3.

Example 2:

Input: bloomDay = [1,10,3,10,2], m = 3, k = 2
Output: -1
Explanation: We need 3 bouquets each has 2 flowers, that means we need 6 flowers. We only have 5 flowers so it is impossible to get the needed bouquets and we return -1.

Example 3:

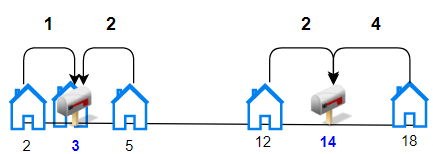
Input: bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
Output: 12
Explanation: We need 2 bouquets each should have 3 flowers.
Here's the garden after the 7 and 12 days:
After day 7: [x, x, x, x, _, x, x]
We can make one bouquet of the first three flowers that bloomed. We cannot make another bouquet from the last three flowers that bloomed because they are not adjacent.
After day 12: [x, x, x, x, x, x, x]
It is obvious that we can make two bouquets in different ways.

Example 4:

Input: bloomDay = [1000000000,1000000000], m = 1, k = 1
Output: 1000000000
Explanation: You need to wait 1000000000 days to have a flower ready for a bouquet.

Example 5:

Input: bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2
Output: 9

Constraints:

bloomDay.length == n
1 <= n <= 10^5
1 <= bloomDay[i] <= 10^9
1 <= m <= 10^6
1 <= k <= n

Solution: Binary Search

Find the smallest day D that we can make at least m bouquets using binary search.

at a given day, we can check how many bouquets we can make in O(n)

Time complexity: O(nlog(max(days))
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minDays(vector<int>& bloomDay, int m, int k) {

const auto [lo, hi] = minmax_element(begin(bloomDay), end(bloomDay));

const int kInf = *hi + 1;

int l = *lo;

int r = kInf;

// Return the number of bouquets we can get at day D.

auto getBouquets = [&](int D) {

int ans = 0;

int cur = 0;

for (int d : bloomDay) {

if (d > D) {

cur = 0;

} else if (++cur == k) {

++ans;

cur = 0;

}

return ans;

};

while (l < r) {

int mid = l + (r - l) / 2;

// Find smallest day that bouquets >= m.

if (getBouquets(mid) >= m)

r = mid;

else

l = mid + 1;

}

return l >= kInf ? -1 : l;

}

};

花花酱 LeetCode 1481. Least Number of Unique Integers after K Removals

By zxi on June 14, 2020

Given an array of integers arr and an integer k. Find the least number of unique integers after removing exactly k elements.

Example 1:

Input: arr = [5,5,4], k = 1
Output: 1
Explanation: Remove the single 4, only 5 is left.

Example 2:

Input: arr = [4,3,1,1,3,3,2], k = 3
Output: 2
Explanation: Remove 4, 2 and either one of the two 1s or three 3s. 1 and 3 will be left.

Constraints:

1 <= arr.length <= 10^5
1 <= arr[i] <= 10^9
0 <= k <= arr.length

Solution: Greedy

Count the frequency of each unique number. Sort by frequency, remove items with lowest frequency first.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int findLeastNumOfUniqueInts(vector<int>& arr, int k) {

unordered_map<int, int> c;

for (int x : arr) ++c[x];

vector<int> m; // freq

for (const auto [x, f] : c)

m.push_back(f);

sort(begin(m), end(m));

int ans = m.size();

int i = 0;

while (k--) {

if (--m[i] == 0) {

++i;

--ans;

}

return ans;

}

};

花花酱 LeetCode 1480. Running Sum of 1d Array

By zxi on June 14, 2020

Given an array nums. We define a running sum of an array as runningSum[i] = sum(nums[0]…nums[i]).

Return the running sum of nums.

Example 1:

Input: nums = [1,2,3,4]
Output: [1,3,6,10]
Explanation: Running sum is obtained as follows: [1, 1+2, 1+2+3, 1+2+3+4].

Example 2:

Input: nums = [1,1,1,1,1]
Output: [1,2,3,4,5]
Explanation: Running sum is obtained as follows: [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1].

Example 3:

Input: nums = [3,1,2,10,1]
Output: [3,4,6,16,17]

Constraints:

1 <= nums.length <= 1000
-10^6 <= nums[i] <= 10^6

Solution

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<int> runningSum(vector<int>& nums) {

vector<int> ans(nums);

for (int i = 1; i < ans.size(); ++i)

ans[i] += ans[i - 1];

return ans;

}

};

花花酱 LeetCode 1478. Allocate Mailboxes

By zxi on June 14, 2020

Given the array houses and an integer k. where houses[i] is the location of the ith house along a street, your task is to allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The answer is guaranteed to fit in a 32-bit signed integer.

Example 1:

Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5

Example 2:

Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

Example 3:

Input: houses = [7,4,6,1], k = 1
Output: 8

Example 4:

Input: houses = [3,6,14,10], k = 4
Output: 0

Constraints:

n == houses.length
1 <= n <= 100
1 <= houses[i] <= 10^4
1 <= k <= n
Array houses contain unique integers.

Solution: DP

First, we need to sort the houses by their location.

This is a partitioning problem, e.g. optimal solution to partition first N houses into K groups. (allocating K mailboxes for the first N houses).

The key of this problem is to solve a base case, optimally allocating one mailbox for houses[i~j], The intuition is to put the mailbox in the middle location, this only works if there are only tow houses, or all the houses are evenly distributed. The correct location is the “median position” of a set of houses. For example, if the sorted locations are [1,2,3,100], the average will be 26 which costs 146 while the median is 2, and the cost becomes 100.

dp[i][k] := min cost to allocate k mailboxes houses[0~i].

base cases:

dp[i][1] = cost(0, i), min cost to allocate one mailbox.
dp[i][k] = 0 if k > i, more mailboxes than houses. // this is actually a pruning.

transition:

dp[i][k] = min(dp[p][k-1] + cost(p + 1, i)) 0 <= p < i,

allocate k-1 mailboxes for houses[0~p], and allocate one for houses[p+1~i]

ans:

dp[n-1][k]

Time complexity: O(n^3)
Space complexity: O(n^2) -> O(n)

C++

// Author: Huahua

class Solution {

public:

int minDistance(vector<int>& houses, int k) {

constexpr int kInf = 1e9;

const int n = houses.size();

sort(begin(houses), end(houses));

vector<vector<int>> dp(n + 1, vector<int>(n + 1, kInf));

vector<vector<int>> costs(n + 1, vector<int>(n + 1, kInf));

// min cost to allocate one mailbox for houses[i~j].

auto cost = [&](int i, int j) {

int& ans = costs[i][j];

if (ans != kInf) return ans;

const int m = i + (j - i) / 2;

int box = 0;

if ((j - i + 1) & 1) // odd number of houses.

box = houses[m];

else // even number of houses.

box = (houses[m] + houses[m + 1]) / 2;

ans = 0;

for (int h = i; h <= j; ++h)

ans += abs(houses[h] - box);

return ans;

};

// min cost to allocate k mailboxes for houses[0~i].

function<int(int, int)> solve = [&](int i, int k) {

if (k > i) return 0; // more mailboxs than houses.

if (k == 1) return cost(0, i);

int& ans = dp[i][k];

if (ans != kInf) return ans;

for (int p = 0; p < i; ++p)

ans = min(ans, solve(p, k - 1) + cost(p + 1, i));

return ans;

};

return solve(n - 1, k);

}

};

O(1) time to compute cost. O(n) Time and space for pre-processing.

C++

// Author: Huahua

vector<int> sums(n + 1);

for (int i = 1; i <= n; ++i)

sums[i] = sums[i - 1] + houses[i - 1];

// min cost to allocate one mailbox for houses[i~j].

auto cost = [&](int i, int j) {

const int m1 = (i + j) / 2;

const int m2 = (i + j + 1) / 2;

const int center = (houses[m1] + houses[m2]) / 2;

return (m1 - i + 1) * center - (sums[m1 + 1] - sums[i])

+ (sums[j + 1] - sums[m2]) - (j - m2 + 1) * center;

};

花花酱 LeetCode 1477. Find Two Non-overlapping Sub-arrays Each With Target Sum

By zxi on June 13, 2020

Given an array of integers arr and an integer target.

You have to find two non-overlapping sub-arrays of arr each with sum equal target. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is minimum.

Return the minimum sum of the lengths of the two required sub-arrays, or return -1 if you cannot find such two sub-arrays.

Example 1:

Input: arr = [3,2,2,4,3], target = 3
Output: 2
Explanation: Only two sub-arrays have sum = 3 ([3] and [3]). The sum of their lengths is 2.

Example 2:

Input: arr = [7,3,4,7], target = 7
Output: 2
Explanation: Although we have three non-overlapping sub-arrays of sum = 7 ([7], [3,4] and [7]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.

Example 3:

Input: arr = [4,3,2,6,2,3,4], target = 6
Output: -1
Explanation: We have only one sub-array of sum = 6.

Example 4:

Input: arr = [5,5,4,4,5], target = 3
Output: -1
Explanation: We cannot find a sub-array of sum = 3.

Example 5:

Input: arr = [3,1,1,1,5,1,2,1], target = 3
Output: 3
Explanation: Note that sub-arrays [1,2] and [2,1] cannot be an answer because they overlap.

Constraints:

1 <= arr.length <= 10^5
1 <= arr[i] <= 1000
1 <= target <= 10^8

Solution: Sliding Window + Best so far

Use a sliding window to maintain a subarray whose sum is <= target
When the sum of the sliding window equals to target, we found a subarray [s, e]
Update ans with it’s length + shortest subarray which ends before s.
We can use an array to store the shortest subarray which ends before s.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int minSumOfLengths(vector<int>& arr, int target) {

constexpr int kInf = 1e9;

const int n = arr.size();

// min_lens[i] := min length of a valid subarray ends or before i.

vector<int> min_lens(n, kInf);

int ans = kInf;

int sum = 0;

int s = 0;

int min_len = kInf;

for (int e = 0; e < n; ++e) {

sum += arr[e];

while (sum > target) sum -= arr[s++];

if (sum == target) {

const int cur_len = e - s + 1;

if (s > 0 && min_lens[s - 1] != kInf)

ans = min(ans, cur_len + min_lens[s - 1]);

min_len = min(min_len, cur_len);

}

min_lens[e] = min_len;

}

return ans >= kInf ? -1 : ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1482. Minimum Number of Days to Make m Bouquets

Solution: Binary Search

C++

花花酱 LeetCode 1481. Least Number of Unique Integers after K Removals

Solution: Greedy

C++

花花酱 LeetCode 1480. Running Sum of 1d Array

Solution

C++

花花酱 LeetCode 1478. Allocate Mailboxes

Solution: DP

C++

C++

花花酱 LeetCode 1477. Find Two Non-overlapping Sub-arrays Each With Target Sum

Solution: Sliding Window + Best so far

C++