Huahua’s Tech Road

花花酱 LeetCode 1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit

By zxi on May 3, 2020

Given an array of integers nums and an integer limit, return the size of the longest continuous subarray such that the absolute difference between any two elements is less than or equal to limit.

In case there is no subarray satisfying the given condition return 0.

Example 1:

Input: nums = [8,2,4,7], limit = 4
Output: 2 
Explanation: All subarrays are: 
[8] with maximum absolute diff |8-8| = 0 <= 4.
[8,2] with maximum absolute diff |8-2| = 6 > 4. 
[8,2,4] with maximum absolute diff |8-2| = 6 > 4.
[8,2,4,7] with maximum absolute diff |8-2| = 6 > 4.
[2] with maximum absolute diff |2-2| = 0 <= 4.
[2,4] with maximum absolute diff |2-4| = 2 <= 4.
[2,4,7] with maximum absolute diff |2-7| = 5 > 4.
[4] with maximum absolute diff |4-4| = 0 <= 4.
[4,7] with maximum absolute diff |4-7| = 3 <= 4.
[7] with maximum absolute diff |7-7| = 0 <= 4. 
Therefore, the size of the longest subarray is 2.

Example 2:

Input: nums = [10,1,2,4,7,2], limit = 5
Output: 4 
Explanation: The subarray [2,4,7,2] is the longest since the maximum absolute diff is |2-7| = 5 <= 5.

Example 3:

Input: nums = [4,2,2,2,4,4,2,2], limit = 0
Output: 3

Constraints:

1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= limit <= 10^9

Solution 1: Sliding Window + TreeSet

Use a treeset to maintain a range of [l, r] such that max(nums[l~r]) – min(nums[l~r]) <= limit.
Every time, we add nums[r] into the tree, and move l towards r to keep the max diff under limit.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int longestSubarray(vector<int>& nums, int limit) {

multiset<int> s;

int l = 0;

int ans = 0;

for (int r = 0; r < nums.size(); ++r) {

s.insert(nums[r]);

while (*rbegin(s) - *begin(s) > limit)

s.erase(s.equal_range(nums[l++]).first);

ans = max(ans, r - l + 1);

}

return ans;

}

};

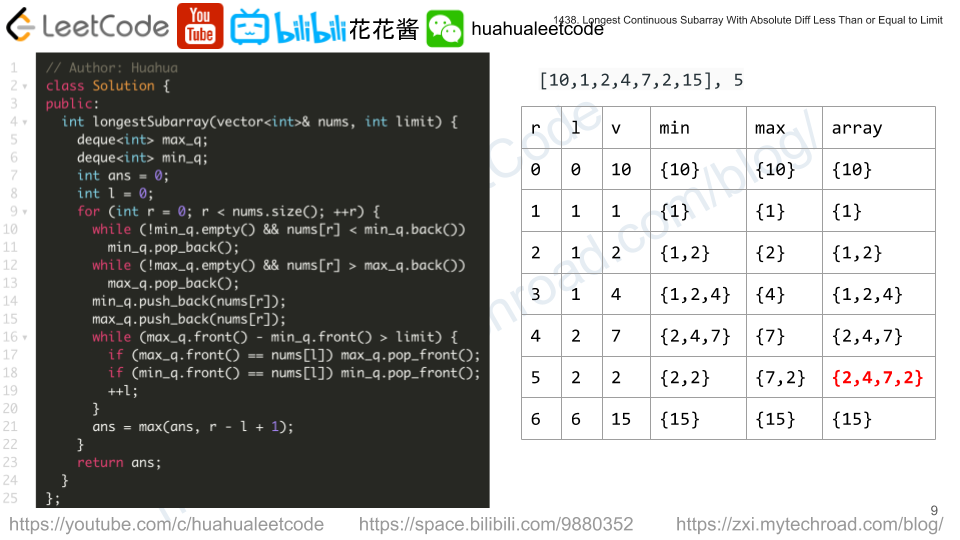
Solution 2: Dual Monotonic Queue

We want to maintain a range [l, r] that max(nums[l~r]) – min(nums[l~r]) <= limit, to track the max/min of a range efficiently we could use monotonic queue. One for max and one for min.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int longestSubarray(vector<int>& nums, int limit) {

deque<int> max_q;

deque<int> min_q;

int ans = 0;

int l = 0;

for (int r = 0; r < nums.size(); ++r) {

while (!min_q.empty() && nums[r] < min_q.back())

min_q.pop_back();

while (!max_q.empty() && nums[r] > max_q.back())

max_q.pop_back();

min_q.push_back(nums[r]);

max_q.push_back(nums[r]);

while (max_q.front() - min_q.front() > limit) {

if (max_q.front() == nums[l]) max_q.pop_front();

if (min_q.front() == nums[l]) min_q.pop_front();

++l;

}

ans = max(ans, r - l + 1);

}

return ans;

}

};

花花酱 LeetCode 1437. Check If All 1’s Are at Least Length K Places Away

By zxi on May 3, 2020

Given an array nums of 0s and 1s and an integer k, return True if all 1’s are at least k places away from each other, otherwise return False.

Example 1:

Input: nums = [1,0,0,0,1,0,0,1], k = 2
Output: true
Explanation: Each of the 1s are at least 2 places away from each other.

Example 2:

Input: nums = [1,0,0,1,0,1], k = 2
Output: false
Explanation: The second 1 and third 1 are only one apart from each other.

Example 3:

Input: nums = [1,1,1,1,1], k = 0
Output: true

Example 4:

Input: nums = [0,1,0,1], k = 1
Output: true

Constraints:

1 <= nums.length <= 10^5
0 <= k <= nums.length
nums[i] is 0 or 1

Solution: Scan the array

Only need to check adjacent ones. This problem should be easy instead of medium.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool kLengthApart(vector<int>& nums, int k) {

int d = k + 1; // distant enough

for (int n : nums) {

if (n == 0) {

++d;

} else {

if (d < k) return false;

d = 0;

}

return true;

}

};

花花酱 LeetCode 1436. Destination City

By zxi on May 3, 2020

You are given the array paths, where paths[i] = [cityA_i, cityB_i] means there exists a direct path going from cityA_i to cityB_i. Return the destination city, that is, the city without any path outgoing to another city.

It is guaranteed that the graph of paths forms a line without any loop, therefore, there will be exactly one destination city.

Example 1:

Input: paths = [["London","New York"],["New York","Lima"],["Lima","Sao Paulo"]]
Output: "Sao Paulo" 
Explanation: Starting at "London" city you will reach "Sao Paulo" city which is the destination city. Your trip consist of: "London" -> "New York" -> "Lima" -> "Sao Paulo".

Example 2:

Input: paths = [["B","C"],["D","B"],["C","A"]]
Output: "A"
Explanation: All possible trips are: 
"D" -> "B" -> "C" -> "A". 
"B" -> "C" -> "A". 
"C" -> "A". 
"A". 
Clearly the destination city is "A".

Example 3:

Input: paths = [["A","Z"]]
Output: "Z"

Constraints:

1 <= paths.length <= 100
paths[i].length == 2
1 <= cityA_i.length, cityB_i.length <= 10
cityA_i!= cityB_i
All strings consist of lowercase and uppercase English letters and the space character.

Solution: Count in / out degree for each node

Note: this is a more general solution to this type of problems.

Time complexity: O(n)
Space complexity: O(n)

Destination City: in_degree == 1 and out_degree == 0

C++

// Author: Huahua

class Solution {

public:

string destCity(vector<vector<string>>& paths) {

unordered_map<string, int> in, out;

for (const auto& path : paths) {

++out[path[0]];

++in[path[1]];

}

for (const auto& [city, degree] : in)

if (degree == 1 && out[city] == 0) return city;

return "";

}

};

花花酱 LeetCode 1434. Number of Ways to Wear Different Hats to Each Other

By zxi on May 3, 2020

There are n people and 40 types of hats labeled from 1 to 40.

Given a list of list of integers hats, where hats[i] is a list of all hats preferred by the i-th person.

Return the number of ways that the n people wear different hats to each other.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: hats = [[3,4],[4,5],[5]]
Output: 1
Explanation: There is only one way to choose hats given the conditions. 
First person choose hat 3, Second person choose hat 4 and last one hat 5.

Example 2:

Input: hats = [[3,5,1],[3,5]]
Output: 4
Explanation: There are 4 ways to choose hats
(3,5), (5,3), (1,3) and (1,5)

Example 3:

Input: hats = [[1,2,3,4],[1,2,3,4],[1,2,3,4],[1,2,3,4]]
Output: 24
Explanation: Each person can choose hats labeled from 1 to 4.
Number of Permutations of (1,2,3,4) = 24.

Example 4:

Input: hats = [[1,2,3],[2,3,5,6],[1,3,7,9],[1,8,9],[2,5,7]]
Output: 111

Constraints:

n == hats.length
1 <= n <= 10
1 <= hats[i].length <= 40
1 <= hats[i][j] <= 40
hats[i] contains a list of unique integers.

Solution: DP

dp[i][j] := # of ways using first i hats, j is the bit mask of people wearing hats.

e.g. dp[3][101] == # of ways using first 3 hats that people 1 and 3 are wearing hats.

init dp[0][0] = 1

dp[i][mask | (1 << p)] = dp[i-1][mask | (1 << p)] + dp[i-1][mask], where people p prefers hats i.

ans: dp[nHat][1…1]

Time complexity: O(2^n * h * n)
Space complexity: O(2^n * h) -> O(2^n)

C++

// Author: Huahua

class Solution {

public:

int numberWays(vector<vector<int>>& hats) {

constexpr int kHat = 40;

constexpr int kMod = 1e9 + 7;

const int n = hats.size();

vector<vector<int>> people(kHat + 1); // hat -> {people}

for (int i = 0; i < n; ++i)

for (int hat : hats[i])

people[hat].push_back(i);

// dp[i][j] := # of ways using first i hats where j is bit mask of people wearing hats.

vector<vector<int>> dp(kHat + 1, vector<int>(1 << n));

dp[0][0] = 1;

for (int i = 1; i <= kHat; ++i) {

dp[i] = dp[i - 1];

for (int mask = (1 << n) - 1; mask >= 0; --mask)

for (int p : people[i]) {

if (mask & (1 << p)) continue;

dp[i][mask | (1 << p)] += dp[i - 1][mask];

dp[i][mask | (1 << p)] %= kMod;

}

return dp.back().back();

}

};

O(2^n) memory

C++

// Author: Huahua

class Solution {

public:

int numberWays(vector<vector<int>>& hats) {

constexpr int kHat = 40;

constexpr int kMod = 1e9 + 7;

const int n = hats.size();

vector<vector<int>> people(kHat + 1); // hat -> {people}

for (int i = 0; i < n; ++i)

for (int hat : hats[i])

people[hat].push_back(i);

// dp([i])[j] := # of ways using first i hats where j is bit mask of people wearing hat.

vector<int> dp(1 << n);

dp[0] = 1;

for (int i = 1; i <= kHat; ++i)

for (int mask = (1 << n) - 1; mask >= 0; --mask)

for (int p : people[i]) {

if (mask & (1 << p)) continue;

dp[mask | (1 << p)] += dp[mask];

dp[mask | (1 << p)] %= kMod;

}

return dp.back();

}

};

LeetCode 1433. Check If a String Can Break Another String

By zxi on May 3, 2020

Given two strings: s1 and s2 with the same size, check if some permutation of string s1 can break some permutation of string s2 or vice-versa (in other words s2 can break s1).

A string x can break string y (both of size n) if x[i] >= y[i] (in alphabetical order) for all i between 0 and n-1.

Example 1:

Input: s1 = "abc", s2 = "xya"
Output: true
Explanation: "ayx" is a permutation of s2="xya" which can break to string "abc" which is a permutation of s1="abc".

Example 2:

Input: s1 = "abe", s2 = "acd"
Output: false 
Explanation: All permutations for s1="abe" are: "abe", "aeb", "bae", "bea", "eab" and "eba" and all permutation for s2="acd" are: "acd", "adc", "cad", "cda", "dac" and "dca". However, there is not any permutation from s1 which can break some permutation from s2 and vice-versa.

Example 3:

Input: s1 = "leetcodee", s2 = "interview"
Output: true

Constraints:

s1.length == n
s2.length == n
1 <= n <= 10^5
All strings consist of lowercase English letters.

Solution 1: Sort and compare

Time complexity: O(nlogn)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool checkIfCanBreak(string s1, string s2) {

sort(begin(s1), end(s1));

sort(begin(s2), end(s2));

int f1 = 1;

int f2 = 1;

for (int i = 0; i < s1.size(); ++i) {

f1 &= s1[i] <= s2[i];

f2 &= s1[i] >= s2[i];

}

return f1 || f2;

}

};

Solution 2: Counting Sort

The cumulative number of elements must be monotonic e.g. t1 >= t2 or t2 >= t1 for all the letters.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool checkIfCanBreak(string s1, string s2) {

vector<int> c1(26);

vector<int> c2(26);

for (int i = 0; i < s1.length(); ++i) {

++c1[s1[i] - 'a'];

++c2[s2[i] - 'a'];

}

int t1 = 0;

int t2 = 0;

int f1 = 1;

int f2 = 1;

for (int i = 0; i < 26; ++i) {

t1 += c1[i];

t2 += c2[i];

f1 &= t1 <= t2;

f2 &= t2 <= t1;

}

return f1 || f2;

}

};

Huahua's Tech Road

花花酱 LeetCode 1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit

Solution 1: Sliding Window + TreeSet

C++

Solution 2: Dual Monotonic Queue

C++

花花酱 LeetCode 1437. Check If All 1’s Are at Least Length K Places Away

Solution: Scan the array

C++

花花酱 LeetCode 1436. Destination City

Solution: Count in / out degree for each node

C++

花花酱 LeetCode 1434. Number of Ways to Wear Different Hats to Each Other

Solution: DP

C++

C++

LeetCode 1433. Check If a String Can Break Another String

Solution 1: Sort and compare

C++

Solution 2: Counting Sort

C++