Huahua’s Tech Road

花花酱 LeetCode 2074. Reverse Nodes in Even Length Groups

By zxi on November 15, 2021

You are given the head of a linked list.

The nodes in the linked list are sequentially assigned to non-empty groups whose lengths form the sequence of the natural numbers (1, 2, 3, 4, ...). The length of a group is the number of nodes assigned to it. In other words,

The 1^st node is assigned to the first group.
The 2^nd and the 3^rd nodes are assigned to the second group.
The 4^th, 5^th, and 6^th nodes are assigned to the third group, and so on.

Note that the length of the last group may be less than or equal to 1 + the length of the second to last group.

Reverse the nodes in each group with an even length, and return the head of the modified linked list.

Example 1:

Input: head = [5,2,6,3,9,1,7,3,8,4]
Output: [5,6,2,3,9,1,4,8,3,7]
Explanation:
- The length of the first group is 1, which is odd, hence no reversal occurrs.
- The length of the second group is 2, which is even, hence the nodes are reversed.
- The length of the third group is 3, which is odd, hence no reversal occurrs.
- The length of the last group is 4, which is even, hence the nodes are reversed.

Example 2:

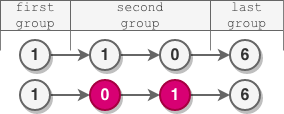
Input: head = [1,1,0,6]
Output: [1,0,1,6]
Explanation:
- The length of the first group is 1. No reversal occurrs.
- The length of the second group is 2. The nodes are reversed.
- The length of the last group is 1. No reversal occurrs.

Example 3:

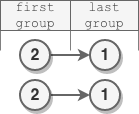
Input: head = [2,1]
Output: [2,1]
Explanation:
- The length of the first group is 1. No reversal occurrs.
- The length of the last group is 1. No reversal occurrs.

Example 4:

Input: head = [8]
Output: [8]
Explanation: There is only one group whose length is 1. No reversal occurrs.

Constraints:

The number of nodes in the list is in the range [1, 10⁵].
0 <= Node.val <= 10⁵

Solution: List

Reuse ReverseList from 花花酱 LeetCode 206. Reverse Linked List

Time complexity: O(n)
Space complexity: O(1)

C++

class Solution {

public:

ListNode* reverseEvenLengthGroups(ListNode* head) {

ListNode dummy(0, head);

ListNode* prev = &dummy;

auto reverse = [](ListNode* head) {

ListNode* prev = nullptr;

while (head) {

ListNode* next = head->next;

head->next = prev;

prev = head;

head = next;

}

return prev;

};

for (int k = 1; head; ++k) {

ListNode* tail = head;

int l = 1;

while (l < k && tail && tail->next) {

tail = tail->next;

++l;

}

ListNode* next = tail->next;

if (l % 2 == 0) {

tail->next = nullptr;

prev->next = reverse(head);

head->next = next;

prev = head;

head = head->next;

} else {

prev = tail;

head = next;

}

return dummy.next;

}

};

花花酱 LeetCode 2073. Time Needed to Buy Tickets

By zxi on November 15, 2021

There are n people in a line queuing to buy tickets, where the 0^th person is at the front of the line and the (n - 1)^th person is at the back of the line.

You are given a 0-indexed integer array tickets of length n where the number of tickets that the i^th person would like to buy is tickets[i].

Each person takes exactly 1 second to buy a ticket. A person can only buy 1 ticket at a time and has to go back to the end of the line (which happens instantaneously) in order to buy more tickets. If a person does not have any tickets left to buy, the person will leave the line.

Return the time taken for the person at position k(0-indexed) to finish buying tickets.

Example 1:

Input: tickets = [2,3,2], k = 2
Output: 6
Explanation: 
- In the first pass, everyone in the line buys a ticket and the line becomes [1, 2, 1].
- In the second pass, everyone in the line buys a ticket and the line becomes [0, 1, 0].
The person at position 2 has successfully bought 2 tickets and it took 3 + 3 = 6 seconds.

Example 2:

Input: tickets = [5,1,1,1], k = 0
Output: 8
Explanation:
- In the first pass, everyone in the line buys a ticket and the line becomes [4, 0, 0, 0].
- In the next 4 passes, only the person in position 0 is buying tickets.
The person at position 0 has successfully bought 5 tickets and it took 4 + 1 + 1 + 1 + 1 = 8 seconds.

Constraints:

n == tickets.length
1 <= n <= 100
1 <= tickets[i] <= 100
0 <= k < n

Solution 1: Simulation

Time complexity: O(n * tickets[k])
Space complexity: O(n) / O(1)

C++

// Author: huahua

class Solution {

public:

int timeRequiredToBuy(vector<int>& tickets, int k) {

const int n = tickets.size();

queue<pair<int, int>> q;

for (int i = 0; i < n; ++i)

q.emplace(i, tickets[i]);

int ans = 0;

while (!q.empty()) {

++ans;

auto [i, t] = q.front(); q.pop();

if (--t == 0 && k == i) return ans;

if (t) q.emplace(i, t);

}

return -1;

}

};

Solution 2: Math

Each person before k will have tickets[k] rounds, each person after k will have tickets[k] – 1 rounds.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: huahua

class Solution {

public:

int timeRequiredToBuy(vector<int>& tickets, int k) {

int ans = 0;

for (int i = 0; i < tickets.size(); ++i)

ans += min(tickets[i], tickets[k] - (i > k));

return ans;

}

};

花花酱 LeetCode 2071. Maximum Number of Tasks You Can Assign

By zxi on November 14, 2021

You have n tasks and m workers. Each task has a strength requirement stored in a 0-indexed integer array tasks, with the i^th task requiring tasks[i] strength to complete. The strength of each worker is stored in a 0-indexed integer array workers, with the j^th worker having workers[j] strength. Each worker can only be assigned to a single task and must have a strength greater than or equal to the task’s strength requirement (i.e., workers[j] >= tasks[i]).

Additionally, you have pills magical pills that will increase a worker’s strength by strength. You can decide which workers receive the magical pills, however, you may only give each worker at most one magical pill.

Given the 0-indexed integer arrays tasks and workers and the integers pills and strength, return the maximum number of tasks that can be completed.

Example 1:

Input: tasks = [3,2,1], workers = [0,3,3], pills = 1, strength = 1
Output: 3
Explanation:
We can assign the magical pill and tasks as follows:
- Give the magical pill to worker 0.
- Assign worker 0 to task 2 (0 + 1 >= 1)
- Assign worker 1 to task 1 (3 >= 2)
- Assign worker 2 to task 0 (3 >= 3)

Example 2:

Input: tasks = [5,4], workers = [0,0,0], pills = 1, strength = 5
Output: 1
Explanation:
We can assign the magical pill and tasks as follows:
- Give the magical pill to worker 0.
- Assign worker 0 to task 0 (0 + 5 >= 5)

Example 3:

Input: tasks = [10,15,30], workers = [0,10,10,10,10], pills = 3, strength = 10
Output: 2
Explanation:
We can assign the magical pills and tasks as follows:
- Give the magical pill to worker 0 and worker 1.
- Assign worker 0 to task 0 (0 + 10 >= 10)
- Assign worker 1 to task 1 (10 + 10 >= 15)

Example 4:

Input: tasks = [5,9,8,5,9], workers = [1,6,4,2,6], pills = 1, strength = 5
Output: 3
Explanation:
We can assign the magical pill and tasks as follows:
- Give the magical pill to worker 2.
- Assign worker 1 to task 0 (6 >= 5)
- Assign worker 2 to task 2 (4 + 5 >= 8)
- Assign worker 4 to task 3 (6 >= 5)

Constraints:

n == tasks.length
m == workers.length
1 <= n, m <= 5 * 10⁴
0 <= pills <= m
0 <= tasks[i], workers[j], strength <= 10⁹

Solution: Greedy + Binary Search in Binary Search.

Find the smallest k, s.t. we are NOT able to assign. Then answer is k- 1.

The key is to verify whether we can assign k tasks or not.

Greedy: We want k smallest tasks and k strongest workers.

Start with the hardest tasks among (smallest) k:
1. assign task[i] to the weakest worker without a pill (if he can handle the hardest work so far, then the stronger workers can handle any simpler tasks left)
2. If 1) is not possible, we find a weakest worker + pill that can handle task[i] (otherwise we are wasting workers)
3. If 2) is not possible, impossible to finish k tasks.

Let k = min(n, m)
Time complexity: O((logk)² * k)
Space complexity: O(k)

C++

// Author: Huahua

class Solution {

public:

int maxTaskAssign(vector<int>& tasks, vector<int>& workers, int pills, int strength) {

const int n = tasks.size();

sort(begin(tasks), end(tasks));

sort(begin(workers), end(workers));

auto check = [&](int k) {

multiset<int> ws(rbegin(workers), rbegin(workers) + k);

for (int i = k - 1, p = 0; i >= 0; --i) {

auto it = ws.lower_bound(tasks[i]);

if (it != end(ws)) {

ws.erase(it);

} else if ((it = ws.lower_bound(tasks[i] - strength)) != end(ws)) {

if (++p > pills) return false;

ws.erase(it);

} else {

return false;

}

return true;

};

int l = 0;

int r = min(tasks.size(), workers.size()) + 1;

while (l < r) {

int m = l + (r - l) / 2;

if (!check(m)) {

r = m;

} else {

l = m + 1;

}

return l - 1;

}

};

花花酱 LeetCode 2070. Most Beautiful Item for Each Query

By zxi on November 14, 2021

You are given a 2D integer array items where items[i] = [price_i, beauty_i] denotes the price and beauty of an item respectively.

You are also given a 0-indexed integer array queries. For each queries[j], you want to determine the maximum beauty of an item whose price is less than or equal to queries[j]. If no such item exists, then the answer to this query is 0.

Return an array answer of the same length as queries where answer[j] is the answer to the j^th query.

Example 1:

Input: items = [[1,2],[3,2],[2,4],[5,6],[3,5]], queries = [1,2,3,4,5,6]
Output: [2,4,5,5,6,6]
Explanation:
- For queries[0]=1, [1,2] is the only item which has price <= 1. Hence, the answer for this query is 2.
- For queries[1]=2, the items which can be considered are [1,2] and [2,4]. 
  The maximum beauty among them is 4.
- For queries[2]=3 and queries[3]=4, the items which can be considered are [1,2], [3,2], [2,4], and [3,5].
  The maximum beauty among them is 5.
- For queries[4]=5 and queries[5]=6, all items can be considered.
  Hence, the answer for them is the maximum beauty of all items, i.e., 6.

Example 2:

Input: items = [[1,2],[1,2],[1,3],[1,4]], queries = [1]
Output: [4]
Explanation: 
The price of every item is equal to 1, so we choose the item with the maximum beauty 4. 
Note that multiple items can have the same price and/or beauty.

Example 3:

Input: items = [[10,1000]], queries = [5]
Output: [0]
Explanation:
No item has a price less than or equal to 5, so no item can be chosen.
Hence, the answer to the query is 0.

Constraints:

1 <= items.length, queries.length <= 10⁵
items[i].length == 2
1 <= price_i, beauty_i, queries[j] <= 10⁹

Solution: Prefix Max + Binary Search

Sort items by price. For each price, use a treemap to store the max beauty of an item whose prices is <= p. Then use binary search to find the max beauty whose price is <= p.

Time complexity: Pre-processing O(nlogn) + query: O(qlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {

sort(begin(items), end(items));

map<int, int> m;

int best = 0;

for (const auto& item : items) {

best = max(best, item[1]);

m[item[0]] = best;

}

vector<int> ans;

for (const int q: queries) {

auto it = m.upper_bound(q);

if (it == begin(m))

ans.push_back(0);

else

ans.push_back(prev(it)->second);

}

return ans;

}

};

花花酱 LeetCode 2069. Walking Robot Simulation II

By zxi on November 13, 2021

A width x height grid is on an XY-plane with the bottom-left cell at (0, 0) and the top-right cell at (width - 1, height - 1). The grid is aligned with the four cardinal directions ("North", "East", "South", and "West"). A robot is initially at cell (0, 0) facing direction "East".

The robot can be instructed to move for a specific number of steps. For each step, it does the following.

Attempts to move forward one cell in the direction it is facing.
If the cell the robot is moving to is out of bounds, the robot instead turns 90 degrees counterclockwise and retries the step.

After the robot finishes moving the number of steps required, it stops and awaits the next instruction.

Implement the Robot class:

Robot(int width, int height) Initializes the width x height grid with the robot at (0, 0) facing "East".
void move(int num) Instructs the robot to move forward num steps.
int[] getPos() Returns the current cell the robot is at, as an array of length 2, [x, y].
String getDir() Returns the current direction of the robot, "North", "East", "South", or "West".

Example 1:

Input
["Robot", "move", "move", "getPos", "getDir", "move", "move", "move", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
Output
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]

Explanation
Robot robot = new Robot(6, 3); // Initialize the grid and the robot at (0, 0) facing East.
robot.move(2);  // It moves two steps East to (2, 0), and faces East.
robot.move(2);  // It moves two steps East to (4, 0), and faces East.
robot.getPos(); // return [4, 0]
robot.getDir(); // return "East"
robot.move(2);  // It moves one step East to (5, 0), and faces East.
                // Moving the next step East would be out of bounds, so it turns and faces North.
                // Then, it moves one step North to (5, 1), and faces North.
robot.move(1);  // It moves one step North to (5, 2), and faces North (not West).
robot.move(4);  // Moving the next step North would be out of bounds, so it turns and faces West.
                // Then, it moves four steps West to (1, 2), and faces West.
robot.getPos(); // return [1, 2]
robot.getDir(); // return "West"

Constraints:

2 <= width, height <= 100
1 <= num <= 10⁵
At most 10⁴ calls in total will be made to move, getPos, and getDir.

Solution: Simulation

Note num >> w + h, when we hit a wall, we will always follow the boundary afterwards. We can do num %= p to reduce steps, where p = ((w – 1) + (h – 1)) * 2

Time complexity: move: O(min(num, w+h))
Space complexity: O(1)

C++

// Author: Huahua

constexpr static int dirs[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

const static vector<string> kNames{"East", "North", "West", "South"};

class Robot {

public:

Robot(int width, int height): w_(width), h_(height) {

p_ = ((w_ - 1) + (h_ - 1)) * 2;

}

void move(int num) {

while (num) {

int tx = x_ + dirs[d_][0];

int ty = y_ + dirs[d_][1];

if (tx < 0 || tx >= w_ || ty < 0 || ty >= h_) {

if (num > p_) num %= p_;

if (num) d_ = (d_ + 1) % 4;

continue;

}

x_ = tx;

y_ = ty;

--num;

}

vector<int> getPos() { return {x_, y_}; }

string getDir() { return kNames[d_]; }

private:

int w_;

int h_;

int d_{0}; // 0: E, 1: N, 2: W, 3: S

int x_{0};

int y_{0};

int p_{0};

};

Huahua's Tech Road

花花酱 LeetCode 2074. Reverse Nodes in Even Length Groups

Solution: List

C++

花花酱 LeetCode 2073. Time Needed to Buy Tickets

Solution 1: Simulation

C++

Solution 2: Math

C++

花花酱 LeetCode 2071. Maximum Number of Tasks You Can Assign

Solution: Greedy + Binary Search in Binary Search.

C++

花花酱 LeetCode 2070. Most Beautiful Item for Each Query

Solution: Prefix Max + Binary Search

C++

花花酱 LeetCode 2069. Walking Robot Simulation II

Solution: Simulation

C++