Huahua’s Tech Road

花花酱 LeetCode 1786. Number of Restricted Paths From First to Last Node

By zxi on March 6, 2021

There is an undirected weighted connected graph. You are given a positive integer n which denotes that the graph has n nodes labeled from 1 to n, and an array edges where each edges[i] = [u_i, v_i, weight_i] denotes that there is an edge between nodes u_i and v_i with weight equal to weight_i.

A path from node start to node end is a sequence of nodes [z₀, z₁,z₂, ..., z_k] such that z₀= start and z_k = end and there is an edge between z_i and z_i+1 where 0 <= i <= k-1.

The distance of a path is the sum of the weights on the edges of the path. Let distanceToLastNode(x) denote the shortest distance of a path between node n and node x. A restricted path is a path that also satisfies that distanceToLastNode(z_i) > distanceToLastNode(z_i+1) where 0 <= i <= k-1.

Return the number of restricted paths from node 1 to node n. Since that number may be too large, return it modulo 10⁹ + 7.

Example 1:

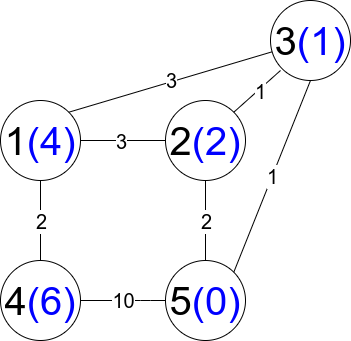
Input: n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output: 3
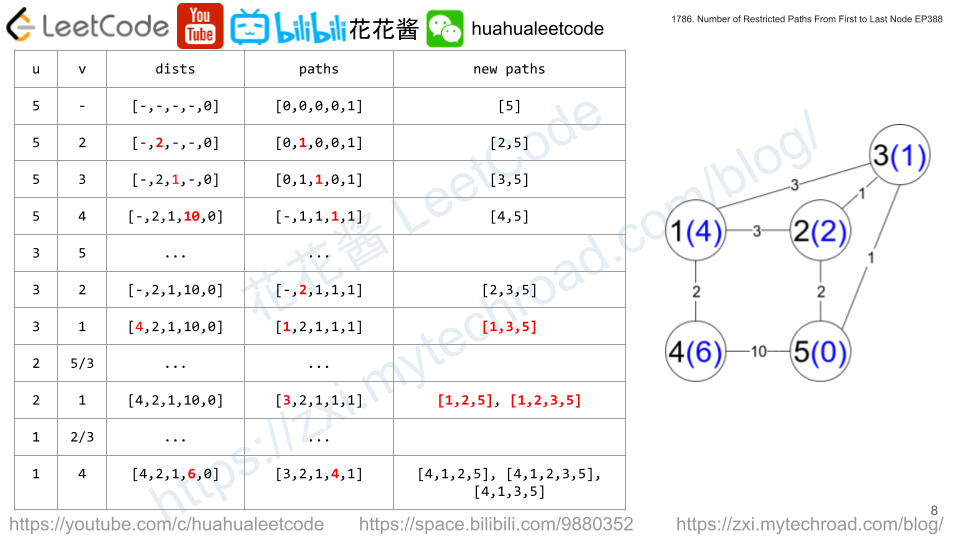
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

Example 2:

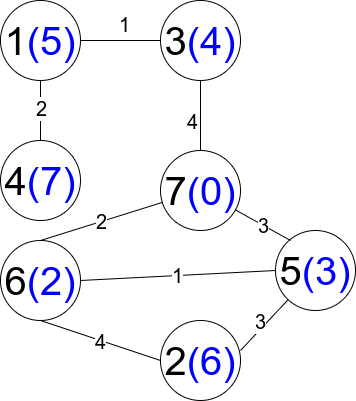
Input: n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output: 1
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The only restricted path is 1 --> 3 --> 7.

Constraints:

1 <= n <= 2 * 10⁴
n - 1 <= edges.length <= 4 * 10⁴
edges[i].length == 3
1 <= u_i, v_i <= n
u_i!= v_i
1 <= weight_i <= 10⁵
There is at most one edge between any two nodes.
There is at least one path between any two nodes.

Solution: Dijkstra + DFS w/ memoization

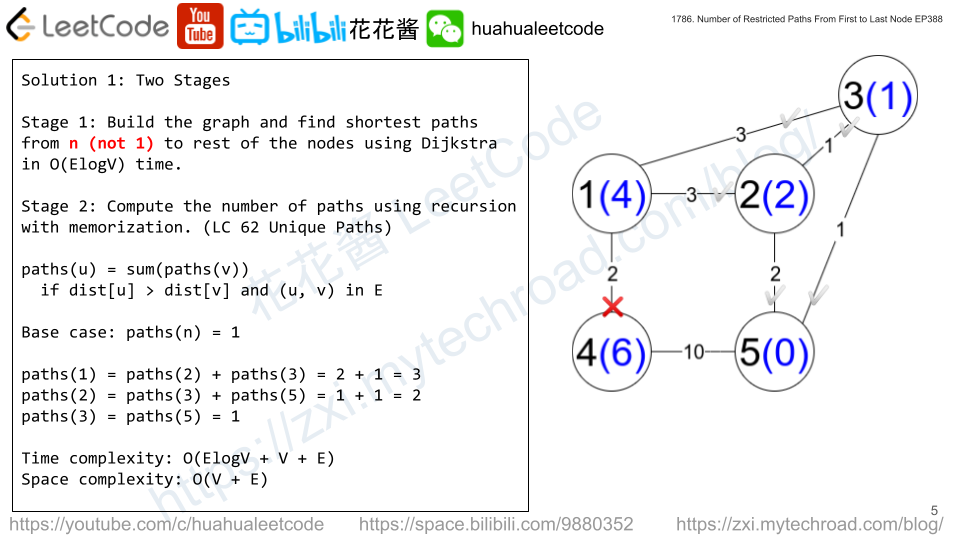
Find shortest path from n to all the nodes.
paths(u) = sum(paths(v)) if dist[u] > dist[v] and (u, v) has an edge
return paths(1)

Time complexity: O(ElogV + V + E)
Space complexity: O(V + E)

C++

// Author: Huahua

class Solution {

public:

int countRestrictedPaths(int n, vector<vector<int>>& edges) {

constexpr int kMod = 1e9 + 7;

using PII = pair<int, int>;

vector<vector<PII>> g(n + 1);

for (const auto& e : edges) {

g[e[0]].emplace_back(e[1], e[2]);

g[e[1]].emplace_back(e[0], e[2]);

}

// Shortest distance from n to x.

vector<int> dist(n + 1, INT_MAX / 2);

dist[n] = 0;

priority_queue<PII, vector<PII>, std::greater<PII>> q;

q.emplace(0, n);

while (!q.empty()) {

const auto [d, u] = q.top(); q.pop();

if (dist[u] < d) continue;

for (auto [v, w]: g[u]) {

if (dist[u] + w >= dist[v]) continue;

dist[v] = dist[u] + w;

q.emplace(dist[v], v);

}

vector<int> dp(n + 1, INT_MAX);

function<int(int)> dfs = [&](int u) {

if (u == n) return 1;

if (dp[u] != INT_MAX) return dp[u];

int ans = 0;

for (auto [v, w]: g[u])

if (dist[u] > dist[v])

ans = (ans + dfs(v)) % kMod;

return dp[u] = ans;

};

return dfs(1);

}

};

Combined

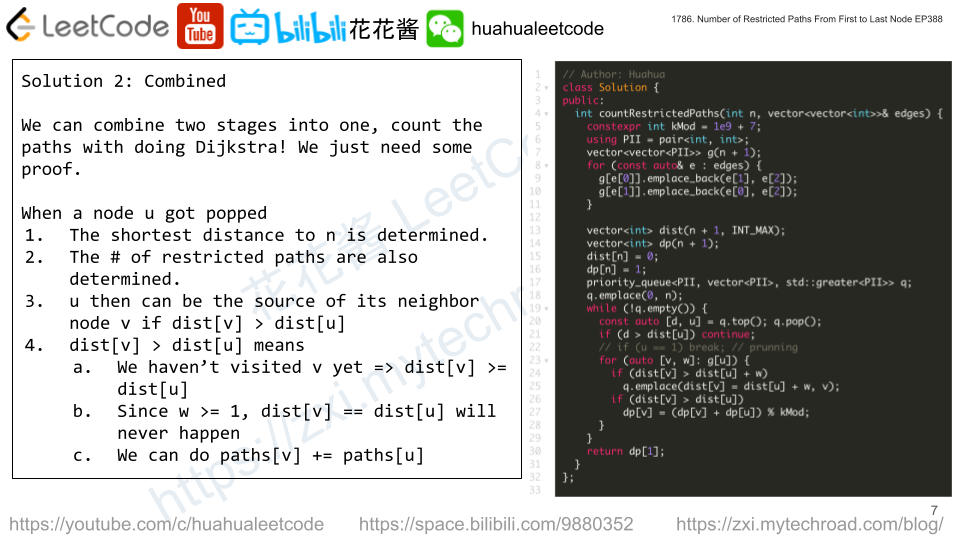
C++

// Author: Huahua

class Solution {

public:

int countRestrictedPaths(int n, vector<vector<int>>& edges) {

constexpr int kMod = 1e9 + 7;

using PII = pair<int, int>;

vector<vector<PII>> g(n + 1);

for (const auto& e : edges) {

g[e[0]].emplace_back(e[1], e[2]);

g[e[1]].emplace_back(e[0], e[2]);

}

// Shortest distance from n to x.

vector<int> dist(n + 1, INT_MAX);

vector<int> dp(n + 1);

dist[n] = 0;

dp[n] = 1;

priority_queue<PII, vector<PII>, std::greater<PII>> q;

q.emplace(0, n);

while (!q.empty()) {

const auto [d, u] = q.top(); q.pop();

if (d > dist[u]) continue;

if (u == 1) break;

for (auto [v, w]: g[u]) {

if (dist[v] > dist[u] + w)

q.emplace(dist[v] = dist[u] + w, v);

if (dist[v] > dist[u])

dp[v] = (dp[v] + dp[u]) % kMod;

}

return dp[1];

}

};

花花酱 LeetCode 1785. Minimum Elements to Add to Form a Given Sum

By zxi on March 6, 2021

You are given an integer array nums and two integers limit and goal. The array nums has an interesting property that abs(nums[i]) <= limit.

Return the minimum number of elements you need to add to make the sum of the array equal to goal. The array must maintain its property that abs(nums[i]) <= limit.

Note that abs(x) equals x if x >= 0, and -x otherwise.

Example 1:

Input: nums = [1,-1,1], limit = 3, goal = -4
Output: 2
Explanation: You can add -2 and -3, then the sum of the array will be 1 - 1 + 1 - 2 - 3 = -4.

Example 2:

Input: nums = [1,-10,9,1], limit = 100, goal = 0
Output: 1

Constraints:

1 <= nums.length <= 10⁵
1 <= limit <= 10⁶
-limit <= nums[i] <= limit
-10⁹ <= goal <= 10⁹

Solution: Math

Time complexity: O(n)
Space complexity: O(1)

Compute the diff = abs(sum(nums) – goal)
ans = （diff + limit – 1)) / limit

C++

// Author: Huahua

class Solution {

public:

int minElements(vector<int>& nums, int limit, int goal) {

int64_t diff = abs(goal -

accumulate(begin(nums), end(nums), 0LL));

return (diff + limit - 1) / limit;

}

};

花花酱 LeetCode 1784. Check if Binary String Has at Most One Segment of Ones

By zxi on March 6, 2021

Given a binary string s without leading zeros, return true if s contains at most one contiguous segment of ones. Otherwise, return false.

Example 1:

Input: s = "1001"
Output: false
Explanation: The ones do not form a contiguous segment.

Example 2:

Input: s = "110"
Output: true

Constraints:

1 <= s.length <= 100
s[i] is either '0' or '1'.
s[0] is '1'.

Solution: Counting

increase counter if s[i] == ‘1’ otherwise, reset counter.
increase counts when counter becomes 1.
return counts == 1

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool checkOnesSegment(string s) {

int count = 0;

int ones = 0;

for (const char c : s) {

if (c == '1') {

count += (++ones == 1);

} else {

ones = 0;

}

return count == 1;

}

};

花花酱 LeetCode 1782. Count Pairs Of Nodes

By zxi on March 6, 2021

You are given an undirected graph represented by an integer n, which is the number of nodes, and edges, where edges[i] = [u_i, v_i] which indicates that there is an undirected edge between u_i and v_i. You are also given an integer array queries.

The answer to the j^th query is the number of pairs of nodes (a, b) that satisfy the following conditions:

a < b
cnt is strictly greater than queries[j], where cnt is the number of edges incident to a or b.

Return an array answers such that answers.length == queries.length and answers[j] is the answer of the j^th query.

Note that there can be repeated edges.

Example 1:

Input: n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
Output: [6,5]
Explanation: The number of edges incident to at least one of each pair is shown above.

Example 2:

Input: n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
Output: [10,10,9,8,6]

Constraints:

2 <= n <= 2 * 10⁴
1 <= edges.length <= 10⁵
1 <= u_i, v_i <= n
u_i!= v_i
1 <= queries.length <= 20
0 <= queries[j] < edges.length

Solution 1: Pre-compute

Pre-compute # of pairs with total edges >= k. where k is from 0 to max_degree * 2 + 1.

Time complexity: (|node_degrees|² + V + E)
Space complexity: O(V+E)

C++

// Author: huahua

class Solution {

public:

vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) {

vector<int> node_degrees(n);

unordered_map<int, int> edge_freq;

for (auto& e : edges) {

sort(begin(e), end(e));

++node_degrees[--e[0]];

++node_degrees[--e[1]];

++edge_freq[(e[0] << 16) | e[1]];

}

const int max_degree = *max_element(begin(node_degrees),

end(node_degrees));

// Need pad one more to handle "not found / 0" case.

vector<int> counts(max_degree * 2 + 2);

unordered_map<int, int> degree_count;

for (int i = 0; i < n; ++i)

++degree_count[node_degrees[i]];

for (auto& [d1, c1] : degree_count)

for (auto& [d2, c2] : degree_count)

// Only count once if degrees are different to ensure (a < b)

if (d1 < d2) counts[d1 + d2] += c1 * c2;

// If degrees are the same C(n, 2) to ensure (a < b)

else if (d1 == d2) counts[d1 * 2] += c1 * (c1 - 1) / 2;

for (auto& [key, freq] : edge_freq) {

const int u = key >> 16;

const int v = key & 0xFFFF;

// For a pair of (u, v) their actual edge count is

// d[u] + d[v] - freq[(u, v)] instead of d[u] + d[v]

counts[node_degrees[u] + node_degrees[v]] -= 1;

counts[node_degrees[u] + node_degrees[v] - freq] += 1;

}

// counts[i] = # of pairs whose total edges >= i

for (int i = counts.size() - 2; i >= 0; --i)

counts[i] += counts[i + 1];

vector<int> ans;

for (int q : queries)

ans.push_back(counts[min(q + 1, static_cast<int>(counts.size() - 1))]);

return ans;

}

};

花花酱 LeetCode 1781. Sum of Beauty of All Substrings

By zxi on March 6, 2021

The beauty of a string is the difference in frequencies between the most frequent and least frequent characters.

For example, the beauty of "abaacc" is 3 - 1 = 2.

Given a string s, return the sum of beauty of all of its substrings.

Example 1:

Input: s = "aabcb"
Output: 5
Explanation: The substrings with non-zero beauty are ["aab","aabc","aabcb","abcb","bcb"], each with beauty equal to 1.

Example 2:

Input: s = "aabcbaa"
Output: 17

Constraints:

1 <= s.length <=500
s consists of only lowercase English letters.

Solution: Treemap

Time complexity: O(n²log26)
Space complexity: O(26)

C++

// Author: Huahua

class Solution {

public:

int beautySum(string_view s) {

const int n = s.size();

int ans = 0;

vector<int> f(26);

map<int, int> m;

for (int i = 0; i < n; ++i) {

fill(begin(f), end(f), 0);

m.clear();

for (int j = i; j < n; ++j) {

const int c = ++f[s[j] - 'a'];

++m[c];

if (c > 1) {

auto it = m.find(c - 1);

if (--it->second == 0)

m.erase(it);

}

ans += rbegin(m)->first - begin(m)->first;

}

return ans;

}

};

Huahua's Tech Road

花花酱 LeetCode 1786. Number of Restricted Paths From First to Last Node

Solution: Dijkstra + DFS w/ memoization

C++

C++

花花酱 LeetCode 1785. Minimum Elements to Add to Form a Given Sum

Solution: Math

C++

花花酱 LeetCode 1784. Check if Binary String Has at Most One Segment of Ones

Solution: Counting

C++

花花酱 LeetCode 1782. Count Pairs Of Nodes

Solution 1: Pre-compute

C++

花花酱 LeetCode 1781. Sum of Beauty of All Substrings

Solution: Treemap

C++