花花酱 LeetCode 1606. Find Servers That Handled Most Number of Requests

You have k servers numbered from 0 to k-1 that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but cannot handle more than one request at a time. The requests are assigned to servers according to a specific algorithm:

• The ith (0-indexed) request arrives.
• If all servers are busy, the request is dropped (not handled at all).
• If the (i % k)th server is available, assign the request to that server.
• Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the ith server is busy, try to assign the request to the (i+1)th server, then the (i+2)th server, and so on.

You are given a strictly increasing array arrival of positive integers, where arrival[i] represents the arrival time of the ith request, and another array load, where load[i] represents the load of the ith request (the time it takes to complete). Your goal is to find the busiest server(s). A server is considered busiest if it handled the most number of requests successfully among all the servers.

Return a list containing the IDs (0-indexed) of the busiest server(s). You may return the IDs in any order.

Example 1:

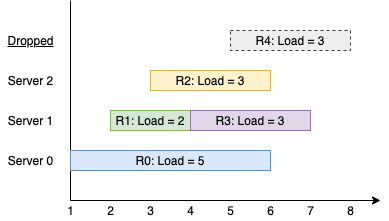
Input: k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3] 
Output: [1] 
Explanation:
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.

Example 2:

Input: k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
Output: [0]
Explanation:
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.

Example 3:

Input: k = 3, arrival = [1,2,3], load = [10,12,11]
Output: [0,1,2]
Explanation: Each server handles a single request, so they are all considered the busiest.

Example 4:

Input: k = 3, arrival = [1,2,3,4,8,9,10], load = [5,2,10,3,1,2,2]
Output: [1]

Example 5:

Input: k = 1, arrival = [1], load = [1]
Output: [0]

Constraints:

• 1 <= k <= 105
• 1 <= arrival.length, load.length <= 105
• arrival.length == load.length
• 1 <= arrival[i], load[i] <= 109
• arrival is strictly increasing.

Solution: Heap + TreeSet

Use a min heap to store the release time -> server.
Use a treeset to track the current available servers.
For reach request, check whether servers can be released at that time.

Time complexity: O(nlogk)
Space complexity: O(k)