Given a binary array nums, you should delete one element from it.
Return the size of the longest non-empty subarray containing only 1’s in the resulting array.
Return 0 if there is no such subarray.
Example 1:
Input: nums = [1,1,0,1] Output: 3 Explanation: After deleting the number in position 2, [1,1,1] contains 3 numbers with value of 1's.
Example 2:
Input: nums = [0,1,1,1,0,1,1,0,1] Output: 5 Explanation: After deleting the number in position 4, [0,1,1,1,1,1,0,1] longest subarray with value of 1's is [1,1,1,1,1].
Example 3:
Input: nums = [1,1,1] Output: 2 Explanation: You must delete one element.
Example 4:
Input: nums = [1,1,0,0,1,1,1,0,1] Output: 4
Example 5:
Input: nums = [0,0,0] Output: 0
Constraints:
1 <= nums.length <= 10^5nums[i]is either0or1.
Solution 1: DP
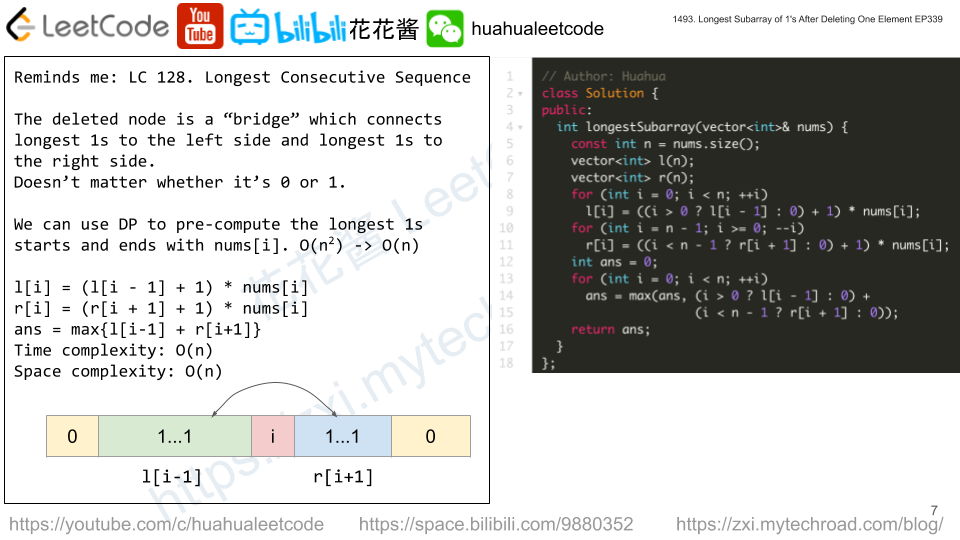
Preprocess:
l[i] := longest 1s from left side ends with nums[i], l[i] = nums[i] + nums[i] * l[i – 1]
r[i] := longest 1s from right side ends with nums[i], r[i] = nums[i] + nums[i] * r[i + 1]
Use each node as a bridge (ignored), the total number of consecutive 1s = l[i – 1] + r[i + 1].
ans = max{l[i-1] + r[i +1]}
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// Author: Huahua class Solution { public: int longestSubarray(vector<int>& nums) { const int n = nums.size(); vector<int> l(n); vector<int> r(n); for (int i = 0; i < n; ++i) l[i] = (i > 0 ? l[i - 1] * nums[i] : 0) + nums[i]; for (int i = n - 1; i >= 0; --i) r[i] = (i < n - 1 ? r[i + 1] * nums[i] : 0) + nums[i]; int ans = 0; for (int i = 0; i < n; ++i) ans = max(ans, (i > 0 ? l[i - 1] : 0) + (i < n - 1 ? r[i + 1] : 0)); return ans; } }; |
Solution 2: DP
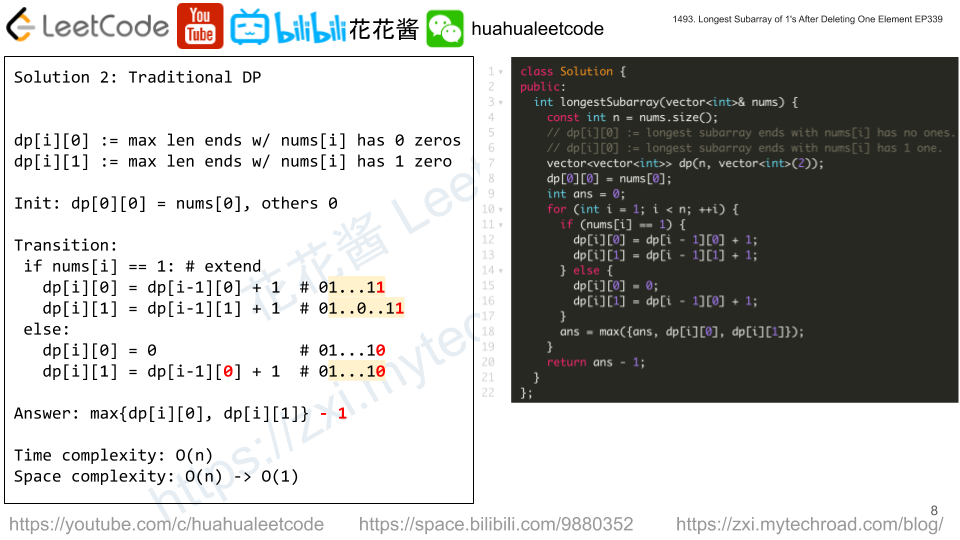
dp[i][0] := longest subarray ends with nums[i] has no ones.
dp[i][0] := longest subarray ends with nums[i] has 1 one.
if nums[i] == 1:
dp[i][0] = dp[i – 1][0] + 1
dp[i][1] = dp[i – 1][1] + 1
if nums[i] == 0:
dp[i][0] = 0
dp[i][1] = dp[i – 1][0] + 1
Time complexity: O(n)
Space complexity: O(n) -> O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
// Author: Huahua class Solution { public: int longestSubarray(vector<int>& nums) { const int n = nums.size(); // dp[i][0] := longest subarray ends with nums[i-1] has no zeros. // dp[i][0] := longest subarray ends with nums[i-1] has 1 zero. vector<vector<int>> dp(n + 1, vector<int>(2)); int ans = 0; for (int i = 1; i <= n; ++i) { if (nums[i - 1] == 1) { dp[i][0] = dp[i - 1][0] + 1; dp[i][1] = dp[i - 1][1] + 1; } else { dp[i][0] = 0; dp[i][1] = dp[i - 1][0] + 1; } ans = max({ans, dp[i][0] - 1, dp[i][1] - 1}); } return ans; } }; |
Solution 3: Sliding Window

Maintain a sliding window l ~ r s.t sum(num[l~r]) >= r – l. There can be at most one 0 in the window.
ans = max{r – l} for all valid windows.
Time complexity: O(n)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
// Author: Huahua class Solution { public: int longestSubarray(vector<int>& nums) { const int n = nums.size(); int ans = 0; int sum = 0; // sum of nums[l~r]. for (int l = 0, r = 0; r < n; ++r) { sum += nums[r]; // Maintain sum >= r - l, at most 1 zero. while (l < r && sum < r - l) sum -= nums[l++]; ans = max(ans, r - l); } return ans; } }; |