Posts tagged as “union find”

花花酱 LeetCode 959. Regions Cut By Slashes

By zxi on December 18, 2018

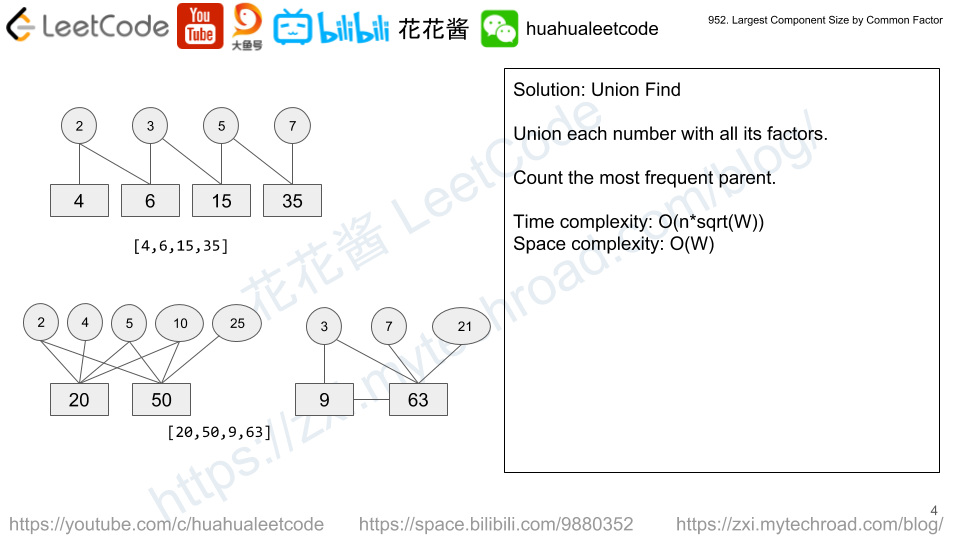
In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.

(Note that backslash characters are escaped, so a \ is represented as "\\".)

Return the number of regions.

Example 1:

Input:[  " /",  "/ "]
Output: 2
Explanation: The 2x2 grid is as follows:

Example 2:

Input:[  " /",  "  "]
Output: 1
Explanation: The 2x2 grid is as follows:

Example 3:

Input:[  "\\/",  "/\\"]
Output: 4
Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)The 2x2 grid is as follows:

Example 4:

Input:[  "/\\",  "\\/"]
Output: 5
Explanation: (Recall that because \ characters are escaped, "/\\" refers to /\, and "\\/" refers to \/.)The 2x2 grid is as follows:

Example 5:

Input:[  "//",  "/ "]
Output: 3
Explanation: The 2x2 grid is as follows:

Note:

1 <= grid.length == grid[0].length <= 30
grid[i][j] is either '/', '\', or ' '.

Solution 1: Split grid into 4 triangles and Union Find Faces

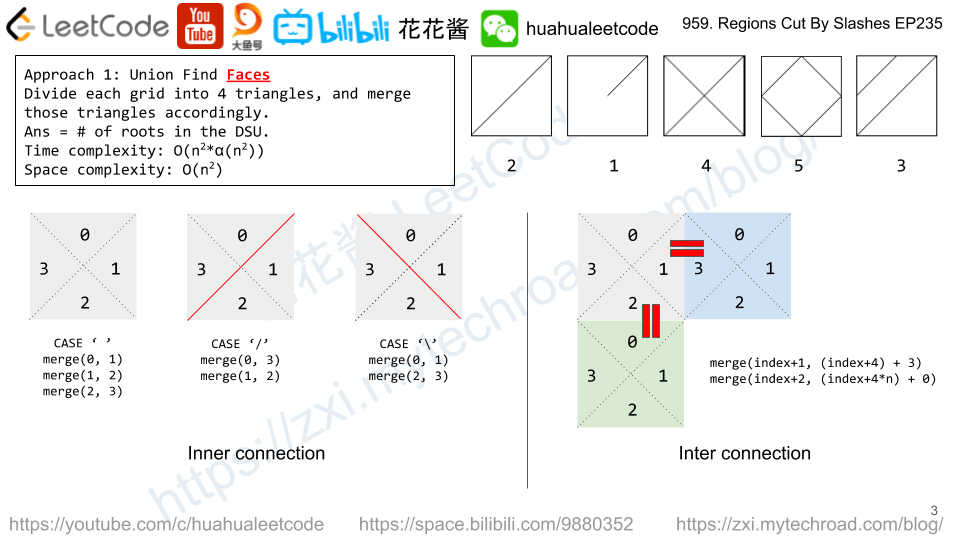
Divide each grid into 4 triangles and union them if not split.
Time complexity: O(n^2*alphn(n^2))
Space complexity: O(n^2)

C++

class Solution {

public:

int regionsBySlashes(vector<string>& grid) {

int n = grid.size();

DSU dsu(4 * n * n);

for (int r = 0; r < n; ++r)

for (int c = 0; c < n; ++c) {

int index = 4 * (r * n + c);

switch (grid[r][c]) {

case '/':

dsu.merge(index + 0, index + 3);

dsu.merge(index + 1, index + 2);

break;

case '\\':

dsu.merge(index + 0, index + 1);

dsu.merge(index + 2, index + 3);

break;

case ' ':

dsu.merge(index + 0, index + 1);

dsu.merge(index + 1, index + 2);

dsu.merge(index + 2, index + 3);

break;

default: break;

}

if (r + 1 < n)

dsu.merge(index + 2, index + 4 * n + 0);

if (c + 1 < n)

dsu.merge(index + 1, index + 4 + 3);

}

int ans = 0;

for (int i = 0; i < 4 * n * n; ++i)

if (dsu.find(i) == i) ++ans;

return ans;

}

private:

class DSU {

public:

DSU(int n): parent_(n) {

for (int i = 0; i < n; ++i)

parent_[i] = i;

}

int find(int x) {

if (parent_[x] != x) parent_[x] = find(parent_[x]);

return parent_[x];

}

void merge(int x, int y) {

parent_[find(x)] = find(y);

}

private:

vector<int> parent_;

};

Solution 2: Euler’s Formula / Union-Find vertices

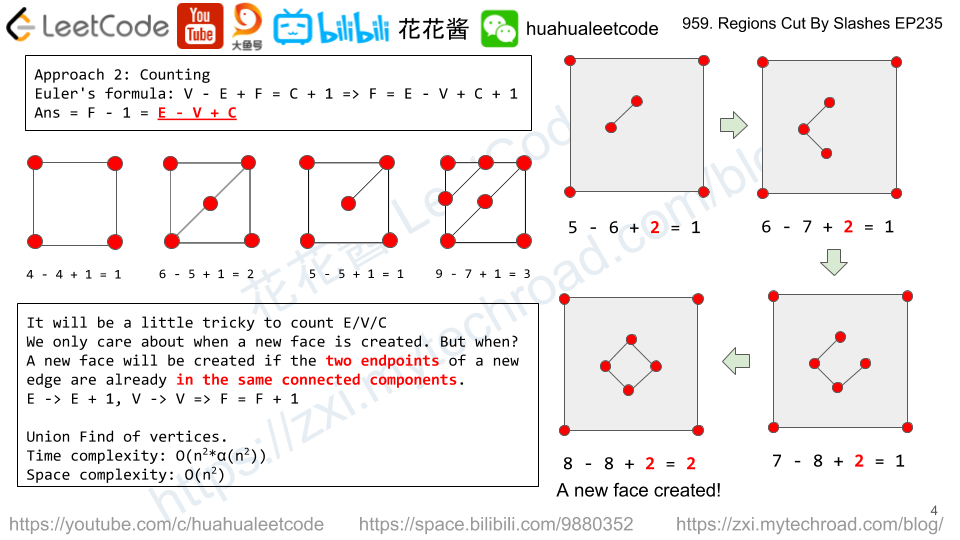
C++

class Solution {

public:

int regionsBySlashes(vector<string>& grid) {

int n = grid.size();

p_ = vector<int>((n + 1) * (n + 1));

// All vertices on the boundaries are merged into root(0).

for (int r = 0; r < n + 1; ++r)

for (int c = 0; c < n + 1; ++c)

p_[getIndex(n, r, c)] = (r == 0 || r == n || c == 0 || c == n) ? 0 : getIndex(n, r, c);

int f = 1;

for (int r = 0; r < n; ++r)

for (int c = 0; c < n; ++c) {

if (grid[r][c] == ' ') continue;

// A new face will created if two vertices are already in the same group.

if (grid[r][c] == '/') {

f += merge(getIndex(n, r, c + 1),

getIndex(n, r + 1, c));

} else {

f += merge(getIndex(n, r, c),

getIndex(n, r + 1, c + 1));

}

return f;

}

private:

vector<int> p_;

int getIndex(int n, int r, int c) { return r * (n + 1) + c; }

int find(int x) {

if (p_[x] != x) p_[x] = find(p_[x]);

return p_[x];

}

int merge(int x, int y) {

int rx = find(x);

int ry = find(y);

if (rx == ry) return 1;

p_[ry] = rx;

return 0;

}

};

Solution 3: Pixelation (Upscale 3 times)

Time complexity: O(n^2)
Space complexity: O(n^2)

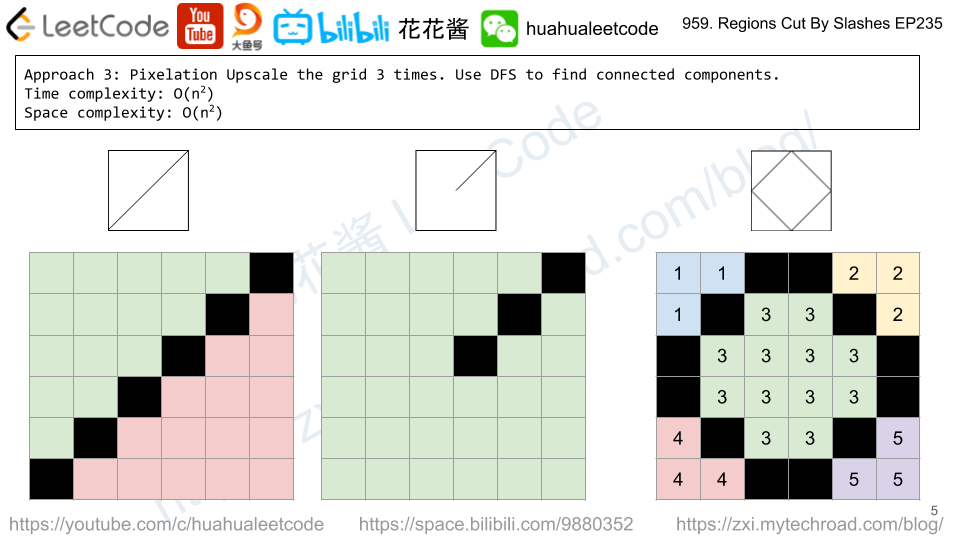
C++

// Author: Huahua, running time: 20 ms

class Solution {

public:

int regionsBySlashes(vector<string>& grid) {

const int n = grid.size();

vector<vector<int>> g(n * 3, vector<int>(n * 3));

for (int i = 0; i < n; ++i)

for (int j = 0; j < n; ++j) {

if (grid[i][j] == '/') {

g[i * 3 + 0][j * 3 + 2] = 1;

g[i * 3 + 1][j * 3 + 1] = 1;

g[i * 3 + 2][j * 3 + 0] = 1;

} else if (grid[i][j] == '\\') {

g[i * 3 + 0][j * 3 + 0] = 1;

g[i * 3 + 1][j * 3 + 1] = 1;

g[i * 3 + 2][j * 3 + 2] = 1;

}

int ans = 0;

for (int i = 0; i < 3 * n; ++i)

for (int j = 0; j < 3 * n; ++j) {

if (g[i][j]) continue;

visit(g, j, i, n * 3);

++ans;

}

return ans;

}

private:

void visit(vector<vector<int>>& g, int x, int y, int n) {

if (x < 0 || x >= n || y < 0 || y >= n) return;

if (g[y][x]) return;

g[y][x] = 1;

visit(g, x + 1, y, n);

visit(g, x, y + 1, n);

visit(g, x - 1, y, n);

visit(g, x, y - 1, n);

}

};

花花酱 LeetCode 952. Largest Component Size by Common Factor

By zxi on December 1, 2018

Problem

Given a non-empty array of unique positive integers A, consider the following graph:

There are A.length nodes, labelled A[0] to A[A.length - 1];
There is an edge between A[i] and A[j] if and only if A[i] and A[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

Example 1:

Input: [4,6,15,35]
Output: 4

Example 2:

Input: [20,50,9,63]
Output: 2

Example 3:

Input: [2,3,6,7,4,12,21,39]
Output: 8

Note:

1 <= A.length <= 20000
1 <= A[i] <= 100000

Solution: Union Find

For each number, union itself with all its factors.

E.g. 6, union(6,2), union(6,3)

Time complexity: \( O(\Sigma{sqrt(A[i])}) \)

Space complexity: \( O(max(A)) \)

C++

// Author: Huahua, running time: 148 ms

class DSU {

public:

DSU(int n): p_(n) {

for (int i = 0; i < n; ++i)

p_[i] = i;

}

void Union(int x, int y) {

p_[Find(x)] = p_[Find(y)];

}

int Find(int x) {

if (p_[x] != x) p_[x] = Find(p_[x]);

return p_[x];

}

private:

vector<int> p_;

};

class Solution {

public:

int largestComponentSize(vector<int>& A) {

int n = *max_element(begin(A), end(A));

DSU dsu(n + 1);

for (int a : A) {

int t = sqrt(a);

for (int k = 2; k <= t; ++k)

if (a % k == 0) {

dsu.Union(a, k);

dsu.Union(a, a / k);

}

unordered_map<int, int> c;

int ans = 1;

for (int a : A)

ans = max(ans, ++c[dsu.Find(a)]);

return ans;

}

};

Python3

# Author: Huahua, running time: 3432 ms

class Solution:

def largestComponentSize(self, A):

p = list(range(max(A) + 1))

def find(x):

while p[x] != x:

p[x] = p[p[x]]

x = p[x]

return x

def union(x, y):

p[find(x)] = p[find(y)]

for a in A:

for k in range(2, int(math.sqrt(a) + 1)):

if a % k == 0:

union(a, k)

union(a, a // k)

return collections.Counter([find(a) for a in A]).most_common(1)[0][1]

花花酱 LeetCode 947. Most Stones Removed with Same Row or Column

By zxi on November 29, 2018

Problem

On a 2D plane, we place stones at some integer coordinate points. Each coordinate point may have at most one stone.

Now, a move consists of removing a stone that shares a column or row with another stone on the grid.

What is the largest possible number of moves we can make?

Example 1:

Input: stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
Output: 5

Example 2:

Input: stones = [[0,0],[0,2],[1,1],[2,0],[2,2]]
Output: 3

Example 3:

Input: stones = [[0,0]]
Output: 0

Note:

1 <= stones.length <= 1000
0 <= stones[i][j] < 10000

Solution 2: Union Find

Find all connected components (islands)

Ans = # of stones – # of islands

C++

// Author: Huahua, running time: 16 ms

class Solution {

public:

int removeStones(vector<vector<int>>& stones) {

const int kSize = 10000;

DSU dsu(kSize * 2);

for (const auto& stone : stones)

dsu.Union(stone[0], stone[1] + kSize);

unordered_set<int> seen;

for (const auto& stone : stones)

seen.insert(dsu.Find(stone[0]));

return stones.size() - seen.size();

}

private:

class DSU {

public:

DSU(int n): p_(n) {

for (int i = 0 ; i < n; ++i)

p_[i] = i;

}

void Union(int i, int j) {

p_[Find(i)] = Find(j);

}

int Find(int i) {

if (p_[i] != i) p_[i] = Find(p_[i]);

return p_[i];

}

private:

vector<int> p_;

};

Problem

Two strings X and Y are similar if we can swap two letters (in different positions) of X, so that it equals Y.

For example, "tars" and "rats" are similar (swapping at positions 0 and 2), and "rats" and "arts" are similar, but "star" is not similar to "tars", "rats", or "arts".

Together, these form two connected groups by similarity: {"tars", "rats", "arts"} and {"star"}. Notice that "tars" and "arts" are in the same group even though they are not similar. Formally, each group is such that a word is in the group if and only if it is similar to at least one other word in the group.

We are given a list A of strings. Every string in A is an anagram of every other string in A. How many groups are there?

Example 1:

Input: ["tars","rats","arts","star"]
Output: 2

Note:

A.length <= 2000
A[i].length <= 1000
A.length * A[i].length <= 20000
All words in A consist of lowercase letters only.
All words in A have the same length and are anagrams of each other.
The judging time limit has been increased for this question.

Solution: Brute Force + Union Find

Time Complexity: O(n^2 * L)

Space Complexity: O(n)

C++

// Author: Huahua

// Running time: 230 ms (<99.08%)

class DSU {

public:

DSU(int size):size_(size), parent_(size), rank_(size) {

iota(begin(parent_), end(parent_), 0);

}

int Find(int n) {

if (parent_[n] != n)

parent_[n] = Find(parent_[n]);

return parent_[n];

}

void Union(int x, int y) {

int px = Find(x);

int py = Find(y);

if (px == py) return;

if (rank_[py] > rank_[px])

swap(px, py);

else if (rank_[py] == rank_[px])

++rank_[px];

parent_[py] = px;

--size_;

}

int Size() const {

return size_;

}

private:

int size_;

vector<int> ranks_;

vector<int> parent_;

};

class Solution {

public:

int numSimilarGroups(vector<string>& A) {

DSU dsu(A.size());

for (int i = 0; i < A.size(); ++i)

for (int j = i + 1; j < A.size(); ++j)

if (similar(A[i], A[j]))

dsu.Union(i, j);

return dsu.Size();

}

private:

bool similar(const string& a, const string& b) {

int diff = 0;

for (int i = 0; i < a.length(); ++i)

if (a[i] != b[i] && ++diff > 2) return false;

return true;

}

};

花花酱 LeetCode 399. Evaluate Division

By zxi on December 1, 2017

题目大意：给你一些含有变量名的分式的值，让你计算另外一些分式的值，如果不能计算返回-1。

Problem:

Equations are given in the format A / B = k, where A and B are variables represented as strings, and k is a real number (floating point number). Given some queries, return the answers. If the answer does not exist, return -1.0.

Example:
Given a / b = 2.0, b / c = 3.0.
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? .
return [6.0, 0.5, -1.0, 1.0, -1.0 ].

The input is: vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries , where equations.size() == values.size(), and the values are positive. This represents the equations. Return vector<double>.

According to the example above:

equations = [ ["a", "b"], ["b", "c"] ],

values = [2.0, 3.0],

queries = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ].

The input is always valid. You may assume that evaluating the queries will result in no division by zero and there is no contradiction.

Solution 1: DFS

C++

// Author: Huahua

// Runtime: 3 ms

class Solution {

public:

vector<double> calcEquation(vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries) {

// g[A][B] = k -> A / B = k

unordered_map<string, unordered_map<string, double>> g;

for (int i = 0; i < equations.size(); ++i) {

const string& A = equations[i].first;

const string& B = equations[i].second;

const double k = values[i];

g[A][B] = k;

g[B][A] = 1.0 / k;

}

vector<double> ans;

for (const auto& pair : queries) {

const string& X = pair.first;

const string& Y = pair.second;

if (!g.count(X) || !g.count(Y)) {

ans.push_back(-1.0);

continue;

}

unordered_set<string> visited;

ans.push_back(divide(X, Y, g, visited));

}

return ans;

}

private:

// get result of A / B

double divide(const string& A, const string& B,

unordered_map<string, unordered_map<string, double>>& g,

unordered_set<string>& visited) {

if (A == B) return 1.0;

visited.insert(A);

for (const auto& pair : g[A]) {

const string& C = pair.first;

if (visited.count(C)) continue;

double d = divide(C, B, g, visited); // d = C / B

// A / B = C / B * A / C

if (d > 0) return d * g[A][C];

}

return -1.0;

}

};

Java

// Updated: 2020/9/27

// Author: Huahua

// Running time: 1 ms

class Solution {

private Map<String, HashMap<String, Double>> g = new HashMap<>();

public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {

for (int i = 0; i < equations.size(); ++i) {

String x = equations.get(i).get(0);

String y = equations.get(i).get(1);

double k = values[i];

g.computeIfAbsent(x, l -> new HashMap<String, Double>()).put(y, k);

g.computeIfAbsent(y, l -> new HashMap<String, Double>()).put(x, 1.0 / k);

}

double[] ans = new double[queries.size()];

for (int i = 0; i < queries.size(); ++i) {

String x = queries.get(i).get(0);

String y = queries.get(i).get(1);

if (!g.containsKey(x) || !g.containsKey(y)) {

ans[i] = -1.0;

} else {

ans[i] = divide(x, y, new HashSet<String>());

}

return ans;

}

private double divide(String x, String y, Set<String> visited) {

if (x.equals(y)) return 1.0;

visited.add(x);

if (!g.containsKey(x)) return -1.0;

for (String n : g.get(x).keySet()) {

if (visited.contains(n)) continue;

visited.add(n);

double d = divide(n, y, visited);

if (d > 0) return d * g.get(x).get(n);

}

return -1.0;

}

Python3

"""

Author: Huahua

Running time: 32 ms (beats 100%)

"""

class Solution:

def calcEquation(self, equations, values, queries):

def divide(x, y, visited):

if x == y: return 1.0

visited.add(x)

for n in g[x]:

if n in visited: continue

visited.add(n)

d = divide(n, y, visited)

if d > 0: return d * g[x][n]

return -1.0

g = collections.defaultdict(dict)

for (x, y), v in zip(equations, values):

g[x][y] = v

g[y][x] = 1.0 / v

ans = [divide(x, y, set()) if x in g and y in g else -1 for x, y in queries]

return ans

Solution 2: Union Find

C++

// Author: Huahua

// Runtime: 3 ms

class Solution {

public:

vector<double> calcEquation(const vector<pair<string, string>>& equations, vector<double>& values, const vector<pair<string, string>>& queries) {

// parents["A"] = {"B", 2.0} -> A = 2.0 * B

// parents["B"] = {"C", 3.0} -> B = 3.0 * C

unordered_map<string, pair<string, double>> parents;

for (int i = 0; i < equations.size(); ++i) {

const string& A = equations[i].first;

const string& B = equations[i].second;

const double k = values[i];

// Neighter is in the forrest

if (!parents.count(A) && !parents.count(B)) {

parents[A] = {B, k};

parents[B] = {B, 1.0};

} else if (!parents.count(A)) {

parents[A] = {B, k};

} else if (!parents.count(B)) {

parents[B] = {A, 1.0 / k};

} else {

auto& rA = find(A, parents);

auto& rB = find(B, parents);

parents[rA.first] = {rB.first, k / rA.second * rB.second};

}

vector<double> ans;

for (const auto& pair : queries) {

const string& X = pair.first;

const string& Y = pair.second;

if (!parents.count(X) || !parents.count(Y)) {

ans.push_back(-1.0);

continue;

}

auto& rX = find(X, parents); // {rX, X / rX}

auto& rY = find(Y, parents); // {rY, Y / rY}

if (rX.first != rY.first)

ans.push_back(-1.0);

else // X / Y = (X / rX / (Y / rY))

ans.push_back(rX.second / rY.second);

}

return ans;

}

private:

pair<string, double>& find(const string& C, unordered_map<string, pair<string, double>>& parents) {

if (C != parents[C].first) {

const auto& p = find(parents[C].first, parents);

parents[C].first = p.first;

parents[C].second *= p.second;

}

return parents[C];

}

};

Java

// Updated: 9/27/2020

// Author: Huahua

// Running time: 3 ms

class Solution {

class Node {

public String parent;

public double ratio;

public Node(String parent, double ratio) {

this.parent = parent;

this.ratio = ratio;

}

class UnionFindSet {

private Map<String, Node> parents = new HashMap<>();

public Node find(String s) {

if (!parents.containsKey(s)) return null;

Node n = parents.get(s);

if (!n.parent.equals(s)) {

Node p = find(n.parent);

n.parent = p.parent;

n.ratio *= p.ratio;

}

return n;

}

public void union(String A, String B, double ratio) {

boolean hasA = parents.containsKey(A);

boolean hasB = parents.containsKey(B);

if (!hasA && !hasB) {

parents.put(A, new Node(B, ratio));

parents.put(B, new Node(B, 1.0));

} else if (!hasA) {

parents.put(A, new Node(B, ratio));

} else if (!hasB) {

parents.put(B, new Node(A, 1.0 / ratio));

} else {

Node rA = find(A);

Node rB = find(B);

parents.put(rA.parent,

new Node(rB.parent, ratio / rA.ratio * rB.ratio));

}

public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {

UnionFindSet u = new UnionFindSet();

for (int i = 0; i < equations.size(); ++i)

u.union(equations.get(i).get(0), equations.get(i).get(1), values[i]);

double[] ans = new double[queries.size()];

for (int i = 0; i < queries.size(); ++i) {

Node rx = u.find(queries.get(i).get(0));

Node ry = u.find(queries.get(i).get(1));

if (rx == null || ry == null || !rx.parent.equals(ry.parent))

ans[i] = -1.0;

else

ans[i] = rx.ratio / ry.ratio;

}

return ans;

}

Python3

"""

Author: Huahua

Running time: 32 ms (beats 100%)

"""

class Solution:

def calcEquation(self, equations, values, queries):

def find(x):

if x != U[x][0]:

px, pv = find(U[x][0])

U[x] = (px, U[x][1] * pv)

return U[x]

def divide(x, y):

rx, vx = find(x)

ry, vy = find(y)

if rx != ry: return -1.0

return vx / vy

U = {}

for (x, y), v in zip(equations, values):

if x not in U and y not in U:

U[x] = (y, v)

U[y] = (y, 1.0)

elif x not in U:

U[x] = (y, v)

elif y not in U:

U[y] = (x, 1.0 / v)

else:

rx, vx = find(x)

ry, vy = find(y)

U[rx] = (ry, v / vx * vy)

ans = [divide(x, y) if x in U and y in U else -1 for x, y in queries]

return ans

Related Problems:

Posts tagged as “union find”

花花酱 LeetCode 959. Regions Cut By Slashes

Solution 1: Split grid into 4 triangles and Union Find Faces

C++

Solution 2: Euler’s Formula / Union-Find vertices

C++

Solution 3: Pixelation (Upscale 3 times)

C++

花花酱 LeetCode 952. Largest Component Size by Common Factor

Problem

Solution: Union Find

C++

Python3

花花酱 LeetCode 947. Most Stones Removed with Same Row or Column

Problem

Solution 2: Union Find

C++

Related Problems

花花酱 LeetCode 839. Similar String Groups

Problem

Solution: Brute Force + Union Find

花花酱 LeetCode 399. Evaluate Division

Solution 1: DFS

C++

Java

Python3

Solution 2: Union Find

C++

Java

Python3