Posts published in “Tree”

花花酱 LeetCode 2196. Create Binary Tree From Descriptions

By zxi on March 8, 2022

You are given a 2D integer array descriptions where descriptions[i] = [parent_i, child_i, isLeft_i] indicates that parent_i is the parent of child_i in a binary tree of unique values. Furthermore,

If isLeft_i == 1, then child_i is the left child of parent_i.
If isLeft_i == 0, then child_i is the right child of parent_i.

Construct the binary tree described by descriptions and return its root.

The test cases will be generated such that the binary tree is valid.

Example 1:

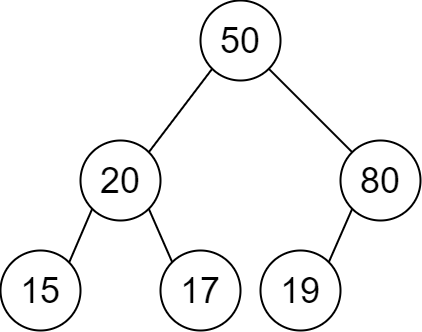
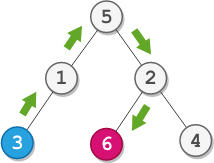
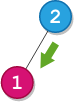
Input: descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
Output: [50,20,80,15,17,19]
Explanation: The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.

Example 2:

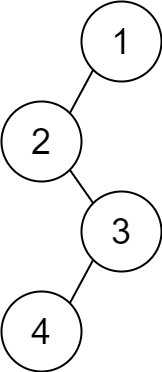
Input: descriptions = [[1,2,1],[2,3,0],[3,4,1]]
Output: [1,2,null,null,3,4]
Explanation: The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.

Constraints:

1 <= descriptions.length <= 10⁴
descriptions[i].length == 3
1 <= parent_i, child_i <= 10⁵
0 <= isLeft_i <= 1
The binary tree described by descriptions is valid.

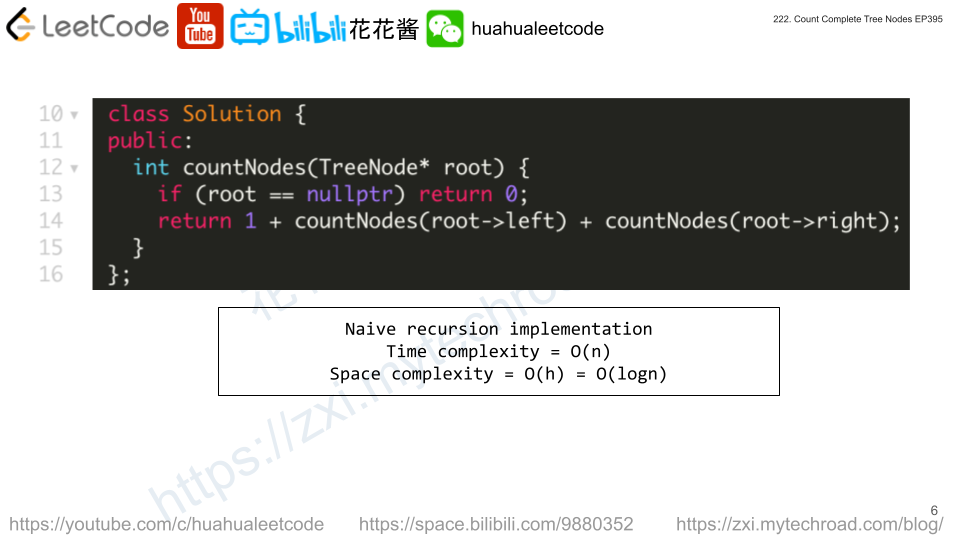
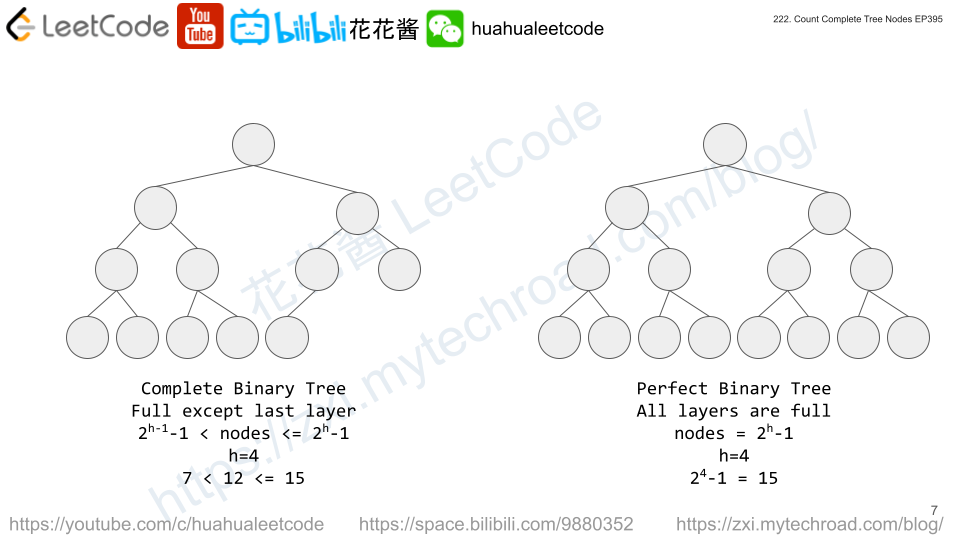
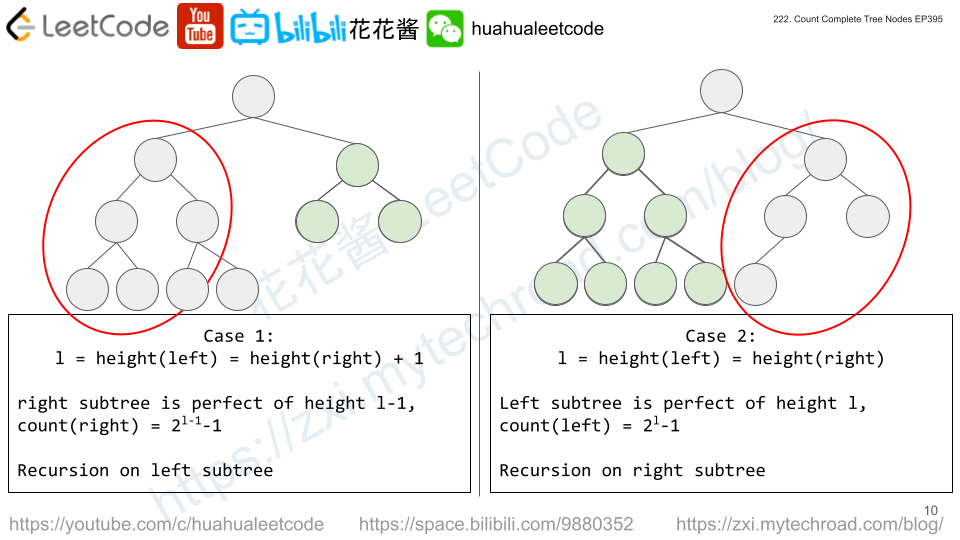
Solution: Hashtable + Recursion

Use one hashtable to track the children of each node.
Use another hashtable to track the parent of each node.
Find the root who doesn’t have parent.
Build the tree recursively from root.

Time complexity: O(n)
Space complexity: O(n)

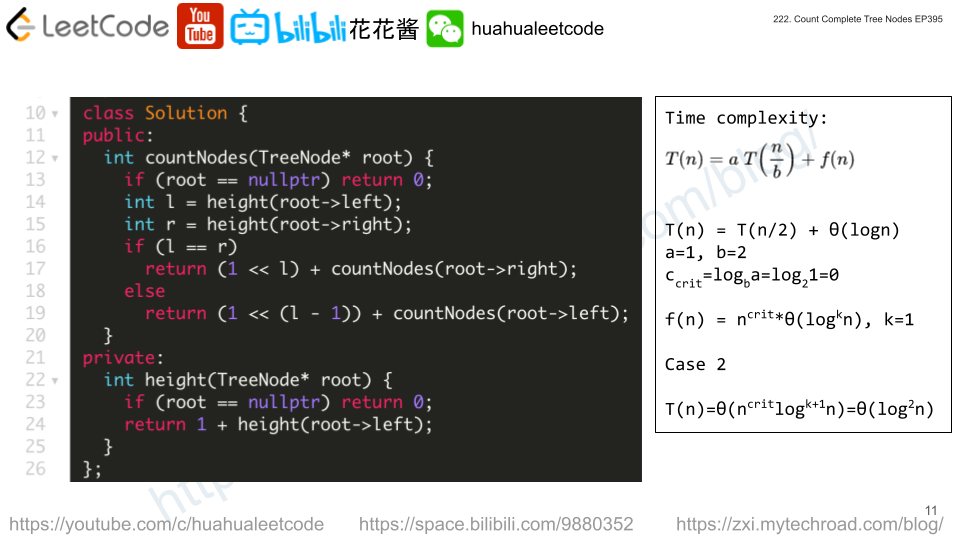
C++

// Author: Huahua

class Solution {

public:

TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {

unordered_set<int> hasParent;

unordered_map<int, pair<int, int>> children;

for (const auto& d : descriptions) {

hasParent.insert(d[1]);

(d[2] ? children[d[0]].first : children[d[0]].second) = d[1];

}

int root = -1;

for (const auto& d : descriptions)

if (!hasParent.count(d[0])) root = d[0];

function<TreeNode*(int)> build = [&](int cur) -> TreeNode* {

if (!cur) return nullptr;

return new TreeNode(cur,

build(children[cur].first),

build(children[cur].second));

};

return build(root);

}

};

花花酱 LeetCode 222. Count Complete Tree Nodes

By zxi on December 7, 2021

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2^h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

Example 1:

Input: root = [1,2,3,4,5,6]
Output: 6

Example 2:

Input: root = []
Output: 0

Example 3:

Input: root = [1]
Output: 1

Constraints:

The number of nodes in the tree is in the range [0, 5 * 10⁴].
0 <= Node.val <= 5 * 10⁴
The tree is guaranteed to be complete.

Solution: Recursion

For each node, count the height of it’s left and right subtree by going left only.

Let L = height(left) R = height(root), if L == R, which means the left subtree is perfect.
It has (2^L – 1) nodes, +1 root, we only need to count nodes of right subtree recursively.
If L != R, L must be R + 1 since the tree is complete, which means the right subtree is perfect.
It has (2^(L-1) – 1) nodes, +1 root, we only need to count nodes of left subtree recursively.

Time complexity: T(n) = T(n/2) + O(logn) = O(logn*logn)

Space complexity: O(logn)

C++

// Author: Huahua

class Solution {

public:

int countNodes(TreeNode* root) {

if (root == nullptr) return 0;

int l = depth(root->left);

int r = depth(root->right);

if (l == r)

return (1 << l) + countNodes(root->right);

else

return (1 << (l - 1)) + countNodes(root->left);

}

private:

int depth(TreeNode* root) {

if (root == nullptr) return 0;

return 1 + depth(root->left);

}

};

花花酱 LeetCode 2096. Step-By-Step Directions From a Binary Tree Node to Another

By zxi on December 5, 2021

You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.

Find the shortest path starting from node s and ending at node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

'L' means to go from a node to its left child node.
'R' means to go from a node to its right child node.
'U' means to go from a node to its parent node.

Return the step-by-step directions of the shortest path from node s to node t.

Example 1:

Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

Constraints:

The number of nodes in the tree is n.
2 <= n <= 10⁵
1 <= Node.val <= n
All the values in the tree are unique.
1 <= startValue, destValue <= n
startValue != destValue

Solution: Lowest common ancestor

It’s no hard to see that the shortest path is from the start node to the lowest common ancestor (LCA) of (start, end), then to the end node. The key is to find the LCA while finding paths from root to two nodes.

We can use recursion to find/build a path from root to a target node.
The common prefix of these two paths is the path from root to the LCA that we need to remove from the shortest path.
e.g.
root to start “LLRLR”
root to dest “LLLR”
common prefix is “LL”, after removing, it becomes:
LCA to start “RLR”
LCA to dest “LR”
Final path becomes “UUU” + “LR” = “UUULR”

The final step is to replace the L/R with U for the start path since we are moving up and then concatenate with the target path.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

string getDirections(TreeNode* root, int startValue, int destValue) {

string startPath;

string destPath;

buildPath(root, startValue, startPath);

buildPath(root, destValue, destPath);

// Remove common suffix (shared path from root to LCA)

while (!startPath.empty() && !destPath.empty()

&& startPath.back() == destPath.back()) {

startPath.pop_back();

destPath.pop_back();

}

reverse(begin(destPath), end(destPath));

return string(startPath.size(), 'U') + destPath;

}

private:

bool buildPath(TreeNode* root, int t, string& path) {

if (!root) return false;

if (root->val == t) return true;

if (buildPath(root->left, t, path)) {

path.push_back('L');

return true;

} else if (buildPath(root->right, t, path)) {

path.push_back('R');

return true;

}

return false;

}

};

花花酱 LeetCode 117. Populating Next Right Pointers in Each Node II

By zxi on November 29, 2021

Given a binary tree

struct Node {

int val;

Node *left;

Node *right;

Node *next;

}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 6000].
-100 <= Node.val <= 100

Follow-up:

You may only use constant extra space.
The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

Solution -2: Group nodes into levels

Use pre-order traversal to group nodes by levels.
Connects nodes in each level.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

Node* connect(Node* root) {

vector<vector<Node*>> levels;

dfs(root, 0, levels);

for (auto& nodes : levels)

for(int i = 0; i < nodes.size() - 1; ++i)

nodes[i]->next = nodes[i+1];

return root;

}

private:

void dfs(Node *root, int d, vector<vector<Node*>>& levels) {

if (!root) return;

if (levels.size() < d+1) levels.push_back({});

levels[d].push_back(root);

dfs(root->left, d + 1, levels);

dfs(root->right, d + 1, levels);

}

};

Solution -1: BFS level order traversal

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

Node* connect(Node* root) {

if (!root) return root;

queue<Node*> q{{root}};

while (!q.empty()) {

int size = q.size();

Node* p = nullptr;

while (size--) {

Node* t = q.front(); q.pop();

if (p)

p->next = t, p = p->next;

else

p = t;

if (t->left) q.push(t->left);

if (t->right) q.push(t->right);

}

return root;

}

};

Solution 1: BFS w/o extra space

Populating the next level while traversing current level.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

Node* connect(Node* root) {

Node* p = root;

while (p) {

Node dummy;

Node* c = &dummy;

while (p) {

if (p->left)

c->next = p->left, c = c->next;

if (p->right)

c->next = p->right, c = c->next;

p = p->next;

}

p = dummy.next;

}

return root;

}

};

花花酱 LeetCode 173. Binary Search Tree Iterator

By zxi on November 28, 2021

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:

Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output

[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); bSTIterator.next(); // return 3 bSTIterator.next(); // return 7 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 9 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 15 bSTIterator.hasNext(); // return True bSTIterator.next(); // return 20 bSTIterator.hasNext(); // return False

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
0 <= Node.val <= 10⁶
At most 10⁵ calls will be made to hasNext, and next.

Follow up:

Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

Solution: In-order traversal using a stack

Use a stack to simulate in-order traversal.

Each next, we walk to the left most (smallest) node and push all the nodes along the path to the stack.

Then pop the top one t as return val, our next node to explore is the right child of t.

Time complexity: amortized O(1) for next() call.
Space complexity: O(n)

C++

// Author: Huahua

/**

* Definition for a binary tree node.

* struct TreeNode {

* int val;

* TreeNode *left;

* TreeNode *right;

* TreeNode() : val(0), left(nullptr), right(nullptr) {}

* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}

* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}

* };

class BSTIterator {

public:

BSTIterator(TreeNode* root) : root_(root) {}

int next() {

while (root_) {

s_.push(root_);

root_ = root_->left;

}

TreeNode* t = s_.top(); s_.pop();

root_ = t->right;

return t->val;

}

bool hasNext() {

return (root_ || !s_.empty());

}

private:

TreeNode* root_;

stack<TreeNode*> s_;

};

/**

* Your BSTIterator object will be instantiated and called as such:

* BSTIterator* obj = new BSTIterator(root);

* int param_1 = obj->next();

* bool param_2 = obj->hasNext();