You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the i-th job, you have to finish all the jobs j where 0 <= j < i).
You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done in that day.
Given an array of integers jobDifficulty and an integer d. The difficulty of the i-th job is jobDifficulty[i].
Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.
Example 1:
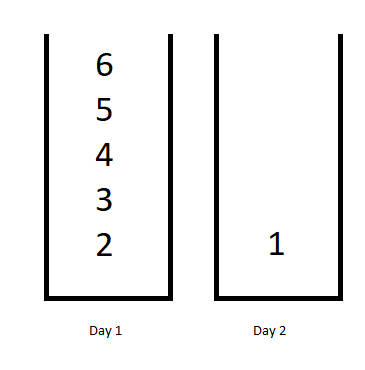
Input: jobDifficulty = [6,5,4,3,2,1], d = 2 Output: 7 Explanation: First day you can finish the first 5 jobs, total difficulty = 6. Second day you can finish the last job, total difficulty = 1. The difficulty of the schedule = 6 + 1 = 7
Example 2:
Input: jobDifficulty = [9,9,9], d = 4 Output: -1 Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.
Example 3:
Input: jobDifficulty = [1,1,1], d = 3 Output: 3 Explanation: The schedule is one job per day. total difficulty will be 3.
Example 4:
Input: jobDifficulty = [7,1,7,1,7,1], d = 3 Output: 15
Example 5:
Input: jobDifficulty = [11,111,22,222,33,333,44,444], d = 6 Output: 843
Constraints:
1 <= jobDifficulty.length <= 3000 <= jobDifficulty[i] <= 10001 <= d <= 10
Solution: DP
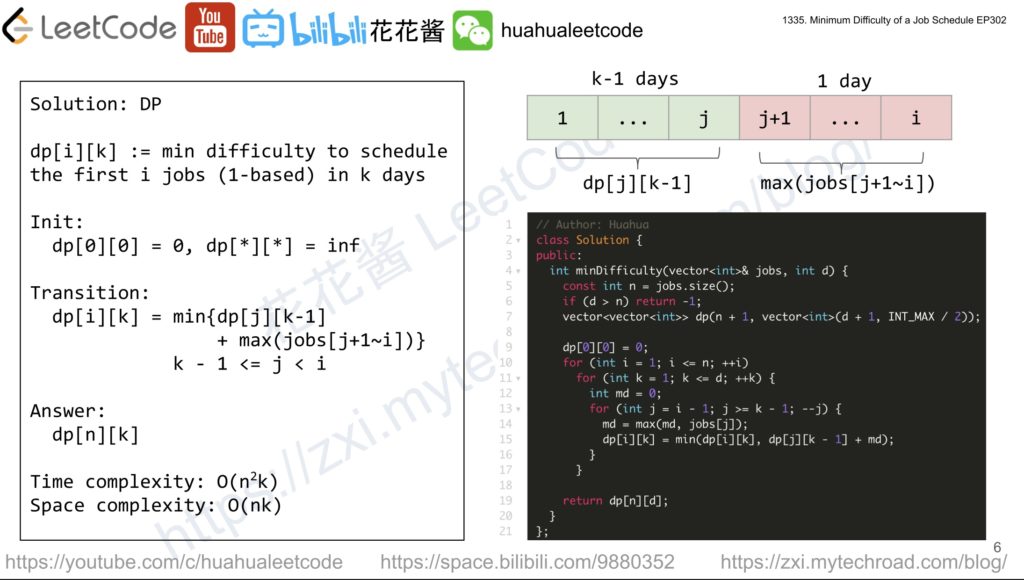
dp[i][k] := min difficulties to schedule jobs 1~i in k days.
Schedule 1 ~ j in k – 1 days and schedule j + 1 ~ i in 1 day.
Init: dp[0][0] = 0
Transition: dp[i][k] := min(dp[j][k -1] + max(jobs[j + 1 ~ i]), k – 1 <= j < i
Answer: dp[n][d]
Time complexity: O(n^2*d)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
// Author: Huahua // Author: Huahua class Solution { public: int minDifficulty(vector<int>& jobs, int d) { const int n = jobs.size(); if (d > n) return -1; vector<vector<int>> dp(n + 1, vector<int>(d + 1, INT_MAX / 2)); dp[0][0] = 0; for (int i = 1; i <= n; ++i) for (int j = i - 1, md = 0; j >= 0; --j) { md = max(md, jobs[j]); for (int k = 1; k <= min(i, d); ++k) dp[i][k] = min(dp[i][k], dp[j][k - 1] + md); } return dp[n][d]; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment