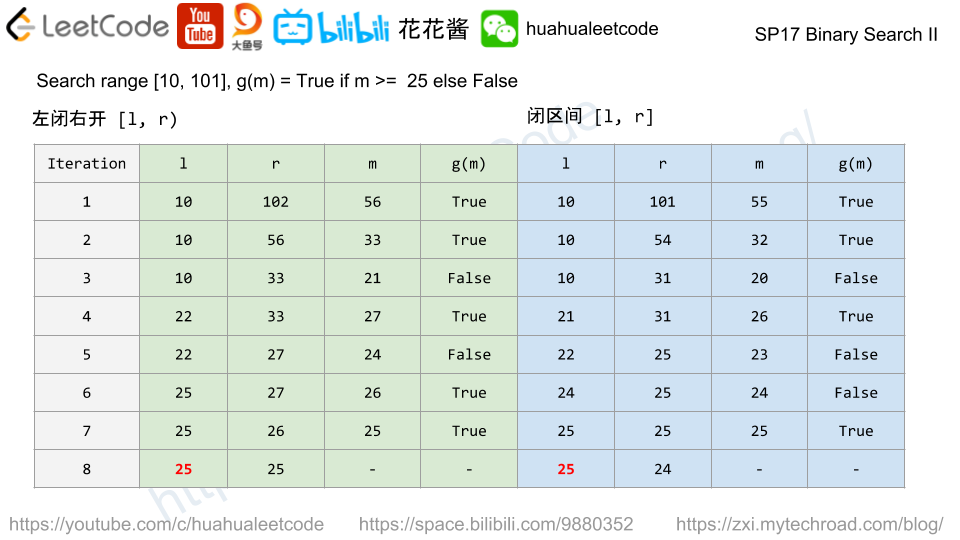
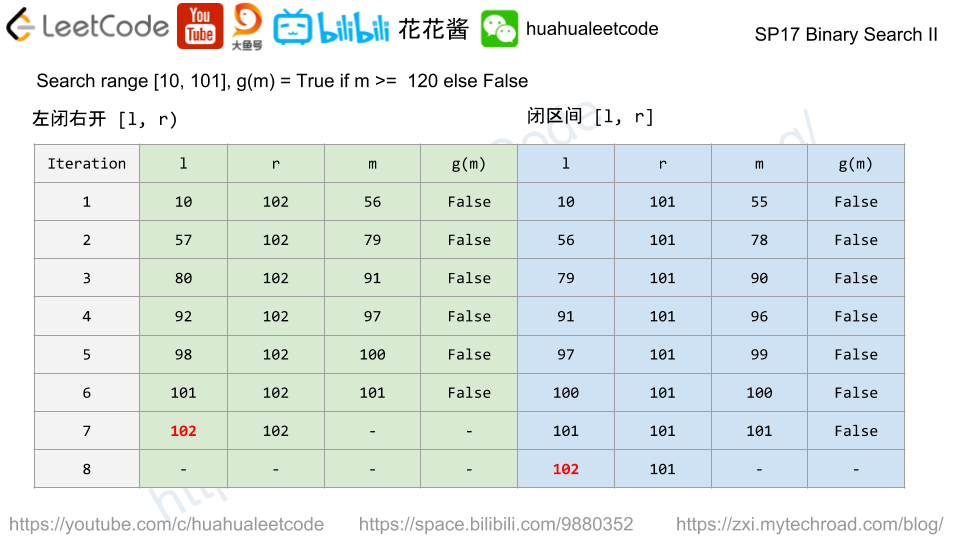
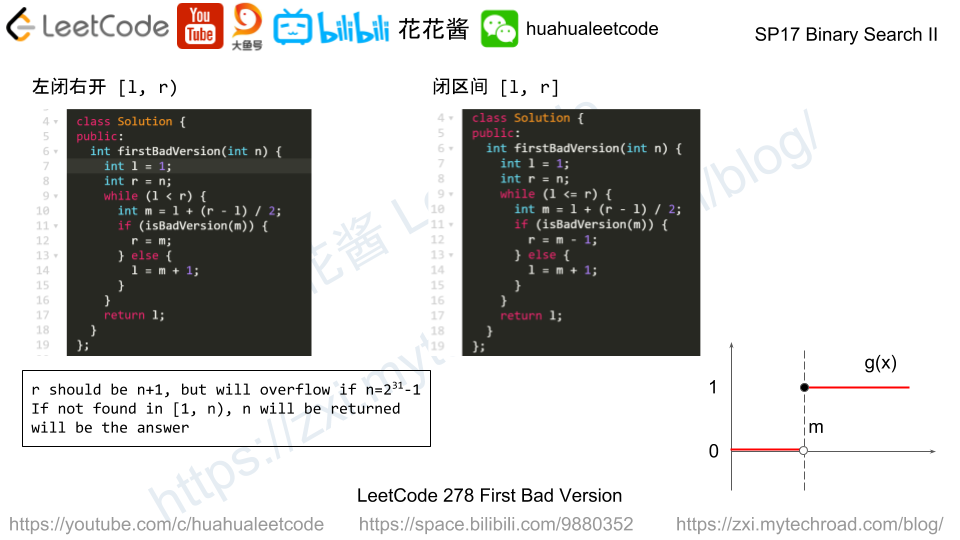
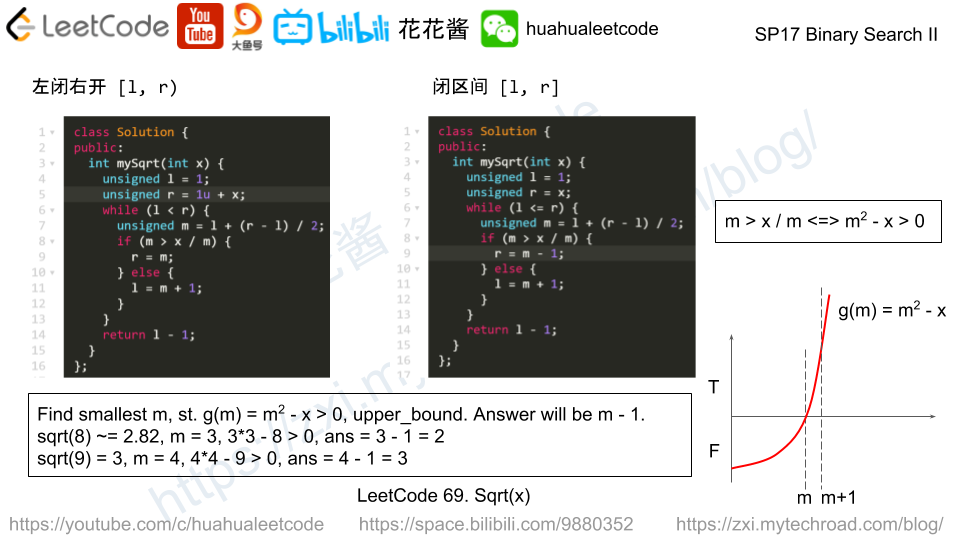
For the given function g(x) and a range [l, r] find the smallest int number m such that g(m) is True, if not found, return r + 1.
Huahua's Tech Road
Problem
https://leetcode.com/problems/count-and-say/
The count-and-say sequence is the sequence of integers with the first five terms as following:
1. 1 2. 11 3. 21 4. 1211 5. 111221
1 is read off as "one 1" or 11.11 is read off as "two 1s" or 21.21 is read off as "one 2, then one 1" or 1211.
Given an integer n where 1 ≤ n ≤ 30, generate the nth term of the count-and-say sequence.
Note: Each term of the sequence of integers will be represented as a string.
Example 1:
Input: 1 Output: "1"
Example 2:
Input: 4 Output: "1211"
Solution: Recursion + Simulation
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
// Author: Huahua, 4 ms, 8.6 MB class Solution { public: string countAndSay(int n) { string ans = "1"; for (int i = 1; i < n; ++i) ans = say(ans); return ans; } private: string say(const string& n){ string ans; int s = 0, l = n.length(); for (int e = 1; e <= l; ++e) if (e == l || n[s] != n[e]) { int count = e - s; ans += '0' + count; ans += n[s]; s = e; } return ans; } }; |
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.
Example 1:
Input: n =12Output: 3 Explanation:12 = 4 + 4 + 4.
Example 2:
Input: n =13Output: 2 Explanation:13 = 4 + 9.
Solution 1: DP
dp[i] := ans
dp[0] = 0
dp[i] = min{dp[i – j * j] + 1} 1 <= j * j <= i
dp[5] = min{
dp[5 – 2 * 2] + 1 = dp[1] + 1 = (dp[1 – 1 * 1] + 1) + 1 = dp[0] + 1 + 1 = 2,
dp[5 – 1 * 1] + 1 = dp[3] + 1 = (dp[3 – 1 * 1] + 1) + 1 = dp[1] + 2 = dp[1 – 1*1] + 1 + 2 = dp[0] + 3 = 3
};
dp[5] = 2
Time complexity: O(n * sqrt(n))
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 |
// Author: Huahua, running time: 104 ms class Solution { public: int numSquares(int n) { vector<int> dp(n + 1, INT_MAX >> 1); dp[0] = 0; for (int i = 1; i <= n; ++i) for (int j = 1; j * j <= i; ++j) dp[i] = min(dp[i], dp[i - j * j] + 1); return dp[n]; } }; |
1025. Divisor Game
Solution: Recursion with Memoization
Time complexity: O(n^2)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
// Author: Huahua, running time: 12 ms class Solution { public: bool divisorGame(int N) { cache_ = vector<int>(N + 1, -1); return canWin(N); } private: vector<int> cache_; bool canWin(int N) { if (N == 1) return false; if (cache_[N] != -1) return cache_[N]; bool win = false; for (int i = 1; i < N; ++i) if (N % i == 0) win |= !canWin(N - i); return cache_[N] = win; } }; |
1026. Maximum Difference Between Node and Ancestor
Solution: Resolution, pass min / max of ancestor nodes
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
class Solution { public: int maxAncestorDiff(TreeNode* root) { if (!root) return 0; return maxDiff(root, root->val, root->val); } private: int maxDiff(TreeNode* root, int l, int r) { if (!root) return 0; int cur = max(abs(root->val - l), abs(root->val - r)); l = min(l, root->val); r = max(r, root->val); return max(cur, max(maxDiff(root->left, l, r), maxDiff(root->right, l, r))); } }; |
1027. Longest Arithmetic Sequence
Solution 1: Brute Force + Pruning
Time complexity: O(n^3) ~ O(n^2) in practice
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
// Author: Huahua, running time: 352 ms class Solution { public: int longestArithSeqLength(vector<int>& A) { int n = A.size(); unordered_set<int> h; int ans = 2; for (int a: A) h.insert(a); for (int i = 0; i < n - 1; ++i) for (int j = i + 1; j < n; ++j) { int d = (A[j] - A[i]); int t = A[j] + d; int l = 2; if (!h.count(t)) continue; int k = j + 1; for (int k = j + 1; k < n; ++k) if (A[k] == t) { t += d; ++l; } ans = max(ans, l); } return ans; } }; |
1028. Recover a Tree From Preorder Traversal
Solution: Recursion
Check the current depth and expected depth, if don’t match, return nullptr.
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
// Author: Huahua, running time: 24 ms class Solution { public: TreeNode* recoverFromPreorder(string S) { int i = 0; return recover(S, i, 0); } private: TreeNode* recover(const string& s, int& i, int depth) { const int d = getD(s, i); if (d != depth) { i -= d; return nullptr; } auto root = new TreeNode(getVal(s, i)); root->left = recover(s, i, d + 1); root->right = recover(s, i, d + 1); return root; } int getD(const string& s, int& i) { int d = 0; while (i < s.length() && s[i] == '-') {++d; ++i;} return d; } int getVal(const string& s, int& i) { int val = 0; while (i < s.length() && isdigit(s[i])) val = val * 10 + (s[i++] - '0'); return val; } }; |
Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.
Note:
You may assume k is always valid, 1 ≤ k ≤ BST’s total elements.
Example 1:
Input: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 Output: 1
Example 2:
Input: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
Output: 3
Follow up:
What if the BST is modified (insert/delete operations) often and you need to find the kth smallest frequently? How would you optimize the kthSmallest routine?
Solution: Inorder traversal
Time complexity: O(n)
Space compleixty: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class Solution { public: int kthSmallest(TreeNode* root, int k) { return inorder(root, k); } private: int inorder(TreeNode* root, int& k) { if (!root) return -1; int x = inorder(root->left, k); if (k == 0) return x; if (--k == 0) return root->val; return inorder(root->right, k); } }; |